• [latex] m [/ latex] = [latex] r [/ latex] và [latex] n [/ latex] = [latex] s [/ latex]  tức là thứ tự của hai ma trận phải giống nhau
• Với mọi giá trị của i và j, [latex] p_ {ij} [/ latex] = [latex] q_ {ij} [/ latex] .

Nhưng có một cách khác để so sánh các ma trận. Trong trường hợp này, các ma trận  tương đương với nhau. Đối với ma trận   [latex] P [/ latex] = [latex] [p_ {ij}] _ {m × n} [/ latex] tương đương với ma trận  [latex] Q [/ latex]  =  [latex] [ q_ {ij}] _ {r × s} [/ latex] , tức là P ~ Q, hai điều kiện sau phải được thỏa mãn:

• m = r và n = s; một lần nữa, thứ tự của hai ma trận phải giống nhau

• P sẽ được chuyển thành Q bằng cách sử dụng phép biến đổi cơ bản và ngược lại.

Phép biến đổi cơ bản của ma trận là rất quan trọng. Nó được sử dụng để tìm các ma trận tương đương và cũng để tìm nghịch đảo của ma trận. Phép biến đổi cơ bản đang chơi với các hàng và cột của ma trận. Hãy cùng chúng tôi tìm hiểu cách thực hiện phép biến đổi trên ma trận.

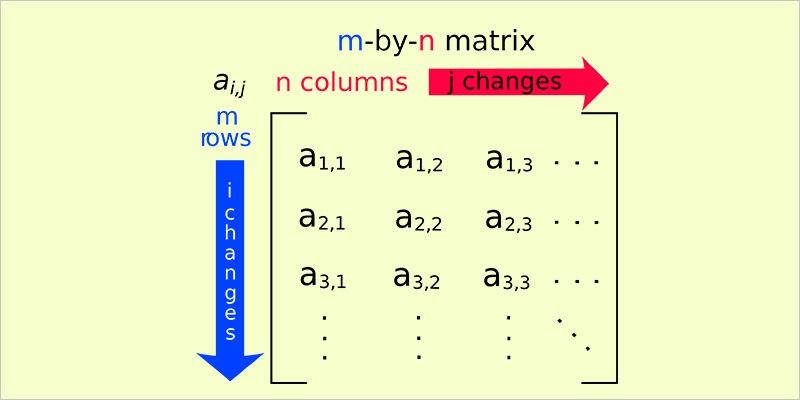
Chuyển đổi hàng sơ cấp

Như tên cho thấy, chỉ các hàng của ma trận được biến đổi và KHÔNG có thay đổi nào được thực hiện trong các cột. Các phép toán hàng này được thực hiện theo một bộ quy tắc nhất định đảm bảo rằng ma trận được biến đổi tương đương với ma trận ban đầu. Các quy tắc này là:

• Hai hàng bất kỳ có thể hoán đổi cho nhau. Sự trao đổi của các hàng [latex] i ^ {th} [/ latex] và [latex] j ^ {th} [/ latex]  được biểu diễn như sau:

[latex] R_i ↔ R_j [/ latex]

Ví dụ: If [latex] A [/ latex] = [latex]

[/ latex] , áp dụng [latex] R_1 ↔ R_3 [/ latex] , chúng tôi nhận được [latex] B [/ latex] = [latex]

[/ mủ] . Đây, A ~ B.

• Tất cả các phần tử của bất kỳ hàng nào đều có thể được nhân với bất kỳ số nào khác không. Phép nhân của hàng [latex] i ^ {th} [/ latex] với một số khác 0, được biểu diễn như sau:

[latex] R_i \ rightarrow kR_i [/ ​​latex]

Ví dụ: Nếu A = [latex]

[/ latex] , áp dụng [latex] R_2 \ rightarrow 2R_2 [/ latex] , chúng tôi nhận được [latex] B [/ latex] = [latex]

[/ mủ] . Một lần nữa, A ~ B.

• Tất cả các phần tử của một hàng có thể được thêm vào các phần tử tương ứng của một hàng khác nhân với bất kỳ hằng số khác 0. Nếu các phần tử của hàng [latex] i ^ {th} [/ latex] đang được thêm vào các phần tử của hàng [latex] j ^ {th} [/ latex]  (nhân với số khác không k), thì nó được đại diện là:

[latex] R_i \ rightarrow R_i + k R_j [/ latex]

Một điều quan trọng cần lưu ý ở đây là thay đổi sẽ chỉ phản ánh trong các phần tử của hàng [latex] i ^ {th} [/ latex]  . Các phần tử của hàng [latex] j ^ {th} [/ latex] sẽ được giữ nguyên.

Ví dụ: If [latex] A [/ latex] = [latex]

[/ latex] , áp dụng [latex] R_1 \ rightarrow R_1 + (-2) R_3 [/ latex] , chúng tôi nhận được [latex] B [/ latex] =  [latex]

[/ mủ] . Đây, A ~ B.

Thật dễ dàng để tìm ra ở đây là nếu k = 1, nó chỉ giảm để bổ sung các yếu tố của [latex] i ^ {th} [/ latex]  hàng để các yếu tố của tương ứng [latex] j ^ {th} [/ latex]  hàng . Ngoài ra, nếu k = -1, điều đó có nghĩa là trừ các phần tử của hàng [latex] j ^ {th} [/ latex]  khỏi các phần tử tương ứng của hàng [latex] i ^ {th} [/ latex]  .

Ví dụ: If [latex] P [/ latex] = [latex]

[/ latex] , áp dụng [latex] R_2 \ rightarrow R_2 + R_3 [/ latex] , chúng tôi nhận được [latex] Q [/ latex] =  [latex]

[/ mủ] . P ~ Q

Đó là ba phép toán / phép biến đổi hàng cơ bản. Các thao tác trên cột cơ bản là chính xác các thao tác được thực hiện trên các cột.

Hoạt động cột cơ bản

Ba phép toán đó cho các hàng, nếu được áp dụng cho các cột theo cùng một cách, chúng ta nhận được phép toán cột cơ bản. Như chúng ta đã thảo luận chi tiết về chuyển đổi hàng, chúng ta sẽ thảo luận ngắn gọn về chuyển đổi cột. Các quy tắc để chuyển đổi cột cơ bản là:

• Hai cột bất kỳ có thể hoán đổi cho nhau tức là [latex] C_i ↔ C_j [/ latex] .

Ví dụ: If [latex] A [/ latex] = [latex]

[/ latex] , áp dụng [latex] C_1 ↔ C_2 [/ latex] , chúng tôi nhận được [latex] B [/ latex] = [latex]

[/mủ cao su]

Đây, A ~ B. 

• Tất cả các phần tử của bất kỳ cột nào cũng có thể được nhân với bất kỳ số nào khác không, tức là [latex] C_i ↔ k C_i [/ ​​latex] .

Ví dụ: If [latex] A [/ latex] =
[latex]

[/ latex] , áp dụng [latex] C_2 \ rightarrow 3 C_2 [/ latex] , chúng tôi nhận được [latex] B [/ latex] = [latex]

[/ mủ]
. Một lần nữa, A ~ B.

• Tất cả các phần tử của một cột có thể được thêm vào các phần tử tương ứng của một cột khác nhân với bất kỳ hằng số khác 0, tức là [latex] C_i \ rightarrow C_i + k C_j [/ latex]

Ví dụ: If [latex] A [/ latex] = [latex]

[/ latex] , áp dụng [latex] C_1 \ rightarrow C_1 + 3C_3 [/ latex] , chúng tôi nhận được [latex] B [/ latex] = [latex]

[/ latex] .. Đây, A ~ B.