Biến ngẫu nhiên là gì? Xem xong 5 phút hiểu luôn.

Miền của biến ngẫu nhiên là không gian mẫu, được biểu diễn dưới dạng tập hợp các kết quả có thể có của một sự kiện ngẫu nhiên. Ví dụ, khi tung một đồng xu, chỉ có hai kết quả có thể xảy ra được thừa nhận như đầu hoặc đuôi.

Định nghĩa biến ngẫu nhiên

Biến ngẫu nhiên là một quy tắc chỉ định một giá trị số cho mỗi kết quả trong không gian mẫu . Các biến ngẫu nhiên có thể rời rạc hoặc liên tục. Một biến ngẫu nhiên được cho là rời rạc nếu nó chỉ giả định các giá trị xác định trong một khoảng thời gian. Nếu không, nó là liên tục. Chúng ta thường ký hiệu các biến ngẫu nhiên bằng các chữ cái viết hoa như X và Y. Khi X nhận các giá trị 1, 2, 3,… thì nó được cho là có một biến ngẫu nhiên rời rạc.

Là một hàm, một biến ngẫu nhiên là cần thiết để được đo lường, cho phép xác suất được gán cho một tập hợp các giá trị tiềm năng. Rõ ràng là kết quả phụ thuộc vào một số biến vật lý không thể dự đoán được. Giả sử, khi chúng ta tung một đồng xu công bằng, kết quả cuối cùng là đầu hay sấp sẽ phụ thuộc vào điều kiện vật chất có thể xảy ra. Chúng tôi không thể dự đoán kết quả nào sẽ được ghi nhận. Mặc dù có những xác suất khác như đồng xu có thể bị vỡ hoặc bị mất, nhưng việc xem xét như vậy là không thể tránh khỏi.

Biến thể

Một phương sai có thể được định nghĩa là một tổng quát của biến ngẫu nhiên. Nó có các tính chất tương tự như của các biến ngẫu nhiên mà không cần nhấn mạnh đến bất kỳ loại thử nghiệm xác suất cụ thể nào. Nó luôn tuân theo một luật xác suất cụ thể.

• Một biến thể được gọi là biến thể rời rạc khi biến thể đó không có khả năng giả định tất cả các giá trị trong phạm vi đã cho.
• Nếu phương sai có thể giả định tất cả các giá trị số được cung cấp trong toàn bộ phạm vi, thì nó được gọi là phương sai liên tục.

Các loại biến ngẫu nhiên

Như đã thảo luận trong phần giới thiệu, có hai biến ngẫu nhiên, chẳng hạn như:

• Biến ngẫu nhiên rời rạc
• Biến ngẫu nhiên liên tục

Hãy cùng tìm hiểu chi tiết các loại biến này cùng với các ví dụ phù hợp bên dưới.

Biến ngẫu nhiên rời rạc

Một biến ngẫu nhiên rời rạc chỉ có thể nhận một số hữu hạn các giá trị riêng biệt như 0, 1, 2, 3, 4,…, v.v. Các phân phối xác suất của một biến ngẫu nhiên có một danh sách xác suất so sánh với nhau của các giá trị có thể của nó được gọi là hàm xác suất tin đại chúng.

Trong một phân tích, để một người được chọn ngẫu nhiên và chiều cao của người đó được chứng minh bằng một biến ngẫu nhiên. Về mặt logic, biến ngẫu nhiên được mô tả như một hàm liên quan giữa người đó với chiều cao của người đó. Bây giờ trong mối quan hệ với biến ngẫu nhiên, nó là một phân phối xác suất cho phép tính xác suất chiều cao nằm trong bất kỳ tập hợp con nào của các giá trị có khả năng xảy ra, chẳng hạn như khả năng chiều cao nằm trong khoảng từ 175 đến 185 cm hoặc khả năng chiều cao dưới 145 hoặc lớn hơn 180 cm. Bây giờ một biến ngẫu nhiên khác có thể là tuổi của một người có thể từ 45 tuổi đến 50 tuổi hoặc dưới 40 hoặc hơn 50 tuổi.

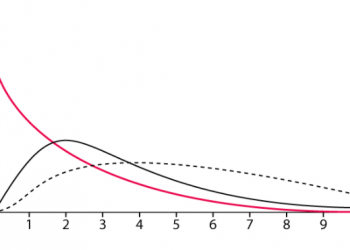
Biến ngẫu nhiên liên tục

Một biến có giá trị số được cho là liên tục nếu, trong bất kỳ đơn vị đo lường nào, bất cứ khi nào nó có thể nhận các giá trị a và b. Nếu biến ngẫu nhiên X có thể giả sử một tập giá trị vô hạn và không đếm được, thì nó được cho là một biến ngẫu nhiên liên tục. Khi X nhận một giá trị bất kỳ trong một khoảng (a, b) cho trước thì nó được coi là một biến ngẫu nhiên liên tục trong khoảng đó.

Về mặt hình thức, một biến ngẫu nhiên liên tục là một biến ngẫu nhiên có hàm phân phối tích lũy là không đổi trong suốt. Không có “khoảng cách” nào ở giữa chúng sẽ so sánh với những con số có xác suất xuất hiện hạn chế. Mặt khác, các biến này hầu như không bao giờ nhận một giá trị được quy định chính xác c nhưng có một xác suất dương là giá trị của nó sẽ dừng lại trong những khoảng thời gian cụ thể có thể rất nhỏ.

Công thức biến ngẫu nhiên

Đối với một tập hợp dữ liệu nhất định , biến ngẫu nhiên trung bình và phương sai được tính bằng công thức. Vì vậy, ở đây chúng tôi sẽ xác định hai công thức chính:

• Giá trị trung bình của biến ngẫu nhiên
• Phương sai của biến ngẫu nhiên

Giá trị trung bình của biến ngẫu nhiên: Nếu X là biến ngẫu nhiên và P là xác suất tương ứng, giá trị trung bình của một biến ngẫu nhiên được xác định bởi:

Trung bình (μ) = ∑ XP

trong đó biến X bao gồm tất cả các giá trị có thể có và P bao gồm các xác suất tương ứng.

Phương sai của biến ngẫu nhiên: Phương sai cho biết mức độ lan truyền của biến ngẫu nhiên X xung quanh giá trị trung bình là bao nhiêu. Công thức cho phương sai của một biến ngẫu nhiên được cho bởi;

Var (X) = σ ² = E (X ² ) – [E (X)] ²

trong đó E (X ² ) = ∑X ² P và E (X) = ∑ XP

Chức năng của các biến ngẫu nhiên

Đặt biến ngẫu nhiên X giả sử các giá trị x ₁ , x ₂ ,… với xác suất tương ứng P (x ₁ ), P (x ₂ ),… thì giá trị kỳ vọng của biến ngẫu nhiên được cho bởi:

Kỳ vọng của X, E (x) = ∑ x P (x).

Một biến ngẫu nhiên mới Y có thể được phát biểu bằng cách sử dụng một hàm Borel thực có thể đo lường g: R → R,  cho kết quả của một biến ngẫu nhiên có giá trị thực X. Tức là, Y = f (X). Khi đó, hàm phân phối tích lũy của Y được cho bởi:

F _Y (y) = P (g (X) ≤y)

Nếu hàm g khả nghịch (giả sử h = g ^-1  ) và đang tăng hoặc giảm, thì mối quan hệ trước đó có thể được mở rộng để có được:

Bây giờ nếu chúng ta phân biệt cả hai vế của các biểu thức trên đối với y, thì mối quan hệ giữa các hàm mật độ xác suất có thể được tìm thấy:

f _Y (y) = f _x (h (y)) | dh (y) / dy |

Biến ngẫu nhiên và phân phối xác suất

Phân phối xác suất của một biến ngẫu nhiên có thể là

• Lý thuyết liệt kê các kết quả và xác suất của các kết quả.
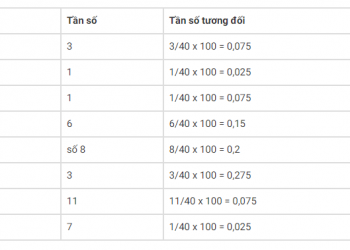
• Một danh sách thực nghiệm của các kết quả liên quan đến tần số tương đối quan sát được của chúng.
• Một danh sách chủ quan của các kết quả liên quan đến xác suất chủ quan của chúng.

Xác suất của một biến ngẫu nhiên X nhận các giá trị x được xác định là một hàm xác suất của X được ký hiệu là f (x) = f (X = x)

Phân phối xác suất luôn thỏa mãn hai điều kiện:

• f (x) ≥0
• ∑f (x) = 1

Các phân phối xác suất quan trọng là:

• Phân phối nhị thức
• Phân phối cá
• Phân phối của Bernoulli
• Phân phối hàm mũ
• Phân phối bình thường

Chuyển đổi các biến ngẫu nhiên

Việc biến đổi một biến ngẫu nhiên có nghĩa là gán lại giá trị cho một biến khác. Phép biến đổi thực sự được chèn vào để hoán đổi lại dãy số từ x thành y, sau đó hàm biến đổi là y = g (x).

Chuyển đổi của X hoặc Giá trị mong đợi của X cho một biến liên tục

Cho biến ngẫu nhiên X giả sử các giá trị x ₁ , x ₂ , x ₃ , ..… với xác suất tương ứng P (x ₁ ), P (x ₂ ), P (x ₃ ), ……… .. thì giá trị kỳ vọng của biến ngẫu nhiên được cho bởi

Kỳ vọng của X, E (x) = ∫ x P (x)

Ví dụ về biến ngẫu nhiên

Câu hỏi: Tìm giá trị trung bình của biến ngẫu nhiên liên tục, f (x) = x, 0 ≤ x ≤ 2.

Giải pháp:

Cho: f (x) = x, 0 ≤ x ≤ 2.

Công thức để tìm giá trị trung bình là E( X) =∫∞– ∞x f( x ) dx E( X) =∫20x f( x ) dx E( X)∫20x . x dx E( X)∫∞– ∞x2dx E( X) =(x33)20 E( X) = (233) – (033) E( X) = (số 83) – ( 0 ) E( X) =số 83

Do đó, giá trị trung bình của biến ngẫu nhiên liên tục, E (X) = 8/3.