- Về mặt đại số
- Số
- Trực quan
- Bằng lời nói
Mỗi người trong số họ có một số lợi thế và bất lợi. Chúng ta hãy nhìn vào chúng một lần và cố gắng hiểu chúng.
Phép cộng và phép trừ ma trận là gì? Xem xong 5 phút hiểu luôn.
Contents
Biểu diễn của một hàm – Đại số
Nó là một trong những đại diện thông thường của các chức năng. Trong điều này, các hàm được biểu diễn rõ ràng bằng cách sử dụng các công thức. Các hàm thường được biểu thị bằng các chữ cái viết thường trong bảng chữ cái. Ví dụ, chúng ta hãy lấy hàm khối lập phương.


Hình 1: Sơ đồ khối mô tả một hàm hình khối
Chữ cái tiêu chuẩn để biểu diễn hàm là f. Tuy nhiên, nó có thể được biểu diễn bằng bất kỳ biến nào. Để biểu thị hàm f về mặt đại số, tức là sử dụng công thức, chúng ta viết:
f: x→ x3
trong đó x là biến biểu thị đầu vào. Nó có thể được biểu diễn bằng bất kỳ biến nào.
x3 là công thức của hàm
f là tên của hàm
Mặc dù là một trong những cách dễ hiểu và dễ hiểu để biểu diễn một hàm, nhưng không phải lúc nào cũng dễ dàng tìm được công thức của hàm. Đối với những trường hợp đó, chúng tôi sử dụng các phương pháp biểu diễn khác.
Biểu diễn của một hàm- Trực quan
Về cơ bản, đây là biểu diễn đồ họa của các hàm. Cách biểu diễn này rất dễ hiểu. Các giá trị đầu vào được đánh dấu dọc theo trục x. Đối với bất kỳ giá trị đầu vào nào, giá trị đầu ra tương ứng là độ dịch chuyển dọc từ trục x. Ví dụ tại x = a, đầu ra bằng f (a).


Hình 2: Đồ thị của một hàm
Đồ thị biểu diễn các tính chất của các hàm số. Ví dụ: từ hình 2, chúng ta có thể trực tiếp cho biết:
- nơi biểu đồ đang tăng hoặc giảm
- nơi tỷ lệ thay đổi nhiều hơn và nơi nó ít hơn
- các giá trị cực đoan ở đâu
Do đó, đồ thị rất có lợi cho việc nghiên cứu hành vi của hàm. Một nhược điểm là chúng ta không phải lúc nào cũng có được giá trị chính xác của tất cả các kết quả đầu ra từ biểu đồ.
Biểu diễn của một hàm- Số
Về cơ bản, đây là cách biểu diễn một hàm theo dạng bảng. Bảng chứa hai cột; một với biến phụ thuộc và một với biến độc lập. Để hiển thị bằng một ví dụ, chúng ta hãy lấy một hàm f và biến độc lập là x. Bảng được đưa ra dưới dạng:
Bảng 1: Bảng biểu diễn một hàm f (x) = 2x
| x | F (x) |
| -1 | -2 |
| – 0,5 | -1 |
| 0 | 0 |
| 0,5 | 1 |
| 1 | 2 |
| 1,5 | 3 |
Mặc dù chúng ta có giá trị chính xác của các kết quả đầu ra, nhưng chúng ta chỉ có thể có một số lượng hữu hạn các kết quả đầu ra như vậy. Do đó, việc phân tích chức năng và nghiên cứu hành vi của nó trở nên khó khăn.
Biểu diễn một chức năng- Bằng lời nói
Trong cách biểu diễn hàm này, chúng ta sử dụng các từ. Ví dụ
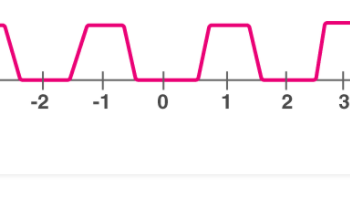
- Đối với đầu vào x, hàm cho số nguyên lớn nhất nhỏ hơn hoặc bằng x tức là hàm tầng (xem hình 3).
- Đối với đầu vào x, hàm cho giá trị bằng x tức là hàm nhận dạng (xem hình 4).


Hình 3: Chức năng tầng


Hình 4: Chức năng nhận dạng