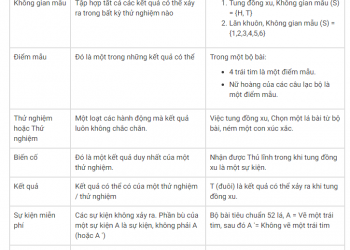
- Mẫu
- Hình thức nhân tố
- Dạng đỉnh
Nói chung, có bốn phương pháp khác nhau để giải phương trình bậc hai. Các phương pháp đó là:
- Bao thanh toán
- Sử dụng căn bậc hai
- Hoàn thành các ô vuông
- Sử dụng công thức bậc hai
Trong trang giải phương trình bậc hai này, chúng ta sẽ sử dụng công thức bậc hai để giải phương trình bậc hai.
Contents
Làm thế nào để giải phương trình bậc hai hoạt động?
Phương trình bậc hai không là gì khác ngoài một đa thức bậc 2. Căn của đa thức cho ta nghiệm của phương trình. Ở đây chúng ta phải giải một phương trình ở dạng ax 2 + bx + c = 0.
Người giải phương trình bậc hai sử dụng công thức bậc hai để tìm nghiệm nguyên của phương trình bậc hai đã cho. Quy trình sử dụng trình giải phương trình bậc hai như sau:
Bước 1: Nhập các hệ số của phương trình bậc hai “a”, “b” và “c” vào các trường đầu vào.
Bước 2: Bây giờ, nhấp vào nút “Giải phương trình bậc hai” để lấy gốc.
Bước 3: Cuối cùng, phân biệt và nghiệm nguyên của phương trình bậc hai đã cho sẽ được hiển thị trong các trường đầu ra.
Nhập các giá trị của a, b và c vào bộ giải dưới đây để giải bất phương trình bậc hai đã cho.
Các bước giải phương trình bậc hai
Đầu vào cho bộ giải phương trình bậc hai có dạng
ax 2 + bx + c = 0
Trong đó a không phải là 0, a ≠ 0
Nếu giá trị của a bằng 0 thì phương trình không phải là phương trình bậc hai.
Giải phương trình bậc hai nhận được bằng cách sử dụng công thức bậc hai:
x =– b ±b2– 4 a c√2 aThông thường, chúng tôi nhận được hai giải pháp, vì ký hiệu cộng hoặc trừ “ ± ”. Bạn cần thực hiện cả phép toán cộng và trừ.
Phần của phương trình “b 2 -4ac” được gọi là “ phân biệt ” và nó tạo ra các dạng nghiệm có thể khác nhau. Một số giải pháp khả thi là
- Trường hợp 1: Khi một phần phân biệt là dương, bạn nhận được hai giải pháp thực sự
- Trường hợp 2: Khi một phần phân biệt bằng 0, nó chỉ đưa ra một giải pháp
- Trường hợp 3: Khi một phần phân biệt là tiêu cực, bạn sẽ có các giải pháp phức tạp
Trình độ giải bậc hai giúp các em học sinh lớp 10 biết rõ về các trường hợp khác nhau liên quan đến phép phân biệt tạo ra các nghiệm khác nhau. Dưới đây là một số ví dụ về phương trình bậc hai
Ví dụ về công thức bậc hai
- Trường hợp 1: b 2 – 4ac> 0
Ví dụ 1: Xét ví dụ x 2 – 3x – 10 = 0
Cho dữ liệu: a = 1, b = -3 và c = -10
b 2 – 4ac = (-3) 2 – 4 (1) (- 10)
= 9 +40 = 49
b 2 – 4ac = 49> 0
Do đó, chúng tôi nhận được hai giải pháp thực sự
Công thức bậc hai tổng quát được cho là;
x =– b ±b2– 4 a c√2 a x =– ( – 3 ) ±( – 3)2– 4 ( 1 ) ( – 10 )√2 ( 1 ) x =3 ±9 + 40√2 x =3 ±49√2 x =3 ± 72x = 10/2, -4/2
x = 5, -2
Do đó, các nghiệm là 5 và -2
- Trường hợp 2: b 2 – 4ac = 0
Ví dụ 2: Hãy xem xét một ví dụ 9x 2 + 12x + 4 = 0
Cho dữ liệu: a = 9, b = 12 và c = 4
b 2 – 4ac = (12) 2 – 4 (9) (4)
= 144 – 144 = 0
b 2 – 4ac = 0
Do đó, chúng tôi chỉ nhận được một giải pháp riêng biệt
Công thức bậc hai tổng quát được cho là
x =– b ±b2– 4 a c√2 a x =– ( 12 ) ±( 12)2– 4 ( 9 ) ( 4 )√2 ( 9 ) x =– 12 ±144 – 144√18 x =– 12 ±0√18 x =– 1218x = -6/9 = -2/3
x = -2/3
Do đó, giải pháp là -2 / 3
- Trường hợp 3: b 2 – 4ac <0
Ví dụ 3: Xét một ví dụ x 2 + x + 12 = 0
Cho dữ liệu: a = 1, b = 1 và c = 12
b 2 – 4ac = (1) 2 – 4 (1) (12)
= 1 – 48 = -47
b 2 – 4ac = -47 <0
Do đó, chúng tôi nhận được các giải pháp phức tạp
Công thức bậc hai tổng quát được cho là
x =– b ±b2– 4 a c√2 a x =– ( 1 ) ±( 1)2– 4 ( 1 ) ( 12 )√2 ( 1 ) x =– 1 ±1 – 48√2 x =– 1 ±– 47√2 x =– 1 + i47√2 và x =– 1 – tôi47√2Do đó, các giải pháp là
x =– 1 + i47√2 và x =– 1 – tôi47√2
Các câu hỏi thường gặp về bộ giải phương trình bậc hai
Ý nghĩa của phương trình bậc hai là gì?
Trong Toán học, phương trình bậc hai được định nghĩa là phương trình đại số bậc 2 và nó phải ở dạng ax 2 + bx + c = 0. Ở đây, a, b và c là các hệ số của biến x, và giá trị của “a” không được bằng 0. (tức là, a ≠ 0). Các nghiệm của phương trình bậc hai được gọi là nghiệm của phương trình.
Bốn phương pháp khác nhau để giải phương trình bậc hai là gì?
Các phương pháp khác nhau để giải quyết các phương trình bậc hai là:
Bao thanh toán
Hoàn thành các ô vuông
Sử dụng phương pháp căn bậc hai
bậc thức
Phân biệt đối xử là gì?
Phép phân biệt D = b 2 – 4ac cho thấy bản chất của các nghiệm thức mà phương trình có. Nó được xác định từ các hệ số của phương trình.
Nếu D = 0, các căn bằng nhau, thực và hữu tỉ
Nếu D> 0, và cũng là một bình phương hoàn hảo, căn là thực, phân biệt và hữu tỉ
Nếu D> 0, nhưng không phải là một bình phương hoàn hảo, căn là thực, phân biệt và không hợp lý
Dạng chuẩn của phương trình bậc hai là gì?
Dạng chuẩn để biểu diễn phương trình bậc hai là
Ax 2 + Bx + C = 0
Ở đây A, B và C là các giá trị đã biết, và A không được bằng 0.
X là một biến.
Đề cập đến các ứng dụng của phương trình bậc hai.
Phương trình bậc hai được sử dụng trong các hoạt động đời sống hàng ngày như tìm lợi nhuận của sản phẩm, tính diện tích của căn phòng, điền kinh, tìm tốc độ của vật thể, v.v.
Xem thêm:
| Biểu diễn các con số ở dạng chung là gì? Xem xong 5 phút hiểu luôn. |
| Biểu diễn của một chức năng là gì? Xem xong 5 phút hiểu luôn. |
| Tần số tương đối là gì? Xem xong 5 phút hiểu luôn. |