Các ứng dụng của lượng giác, xem xong hiểu luôn.

Các ứng dụng của lượng giác

Lượng giác có thể được định nghĩa là các phép tính với các tam giác liên quan đến việc nghiên cứu độ dài, chiều cao và góc. Lượng giác và các chức năng của nó có rất nhiều ứng dụng trong cuộc sống hàng ngày của chúng ta. Ví dụ, nó được sử dụng trong địa lý để đo khoảng cách giữa các điểm mốc, trong thiên văn học để đo khoảng cách của các ngôi sao gần đó và cả trong hệ thống định vị vệ tinh.

Trước khi đi vào phần giải chi tiết các ứng dụng của lượng giác, chúng ta hãy bắt đầu với phần giới thiệu về lượng giác và các chức năng của nó.

Lượng giác là gì?

Lượng giác là một nghiên cứu về mối quan hệ của góc, độ dài và chiều cao. Nó xuất hiện vào thế kỷ thứ ba trước Công nguyên liên quan đến các ứng dụng từ thiên văn học đến nghiên cứu hình học. Giờ đây, nó đã phổ biến các ứng dụng của mình sang các lĩnh vực rộng lớn hơn như kỹ thuật, vật lý, khảo sát, kiến ​​trúc, thiên văn học và thậm chí trong điều tra hiện trường vụ án.

Ngoài thiên văn và địa lý, lượng giác có thể áp dụng trong nhiều lĩnh vực khác nhau như định vị vệ tinh, phát triển âm nhạc máy tính, lý thuyết số hóa học, hình ảnh y tế, điện tử, kỹ thuật điện, kỹ thuật dân dụng, kiến ​​trúc, kỹ thuật cơ khí, hải dương học, địa chấn học, ngữ âm, nén hình ảnh và trò chơi phát triển.

Ứng dụng lượng giác trong cuộc sống thực

Nó có thể không có ứng dụng trực tiếp trong việc giải quyết các vấn đề thực tế nhưng được sử dụng trong nhiều lĩnh vực khác nhau. Ví dụ, lượng giác được sử dụng để phát triển âm nhạc máy tính: như bạn đã quen thuộc rằng âm thanh truyền đi dưới dạng sóng và dạng sóng này, thông qua một hàm sin hoặc cosine để phát triển âm nhạc máy tính. Dưới đây là một vài ứng dụng có thể áp dụng lượng giác và các chức năng của nó.

Lượng giác để đo chiều cao của một tòa nhà hoặc một ngọn núi

Lượng giác được sử dụng để đo chiều cao của một tòa nhà hoặc một ngọn núi. Khoảng cách của một tòa nhà từ điểm nhìn và góc nâng có thể dễ dàng xác định chiều cao của tòa nhà bằng cách sử dụng các hàm lượng giác .

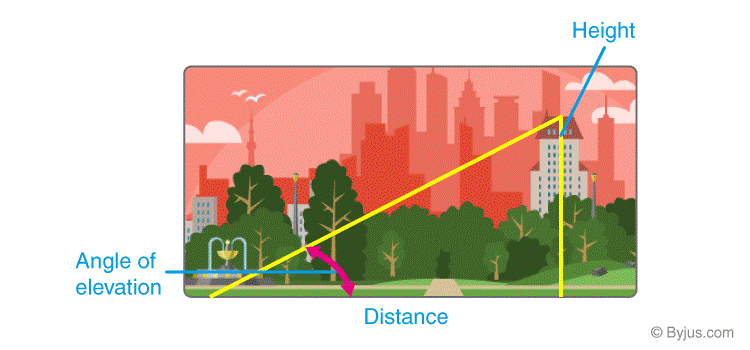
Thí dụ:

Nếu khoảng cách từ nơi quan sát được tòa nhà là 90 ft tính từ chân đế và góc nâng đến đỉnh của tòa nhà là 35 °, thì hãy tìm chiều cao của tòa nhà.

Giải pháp:

Được:

1. Khoảng cách từ tòa nhà là 90 feet từ cơ sở của nó.
2. Góc nâng từ đỉnh của tòa nhà là 35 ° .

Chúng ta hãy tìm chiều cao của tòa nhà bằng cách nhớ lại các công thức lượng giác. Ở đây, góc và độ dài cạnh liền kề được cung cấp. Vì vậy, bằng cách sử dụng công thức củarám nắng.

rám nắng35∘=O p p o s i t eStôi deA dj a c e n tStôi de

tan 35 ° =  h / 90

h  =  90  ×  tan 35 °

h  =  90  ×  0,7002

h  = 63.018  f t

Như vậy, chiều cao của tòa nhà là 63,018  f t .

Tìm hiểu thêm: Chiều cao và khoảng cách như một ứng dụng của lượng giác

Lượng giác trong hàng không

Công nghệ hàng không đã phát triển với nhiều nâng cấp trong vài năm gần đây. Nó đã tính đến tốc độ, hướng và khoảng cách cũng như tốc độ và hướng của gió. Gió đóng một vai trò quan trọng trong thời gian và cách thức một chuyến bay sẽ di chuyển. Phương trình này có thể được giải bằng cách sử dụng lượng giác.

For example, if an aeroplane is travelling at 250 miles per hour, 55 ° of the north of east and the wind blowing due to south at 19 miles per hour. Phép tính này sẽ được giải bằng cách sử dụng lượng giác và tìm cạnh thứ ba của tam giác sẽ dẫn máy bay đi đúng hướng.

Lượng giác trong Tội phạm học

Lượng giác thậm chí còn được sử dụng trong điều tra hiện trường vụ án. Các hàm lượng giác rất hữu ích để tính toán quỹ đạo của một viên đạn và ước tính nguyên nhân của một vụ va chạm trong một vụ tai nạn ô tô. Hơn nữa, nó được sử dụng để xác định cách một vật thể rơi xuống hoặc súng được bắn ở góc độ nào.

Lượng giác trong sinh học biển

Lượng giác thường được các nhà sinh học biển sử dụng để đo đạc nhằm tìm ra độ sâu của ánh sáng mặt trời ảnh hưởng đến quá trình quang hợp của tảo. Sử dụng hàm lượng giác và các mô hình toán học, các nhà sinh học biển ước tính kích thước của các loài động vật lớn hơn như cá voi và cũng hiểu được hành vi của chúng.

Lượng giác trong Điều hướng

Lượng giác được sử dụng trong việc định hướng các hướng; nó ước tính đặt la bàn theo hướng nào để có được phương hướng thẳng. Với sự trợ giúp của la bàn và các chức năng lượng giác trong điều hướng, sẽ dễ dàng xác định vị trí và cũng có thể tìm khoảng cách cũng như nhìn thấy đường chân trời.

Các ứng dụng khác của lượng giác

• Giải tích dựa trên lượng giác và đại số
• Các hàm lượng giác cơ bản như sin và cosine được sử dụng để mô tả sóng âm thanh và ánh sáng
• Lượng giác được sử dụng trong hải dương học để tính toán độ cao của sóng và thủy triều trong đại dương
• Nó được sử dụng trong việc tạo bản đồ
• Nó được sử dụng trong các hệ thống vệ tinh

Như vậy, ở đây chúng ta đã thảo luận về Lượng giác và tầm quan trọng của nó cùng với những ứng dụng của ngành Toán học này trong đời sống hàng ngày, điều mà mọi học sinh chuyên Toán đều mong muốn được biết.

Xem thêm: 

• Tỷ lệ nghịch là gì? xem xong 5 phút hiểu luôn.
• Quy tắc bệnh viện L là gì? Xem xong 5 phút hiểu luôn.

  Tích phân là gì? Xem xong 5 phút hiểu luôn.