x + 2 y≤ 100
x + 2 y≤ 70
x ≥ 0 , y
Bước 1: Trong các phương trình trên, chúng ta có thể thấy rằng x ≥ 0 và
Y≥ 0, do đó chúng tôi sẽ chỉ tập trung vào góc phần tư thứ nhất.
Bước 2: Chúng ta hãy vẽ phương trình tuyến tính x + 2y = 100 bằng cách vẽ hai điểm (0,50) và (100,0) & x + y = 70 bằng cách vẽ biểu đồ các điểm (70,0) và (0,70 ).

Khi bạn vẽ biểu đồ với tất cả các ràng buộc đã cho, mục đích là xác định Vùng khả thi. Vùng khả thi là vùng chung được xác định bởi tất cả các ràng buộc đã cho trong bài toán lập trình tuyến tính. Trong bài toán trên, vùng khả thi được hiển thị như sau: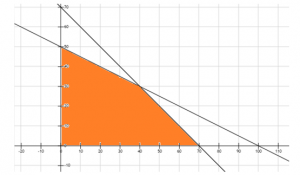

Mỗi và mọi điểm nằm trong vùng khả thi là lựa chọn khả thi và sẽ thỏa mãn tất cả các điều kiện đã cho. Bất kỳ điểm nào nằm ngoài vùng khả thi đã cho là một giải pháp không khả thi và sẽ không thỏa mãn đồng thời tất cả các điều kiện.
Sau khi vẽ đồ thị trên, chúng ta biết khoảng x và y thỏa mãn tất cả các điều kiện cho trước. Giải pháp đồ họa cũng có thể được sử dụng để tìm ra giải pháp tối ưu của bài toán trên. Bất kỳ điểm nào trong vùng khả thi cho giá trị lớn nhất hoặc nhỏ nhất của hàm mục tiêu được gọi là một giải pháp tối ưu. Trong vùng khả thi, chúng ta có thể thấy rằng có vô số điểm thỏa mãn đồng thời các ràng buộc đã cho. Nhưng làm thế nào chúng ta sẽ nhận được giá trị lớn nhất hoặc nhỏ nhất của hàm mục tiêu Z = 40x + 15y?
Để tìm ra giải pháp tối ưu, chúng ta tuân theo các định lý dưới đây:
Định lý 1: Gọi R là vùng khả thi của bài toán lập trình tuyến tính và cho Z = Ax + By là hàm mục tiêu. Khi đó giá trị tối ưu (lớn nhất hoặc nhỏ nhất) của Z sẽ xảy ra tại một điểm góc (đỉnh) của vùng khả thi, với điều kiện tồn tại giá trị tối ưu của Z và tại đó các biến x và y chịu các ràng buộc được mô tả bởi bất đẳng thức tuyến tính.
Định lý 2: Gọi R là vùng khả thi của một bài toán lập trình tuyến tính và gọi Z = Ax + By là hàm mục tiêu. Nếu R là giới hạn thì Z có cả giá trị lớn nhất và giá trị nhỏ nhất trên R và mỗi giá trị này xảy ra tại một điểm góc (đỉnh) của R.
Nếu R là không giới hạn thì giá trị lớn nhất và nhỏ nhất của Z có thể không tồn tại, nhưng nếu tồn tại thì nó sẽ xảy ra tại điểm góc của vùng R.
Trong bài toán lập trình tuyến tính trên, các điểm góc là (0,0), (70,0), (40,30) và (0,50)
Thay các giá trị trên vào hàm mục tiêu Z = 40x + 15y ta được ,
Z = 0 cho (0,0)
Z = 2800 cho (70,0)
Z = 2050 cho (40,30)
Z = 750 cho (0,50)
Do đó giá trị lớn nhất của Z xảy ra tại (70,0) và giá trị nhỏ nhất của Z xảy ra tại (0,0).
Xem thêm: