Cách tìm tâm đường tròn ngoại tiếp đơn giản

Trung tâm của một Tam giác là gì?

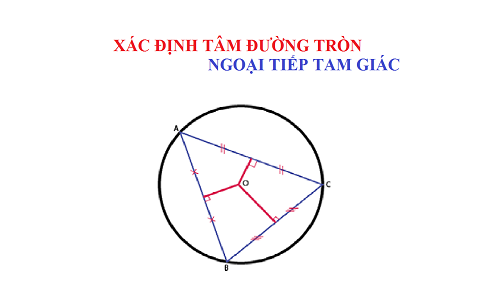
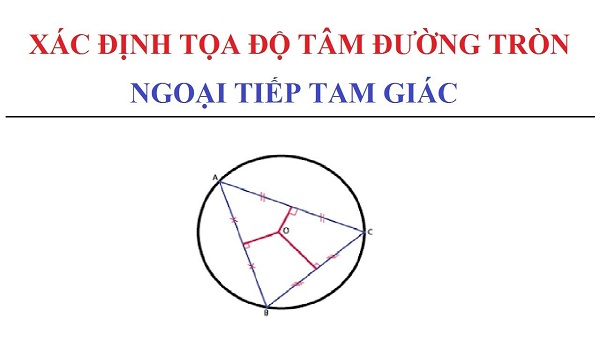
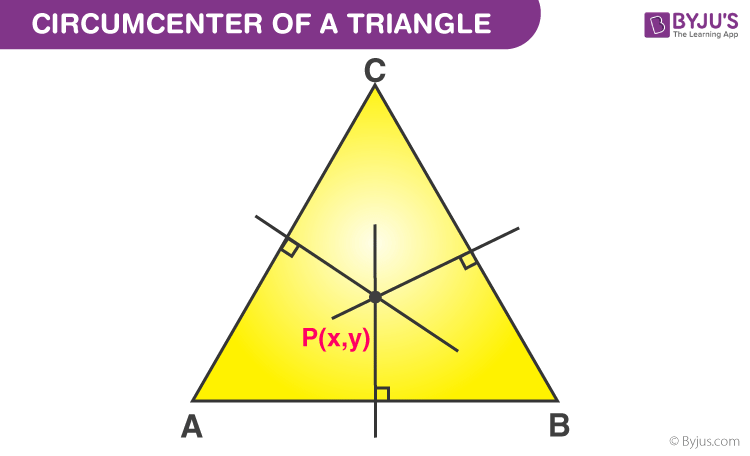
Đường tròn của một tam giác được định nghĩa là điểm mà các đường phân giác trung trực của các cạnh của tam giác cụ thể đó cắt nhau. Nói cách khác, điểm đồng quy của đường phân giác các cạnh của một tam giác được gọi là đường tròn ngoại tiếp. Nó được ký hiệu là P (X, Y). Đường tròn ngoại tiếp cũng là tâm của đường tròn ngoại tiếp tam giác đó và nó có thể nằm trong hoặc ngoài tam giác.

Công thức Circumcenter

Đây,

• A (x ₁ , y ₁ ), B (x ₂ , y ₂ ) và C (x ₃ , y ₃ ) là các đỉnh của tam giác và A, B, C là các góc tương ứng của chúng.

Phương pháp tính đường tròn tâm của tam giác

Các bước để tìm đường tròn ngoại tiếp tam giác là:

• Tính trung điểm của các tọa độ đã cho, tức là trung điểm của AB, AC và BC
• Tính độ dốc của một đường cụ thể
• Bằng cách sử dụng trung điểm và hệ số góc, hãy tìm phương trình của đường thẳng (yy ₁ ) = m (xx ₁ )
• Tìm ra phương trình của đường thẳng kia theo cách tương tự
• Giải phương trình hai đường phân giác bằng cách tìm giao điểm
• Giao điểm được tính toán sẽ là đường tròn của tam giác đã cho

Tìm đường tròn bằng phương trình tuyến tính

Đường tròn cũng có thể được tính bằng cách lập phương trình tuyến tính sử dụng công thức khoảng cách. Chúng ta hãy lấy (X, Y) là tọa độ của đường tròn ngoại tiếp. Theo tính chất của đường tròn, khoảng cách của (X, Y) từ mỗi đỉnh của một tam giác sẽ như nhau.

Giả sử rằng D1 là khoảng cách giữa đỉnh (x ₁ , y ₁ ) và đường tròn (X, Y), sau đó công thức được cho bởi,

D ₁ = √ [(X − x ₁ ) ² + (Y − y ₁ ) ² ]

D ₂ = √ [(X − x ₂ ) ² + (Y − y ₂ ) ² ]

D ₃ = √ [(X − x ₃ ) ² + (Y − y ₃ ) ² ]

Tìm hiểu thêm: Khoảng cách giữa hai điểm

Bây giờ, vì D ₁ = D ₂ và D ₂ = D ₃ , chúng ta nhận được

(X − x ₁ ) ² + (Y − y ₁ ) ² = (X − x ₂ ) ² + (Y − y ₂ ) ²

Từ đó thu được hai phương trình tuyến tính. Bằng cách giải các phương trình tuyến tính bằng phương pháp thay thế hoặc loại bỏ, tọa độ của đường tròn có thể thu được.

Thuộc tính của Circumcenter

Một số tính chất của đường tròn ngoại tiếp tam giác như sau:

• Đường tròn ngoại tiếp là tâm của đường tròn ngoại tiếp
• Tất cả các đỉnh của một tam giác đều cách đều với đường tròn ngoại tiếp
• Trong một tam giác có góc nhọn, đường tròn nằm bên trong tam giác
• Trong một tam giác có góc tù, nó nằm bên ngoài của tam giác
• Đường tròn nằm ở trung điểm cạnh huyền của tam giác vuông

Làm thế nào để xây dựng hình tròn của một tam giác?

Đường tròn ngoại tiếp của bất kỳ tam giác nào có thể được xây dựng bằng cách vẽ đường phân giác vuông góc của hai cạnh bất kỳ của tam giác đó. Các bước để tạo đường tròn ngoại tiếp là:

• Bước 1: Vẽ đường phân giác vuông góc của hai cạnh bất kỳ của tam giác đã cho.
• Bước 2: Dùng thước kẻ, kéo dài các đường phân giác vuông góc cho đến khi chúng cắt nhau.
• Bước 3: Đánh dấu giao điểm là P sẽ là đường tròn ngoại tiếp tam giác. Cần lưu ý rằng, ngay cả đường phân giác của cạnh thứ ba cũng sẽ cắt nhau tại P.

Tìm hiểu thêm:

• Xây dựng hình tam giác
• Xây dựng tam giác với chu vi và hai góc của nó

Câu hỏi Ví dụ Sử dụng Công thức Vòng tròn

Câu hỏi: Tìm tọa độ đường tròn ngoại tiếp tam giác ABC với các đỉnh A = (3, 2), B = (1, 4) và C = (5, 4)?

Giải pháp:

• Phương pháp 1:

Gọi, (x, y) là tọa độ của đường tròn.

D ₁ là khoảng cách từ đường tròn ngoại tiếp đến đỉnh A

D ₂ là khoảng cách từ đường tròn ngoại tiếp đến đỉnh B

D ₃ là khoảng cách từ đường tròn ngoại tiếp đến đỉnh C

Cho: (x ₁ , y ₁ ) = (3, 2); (x ₂ , y ₂ ) = (1, 4) và (x ₃ , y ₃ ) = (5, 4)

Sử dụng công thức khoảng cách, chúng tôi nhận được

D ₁ = √ [(X − x ₁ ) ² + (Y − y ₁ ) ² ]

D ₂ = √ [(X − x ₂ ) ² + (Y − y ₂ ) ² ]

D ₃ = √ [(X − x ₃ ) ² + (Y − y ₃ ) ² ]

Vì D ₁ = D ₂ = D ₃ .

D ₁ = D ₂ cho,

(x – 3) ²  + (y – 2) ²  = (x – 1) ²  + (y – 4) ²

⇒ x ²  – 6x + 9 + y ²  + 4 – 4y = x ²  + 1 – 2x + y ²  – 8y + 16

⇒ -6x – 4y + 13 = -2x – 8y + 17

⇒ -4x + 4y = 4

⇒ -x + y = 1 ———– (1)

D ₁ = D ₃ cho,

(x – 3) ² + (y – 2) ²  = (x – 5) ²  + (y – 4) ²

⇒ x ²  – 6x + 9 + y ²  + 4 – 4y = x ²  + y ²  – 10x – 8y + 25 + 16

⇒ -6x – 4y + 13 = -10x – 8y + 41

⇒ 4x + 4y = 28

Hoặc, x + y = 7 ————– (2)

Bằng cách giải phương trình (1) và (2), chúng ta nhận được

2y = 8

Hoặc, y = 4

Bây giờ, thay y = 4 vào phương trình (1),

⇒ -x + 4 = 1

⇒ -x = 1 – 4

⇒ -x = -3

Hoặc, x = 3

Do đó, đường tròn ngoại tiếp tam giác là (x, y) = (3, 4)

• Phương pháp 2:

Các điểm đã cho là,

A = (3, 2),

B = (1, 4),

C = (5, 4)

Để tìm đường tròn, chúng ta phải giải phương trình hai đường phân giác bất kỳ và tìm giao điểm.

Vậy, trung điểm của AB = [(3 + 1) / 2, (2 + 4) / 2] = (2, 3)

Hệ số góc của AB = [(4−2) / (1−3)] = -1

Hệ số góc của đường phân giác là nghịch đảo âm của hệ số góc đã cho.

Vì vậy, hệ số góc của đường phân giác = 1

Phương trình của AB có hệ số góc 1 và tọa độ (2, 3) là,

(y – 3) = 1 (x – 2)

x – y = -1 ……………… (1)

Tương tự, đối với AC

Điểm giữa của AC = [(3 + 5) / 2, (2 + 4) / 2] = (4, 3)

Độ dốc của AC = [(4−2) / (5−3)] = 1

Hệ số góc của đường phân giác là nghịch đảo âm của hệ số góc đã cho.

Vì vậy, hệ số góc của đường trung trực = -1

Phương trình của AC có hệ số góc -1 và tọa độ (4, 3) là,

(y – 3) = -1 (x – 4)

y – 3 = -x + 4

x + y = 7 ……………… (2)

Bằng cách giải phương trình (1) và (2),

(1) + (2) ⇒ 2x = 6;

Hoặc, x = 3

Thay giá trị của x thành (1)

3 – y = -1

y = 3 + 1 = 4

Như vậy, đường tròn ngoại tiếp là (3, 4).