Định nghĩa chức năng nhận dạng
Gọi R là tập các số thực. Do đó, hàm có giá trị thực f: R → R theo y = f (a) = a với mọi a ∈ R, được gọi là hàm đồng nhất. Ở đây miền và phạm vi (miền đồng) của hàm f là R. Do đó, mỗi phần tử của tập R có một ảnh trên chính nó. Đồ thị là một đường thẳng và nó đi qua gốc tọa độ. Ứng dụng của chức năng này có thể được nhìn thấy trong ma trận nhận dạng .
Về mặt toán học, nó có thể được biểu thị bằng;
| f (a) = a ∀ a ∈ R |
Trong đó a là phần tử của tập R.
Ví dụ, f (2) = 2 là một hàm đồng nhất.
Trong lý thuyết tập hợp , khi một hàm được mô tả như một loại quan hệ nhị phân cụ thể, thì hàm đồng nhất được cho bởi quan hệ đồng nhất hoặc đường chéo của A, trong đó A là một tập hợp.
Đồ thị hàm nhận dạng
Nếu chúng ta vẽ một đồ thị cho hàm nhận dạng, thì nó sẽ có vẻ là một đường thẳng. Chúng ta hãy vẽ một đồ thị cho hàm số f (x) = x, bằng cách đặt các giá trị khác nhau của x.
| x | -2 | -1 | 0 | 1 | 2 |
| f (x) = y | -2 | -1 | 0 | 1 | 2 |
Bây giờ như bạn có thể thấy từ bảng trên, các giá trị đều giống nhau cho cả trục x và trục y. Do đó, chúng ta hãy vẽ biểu đồ dựa trên các giá trị này.
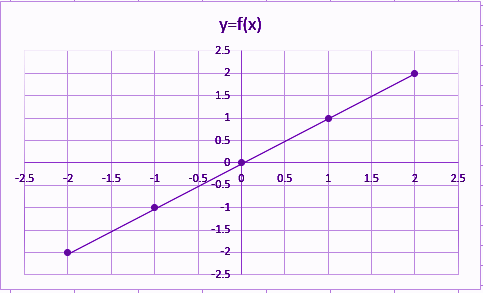

Vì vậy, từ đồ thị trên, rõ ràng là hàm số đồng dạng cho một đường thẳng trong mặt phẳng xy.
Hãy để chúng tôi giải quyết một số ví dụ dựa trên khái niệm này.
Ví dụ về chức năng nhận dạng
H.1: Chứng minh f (2x) = 2x là một hàm đồng dạng.
Lời giải: Cho trước, f (2x) = 2x
Hãy để chúng tôi đặt các giá trị của x trong hàm đã cho.
Nếu x = 1, thì;
f (2 (1)) = 2 (1) ⇒ f (2) = 2
Nếu x = 2, thì;
f (2 (2)) = 2 (2) ⇒ f (4) = 4
Nếu x = 3 thì;
f (2 (3)) = 2 (3) ⇒ f (6) = 6
Nếu x = 0, thì;
f (2 (0)) = 2 (0) ⇒ f (0) = 0
Hãy để chúng tôi thử với một số giá trị âm của x.
Nếu x = -1 thì;
f (2 (-1)) = 2 (-1) ⇒ f (-2) = -2
Nếu x = -2 thì;
f (2 (-2)) = 2 (-2) ⇒ f (-4) = -4
Nếu x = -3 thì;
f (2 (-3)) = 2 (-3) ⇒ f (-6) = -6
Chúng ta hãy vẽ một bảng cho tất cả các giá trị của x.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = f (x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
Hãy để chúng tôi vẽ biểu đồ cho các giá trị này.
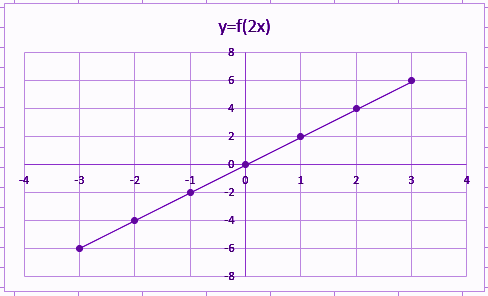

Bạn có thể thấy từ biểu đồ trên. Hàm f (2x) = 2x vẽ một đường thẳng, do đó nó là một hàm đồng nhất.
Thuộc tính của chức năng nhận dạng
- Nó là một toán tử tuyến tính trong trường hợp ứng dụng của không gian vectơ.
- Đối với số nguyên dương, nó là một hàm nhân.
- Đối với không gian vectơ m chiều, nó được biểu diễn dưới dạng ma trận nhận dạng I m .
- Trong không gian tôpô, hàm này luôn liên tục.