Giá trị tuyệt đối – Thuộc tính & Ví dụ đơn giản nhất
1 Tháng Ba, 2021Giá trị tuyệt đối là gì? Giá trị tuyệt đối đề cập đến khoảng cách của một điểm từ...
Contents
Dãy số là một công cụ toán học rất quan trọng để kiểm tra trí thông minh của một người. Các bài toán về dãy số thường gặp trong hầu hết các kỳ thi năng khiếu quản lý.
Các bài toán dựa trên một mẫu số được điều chỉnh bởi một quy tắc logic. Ví dụ: bạn có thể được yêu cầu dự đoán số tiếp theo trong một chuỗi nhất định theo quy tắc đã đặt.
Ba câu hỏi phổ biến trong kỳ thi này, có thể được hỏi, là:


Dãy số là một tiến trình hoặc một danh sách có thứ tự các số được điều chỉnh bởi một mẫu hoặc quy tắc. Các số trong một dãy được gọi là số hạng. Một dãy tiếp tục vô thời hạn mà không kết thúc được gọi là dãy vô hạn, trong khi dãy có kết thúc được gọi là dãy hữu hạn.
Các bài toán số logic thường bao gồm một hoặc hai số còn thiếu và 4 số hạng hiển thị trở lên.
Đối với trường hợp này, một nhà thiết kế thử nghiệm tạo ra một trình tự mà chỉ một trình tự phù hợp với số. Bằng cách học hỏi và vượt trội về dãy số, một cá nhân có thể rèn giũa khả năng suy luận số của mình, điều này giúp ích rất nhiều cho các hoạt động hàng ngày của chúng ta như tính thuế, cho vay hoặc kinh doanh. Đối với trường hợp này, điều quan trọng là phải học và thực hành dãy số.
ví dụ 1
Danh sách các số nào tạo thành một dãy?
Giải pháp
Danh sách các số đầu tiên không tạo thành một chuỗi vì các số thiếu thứ tự hoặc mẫu thích hợp.
Danh sách còn lại là một chuỗi vì có thứ tự thích hợp để lấy số đứng trước. Số liên tiếp nhận được bằng cách thêm 3 vào số nguyên trước đó.
Ví dụ 2
Tìm các số hạng còn thiếu trong dãy sau:
8, _, 16, _, 24, 28, 32
Giải pháp
Để tìm mô hình của điều này, trình tự, ba số liên tiếp 24, 28 và 32 được kiểm tra và quy tắc thu được. Bạn có thể nhận thấy rằng, số tương ứng có được bằng cách thêm 4 vào số đứng trước.
Do đó, các số hạng còn thiếu là: 8 + 4 = 12 và 16 + 4 = 20
Ví dụ 3
Giá trị của n là bao nhiêu trong dãy số sau?
12, 20, n , 36, 44,
Giải pháp
Xác định mẫu của dãy số bằng cách tìm hiệu giữa hai số hạng liên tiếp.
44 – 36 = 8 và 20 – 12 = 8.
Do đó, mẫu của dãy là phép cộng 8 vào số hạng đứng trước.
Vì thế,
n = 20 + 8 = 28.
Có nhiều dãy số, nhưng dãy số học và dãy hình học là những dãy số thường được sử dụng nhất. Hãy xem từng cái một.
Đây là một loại dãy số trong đó số hạng tiếp theo được tìm thấy bằng cách thêm một giá trị không đổi vào số trước của nó. Khi số hạng đầu tiên, được ký hiệu là x 1 và d là hiệu chung giữa hai số hạng liên tiếp, dãy số được tổng quát theo công thức sau:
x n = x 1 + (n-1) d
Ở đâu;
x n là n thứ hạn
x 1 là số hạng đầu tiên, n là số số hạng và d là hiệu chung giữa hai số hạng liên tiếp.
Ví dụ 4
Bằng cách lấy ví dụ về dãy số: 3, 8, 13, 18, 23, 28 ……
Hiệu số chung được tìm thấy là 8 – 3 = 5;
Số hạng đầu tiên là 3. Ví dụ, để tìm số hạng thứ 5 bằng công thức số học; Thay các giá trị của số hạng đầu tiên là 3, hiệu chung là 5 và n = 5
Số hạng thứ 5 = 3 + (5-1) 5
= 23
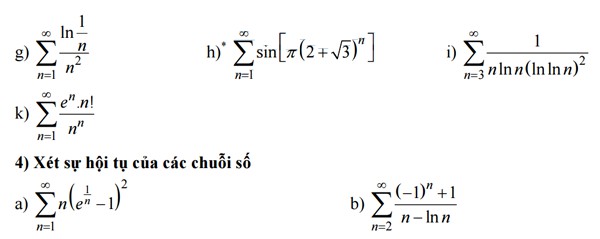
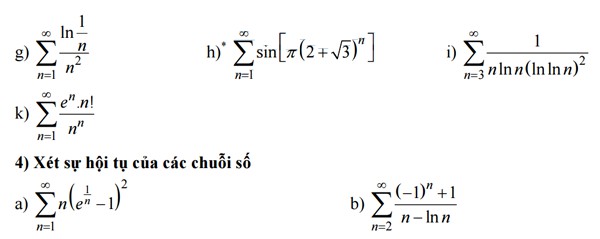
Ví dụ 5
Điều quan trọng cần lưu ý là, hiệu số chung không nhất thiết là một số dương, có thể có một hiệu số chung âm như được minh họa trong chuỗi số dưới đây:
25, 23, 21, 19, 17, 15 …….
Sự khác biệt phổ biến trong trường hợp này là -2. Công thức số học có thể được sử dụng để tìm bất kỳ số hạng nào trong chuỗi. Ví dụ, để có số hạng thứ 4 .
Số hạng thứ 4 = 25 + (4-1) – 2
= 25 – 6
= 19
Dãy hình học là một dãy số trong đó số sau hoặc số tiếp theo nhận được bằng cách nhân số trước với hằng số được gọi là tỷ số chung. Dãy số hình học được tổng quát trong công thức:
x n = x 1 × r n-1
Ở đâu;
x n = số hạng thứ n ,
x 1 = số hạng đầu tiên,
r = tỷ lệ chung, và
n = số điều khoản.
Ví dụ 6
Ví dụ, cho một dãy số như 2, 4, 8, 16, 32, 64, 128,…, số hạng thứ n có thể được tính bằng cách áp dụng công thức hình học.
Để tính số hạng thứ 7 , hãy xác định số hạng đầu tiên là 2, tỷ số chung là 2 và n = 7.
Số hạng thứ 7 = 2 x 2 7-1
= 2 x 2 6
= 2 x 64
= 128
Ví dụ 7
Một chuỗi hình học có thể bao gồm các số hạng giảm dần như trong ví dụ sau:
2187, 729, 243, 81,
Trong trường hợp này, tỷ lệ chung được tìm thấy bằng cách chia số hạng tiền nhiệm với số hạng tiếp theo. Chuỗi này có tỷ lệ chung là 3.
Đây là một dãy số mà số hạng đầu tiên đại diện cho các số hạng được liên kết với các dấu chấm được trình bày trong hình. Đối với một số hình tam giác, dấu chấm hiển thị số lượng dấu chấm cần thiết để điền vào một hình tam giác. Dãy số tam giác được cho bởi;
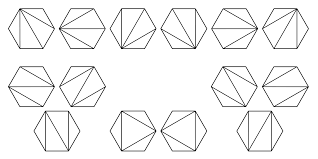

xn = (n 2 + n) / 2.
Ví dụ 8
Lấy ví dụ về chuỗi tam giác sau:
1, 3, 6, 10, 15, 21 ………….
Mẫu này được tạo ra từ các chấm lấp đầy một hình tam giác. Có thể lấy chuỗi bằng cách thêm các dấu chấm ở hàng khác và đếm tất cả các dấu chấm.
Một số bình phương là đơn giản hóa tích của một số nguyên với chính nó. Các số bình phương luôn dương, một dãy số bình phương được biểu diễn bằng công thức
x n = n 2
Ví dụ 9
Hãy nhìn vào chuỗi số bình phương; 4, 9, 16, 25, 36 ………. Dãy này lặp lại chính nó bằng cách bình phương các số nguyên sau: 2, 3, 4, 5, 6 …….
Dãy số lập phương là một dãy số được tạo ra bằng cách nhân một số với chính nó 3 lần. Công thức chung cho chuỗi số lập phương là:
x n = n 3
Chuỗi Fibonacci
Một chuỗi toán học bao gồm một mẫu trong đó số hạng tiếp theo thu được bằng cách thêm hai số hạng vào trước nó.
Ví dụ 10
Một ví dụ về chuỗi số Fibonacci là:
0, 1, 1, 2, 3, 5, 8, 13,…
Ví dụ, số hạng thứ ba của chuỗi này được tính là: 0 + 1 + 1 = 2, tương tự, số hạng thứ 7 được tính là 8 + 5 = 13.
Theo định nghĩa, một dãy số sinh đôi bao gồm sự kết hợp của hai dãy số. Các số hạng xen kẽ của chuỗi đôi có thể tạo ra một chuỗi độc lập khác.
Ví dụ về chuỗi đôi được đưa ra như: 3, 4, 8, 10.13, 16,… ..Khi kiểm tra kỹ chuỗi này, hai chuỗi được tạo ra là 1, 3, 8,13 và 2, 4, 10,16.
Xem thêm:
Các loại số trong toán học cho người chưa rõ
Cách tính căn bậc hai của một số nhanh gọn đơn giản nhất
Đây là một dãy số được hình thành bởi sự kết hợp của cả dãy số học và số học. Sự khác biệt của các số hạng liên tiếp trong loại chuỗi này tạo ra một chuỗi hình học. Lấy một ví dụ về dãy số học-đại số học này:
1, 2, 6, 36, 44, 440,…
Loại chuỗi này là một chuỗi được tạo ra mà không có quy tắc thích hợp.
Ví dụ 11
Ví dụ; 10, 22, 46, 94, 190,…., Có thể được giải quyết bằng cách sử dụng các bước sau:
10 x 2 = 20 + 2 = 22
22 x 2 = 44 + 2 = 46
46 x 2 = 92 + 2 = 94
190 x 2 = 380 + 2 = 382
Do đó, số hạng còn thiếu là 382.
Mẫu số nói chung là một chuỗi hoặc một mẫu trong một loạt các số hạng. Ví dụ: mẫu số trong chuỗi sau là +5:
0, 5, 10, 15, 20, 25, 30 ………
Để giải quyết các vấn đề về mẫu số, hãy kiểm tra chặt chẽ quy tắc chi phối mẫu.
Thử bằng các phép cộng, trừ, nhân hoặc chia giữa các số hạng liên tiếp.
Tóm lại, các vấn đề liên quan đến chuỗi số và mẫu đòi hỏi bạn phải kiểm tra mối quan hệ giữa những con số này. Bạn nên kiểm tra mối quan hệ số học như phép trừ và phép cộng. Kiểm tra mối quan hệ hình học bằng cách chia và nhân các số hạng để tìm tỉ số chung của chúng.
Câu hỏi thực hành