Công thức tính diện tích mặt cầu ngoại tiếp

Mặt cầu là giao hội các điểm M trong không gian cách điểm O nhất thiết một khoảng R gọi là tâm cầu O, bán kính R, kí hiệu: S(O; R) hay M/OM = R, vậy công thức tính diện tích mặt cầu ngoại tiếp là gì, mời các bạn hãy đọc bài viết do tintuctuyensinh liệt kê Công thức tính diện tích mặt cầu ngoại tiếp dưới đây nhe

CÔNG THỨC DIỆN TÍCH MẶT CẦU NGOẠI TIẾP

Công Thức Tính Diện Tích Mặt Cầu Ngoại Tiếp

SC = 4.Π.R²

Với: SC là kí hiệu diện tích mặt cầu
R là bán kính mặt cầu ngoại tiếp

– Trục đáy: Là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
– Trung trực của đoạn thẳng: Là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
– Mặt trung trực của đoạn thẳng: Mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.

Cách Tìm Tâm Và Bán Kính Mặt Cầu Của Các Hình căn bản

– Tâm và bán kính mặt cầu là hai đại lượng cần thiết để tính diện tích của mặt cầu ngoại tiếp, chính bởi thế xác định tâm và bán kính là thao tác quan trọng để các em có thể tìm được diện tích. Cùng theo dõi cách tìm tâm và cách tính bán kính của mặt cầu ngoại tiếp một số hình.

1. Hình lăng trụ đứng

Hình lăng trụ đứng A₁A₂A₃A₄.A’₁A’₂A’₃A’₄ có nhì đáy nội tiếp đường tròn O và O’.

– Tâm mặt cầu: I và I’ (đều là trung điểm của OO’)

– Bán kính mặt cầu ngoại tiếp: R = IA₁ = IA₂ = ….

– Biết tâm, bán kính, ứng dụng công thức tính diện tích mặt cầu ngoại tiếp, thay số và tính toán.

2. Hình chóp

a) Hình chóp đều

* Xác định tâm mặt cầu: Hình chóp đều SABC có:

– O là tâm của đáy => SO là trục đáy

– Trên mặt phẳng (SAO), vẽ d là đường trung trực của SA cắt SA tại giao điểm M, cắt SO tại giao điểm I

=> Tâm mặt cầu ngoại tiếp hình chóp chính là I.

* Tính bán kính mặt cầu ngoại tiếp:

Xét hai tam giác đồng dạng với nhau là SMI và SOA, ta có:

=> R = si mê = = SA² : 2.SO = IB = IB = IC

* Tìm diện tích mặt cầu ngoại tiếp:

=> Sau khi tính được bán kính mặt cầu, ta áp dụng công thức: SC = 4.Π.R²

b) Hình chóp có cạnh bên vuông góc với mặt phẳng đáy

* Tìm tâm mặt cầu: Hình chóp SABC có SA vuông góc với mặt đáy (ABC) trong đó mặt đáy ABC nội tiếp đường tròn tâm O
– Từ tâm O ngoại tiếp của đường tròn đáy, vẽ d vuông góc với (ABC) tại O.
– Trong mặt phẳng được tạo bởi đường thẳng d với SA, vẽ đường trung trực d’ của SA, giao với SA tại M, giao với d tại I.
* Tính bán kính mặt cầu ngoại tiếp:

Từ các dữ kiện đã biết, ta có hình chữ nhật MIOB

– Xét tam giác vuông MAI tại M:

R = AI = √(MI² + MA²) = √[AO² + (SA/2)²]

3. Hình hộp chữ nhật, hình lập phương

* Xác định tâm của mặt cầu:
– Tâm của mặt cầu chính là trung điểm của đoạn thẳng AC’ (tâm đối xứng của hình hộp chữ nhật/ hình lập phương).
* Tính bán kính mặt cầu ngoại tiếp: R =
– Bán kính mặt cầu = 1/2 độ dài đường chéo của hình hộp chữ nhật / hình lập phương.
* vận dụng công thức tính SC để tính diện tích.

5 mẫu Phân tích Chiếc thuyền ngoài xa

Phép đối xứng trục

Sự khác biệt giữa Danh sách và Tuple tron

Công Thức tác động tới Diện Tích Mặt Cầu Ngoại Tiếp Hình Chóp

Để tính được diện ích mặt cầu ngoại tiếp, Anh chị cần tính được bán kính ngoại tiếp. Anh chị cùng xem công thức tính bán kính mặt cầu ngoại tiếp để vận dụng vào trong bài cho đúng.

Bài Tập Tính Diện Tích Mặt Cầu Ngoại Tiếp

Bài tập 1: Cho hình chóp tam giác S.ABC, SAB là tam giác đều, đáy ABC là tam giác đều có cạnh bằng a, (SAB) vuông (ABC). Tính diện tích mặt cầu ngoại tiếp S.ABC.

Bài giải:

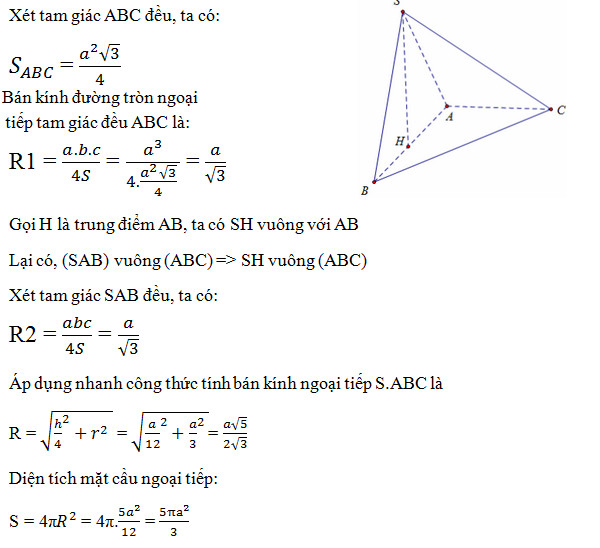
Bài tập 2: Cho hình chóp S.ABCD, đáy ABCD là hình vuông có cạnh bằng a, SA = a√3, SA ⊥ (ABCD). Tính diện tích mặt cầu ngoại tiếp hình chóp.

Công thức tính diện tích mặt cầu ngoại tiếp tương đối đơn giản, dễ nhớ, dễ thuộc, tuy nhiên trong từng dạng bài tập các em cần vận dụng một cách linh hoạt để tìm ra đáp án đúng mực nhất cho đề bài. Trong khi các em cũng cần hiểu và ghi nhớ cách tính diện tích hình tròn để dễ dãi ứng dụng những loại hình gần giống trong hình học không gian nhé.