Cặp phương trình tuyến tính trong hai biến
Contents
Đa giác là gì?
Đa giác là một hình khép kín được tạo thành từ các đoạn thẳng (không phải đường cong) trong một mặt phẳng hai chiều. Polygon là sự kết hợp của hai từ, tức là poly (có nghĩa là nhiều) và gon (có nghĩa là các cạnh).
Cần có tối thiểu ba đoạn thẳng để kết nối đầu cuối để tạo thành một hình khép kín. Vì vậy, một đa giác có tối thiểu ba cạnh được gọi là Tam giác và nó còn được gọi là 3-gon. Một đa giác n cạnh được gọi là n-gon.
Hình đa giác
Theo định nghĩa, chúng ta biết rằng đa giác được tạo thành từ các đoạn thẳng. Dưới đây là hình dạng của một số đa giác được bao bởi số lượng đoạn thẳng khác nhau.
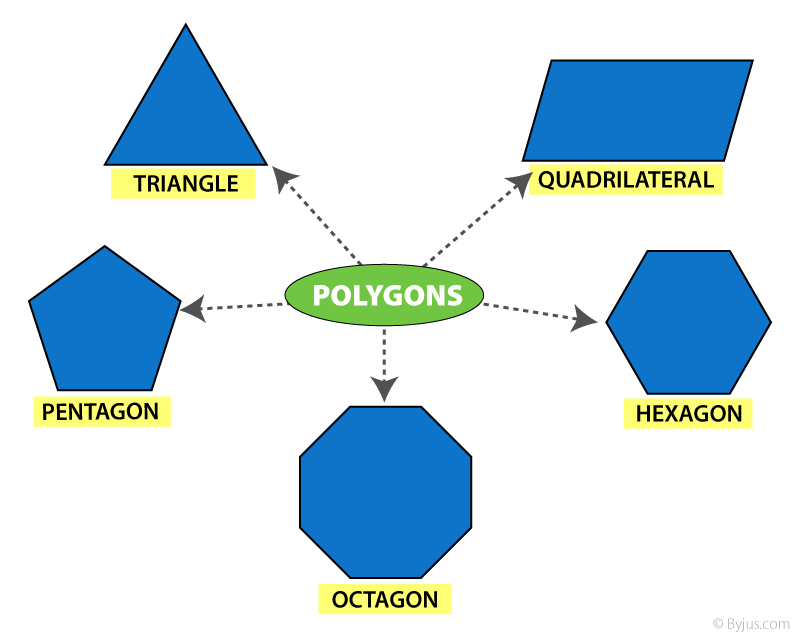

Các loại đa giác
Tùy thuộc vào các cạnh và góc, các đa giác được phân thành các loại khác nhau, cụ thể là:
- Đa giác đều
- Đa giác không đều
- Đa giác lồi
- Đa giác lõm
Đa giác đều
Nếu tất cả các cạnh và các góc trong của đa giác bằng nhau thì đa giác đó được gọi là đa giác đều. Các ví dụ về đa giác đều là hình vuông, hình thoi, tam giác đều, v.v.
Đa giác không đều
Nếu tất cả các cạnh và các góc bên trong của đa giác có số đo khác nhau, thì nó được gọi là đa giác không đều. Ví dụ, một tam giác vô hướng, một hình chữ nhật, một cánh diều, v.v.
Đa giác lồi
Nếu tất cả các góc bên trong của một đa giác đều nhỏ hơn 180 độ thì nó được gọi là đa giác lồi. Đỉnh sẽ hướng ra ngoài từ tâm của hình dạng.
Đa giác lõm
Nếu một hoặc nhiều góc bên trong của đa giác lớn hơn 180 độ, thì nó được gọi là đa giác lõm. Một đa giác lõm có thể có ít nhất bốn cạnh. Đỉnh hướng vào bên trong của đa giác.
Tuy nhiên, một số đa giác được xác định dựa trên số cạnh, góc và tính chất của chúng. Chúng ta hãy xem một trong những loại đa giác thường được sử dụng và chính là hình tam giác.
Góc của đa giác
Như chúng ta đã biết, bất kỳ đa giác nào cũng có bao nhiêu đỉnh thì nó cũng có các cạnh. Mỗi góc có một số đo các góc nhất định. Các góc này được phân loại thành hai loại là góc bên trong và góc bên ngoài của một đa giác .
Sở hữu góc nội thất
Tổng của tất cả các góc bên trong của một n-gon đơn giản = (n – 2) × 180 °
Hoặc là
Tổng = (n – 2) π radian
Trong đó ‘n’ bằng số cạnh của một đa giác.
Ví dụ, một tứ giác có bốn cạnh, do đó, tổng của tất cả các góc trong được cho bởi:
Tổng các góc trong của đa giác 4 cạnh = (4 – 2) × 180 °
= 2 × 180 °
= 360 °
Thuộc tính góc ngoại thất
Tổng các góc bên trong và bên ngoài tương ứng tại mỗi đỉnh của bất kỳ đa giác nào là bổ sung cho nhau. Đối với một đa giác;
|
Tính chất
Các tính chất của đa giác dựa trên các cạnh và góc của nó.
- Tổng tất cả các góc trong của một đa giác n mặt là (n – 2) × 180 °.
- Số đường chéo của một đa giác có n cạnh = n (n – 3) / 2
- Số tam giác được tạo thành bằng cách nối các đường chéo từ một góc của đa giác = n – 2
- Số đo mỗi góc trong của đa giác đều n mặt = [(n – 2) × 180 °] / n
- Số đo của mỗi góc bên ngoài của một đa giác đều n mặt = 360 ° / n
Công thức Diện tích và Chu vi
Diện tích và chu vi của các đa giác khác nhau dựa trên các cạnh.
Diện tích: Diện tích được định nghĩa là vùng được bao phủ bởi một đa giác trong một mặt phẳng hai chiều.
Chu vi: Chu vi của một đa giác là tổng khoảng cách được bao phủ bởi các cạnh của một đa giác.
Các công thức về diện tích và chu vi của các đa giác khác nhau được đưa ra dưới đây:
| Tên của đa giác | Khu vực | Chu vi |
| Tam giác | ½ x (cơ sở) x (chiều cao) | a + b + c |
| Quảng trường | mặt 2 | 4 (bên) |
| Hình chữ nhật | Chiều dài x Chiều rộng | 2 (chiều dài + chiều rộng) |
| Hình bình hành | Cơ sở x Chiều cao | 2 (Tổng các cặp cạnh liền kề) |
| Hình thang | Diện tích = 1/2 (tổng của cạnh song song) chiều cao | Tổng của tất cả các bên |
| Hình thoi | ½ (Sản phẩm của các đường chéo) | 4 x bên |
| Hình năm góc | 145 ( 5 + 25-√)———√s tôi de2 | Tổng của tất cả năm mặt |
| Hình lục giác | 3 √3 / 2 (cạnh) 2 | Tổng của tất cả sáu cạnh |
Hình tam giác (3-gon)
Tam giác là dạng đa giác đơn giản nhất có ba cạnh và ba đỉnh. Các hình tam giác cũng được phân thành nhiều loại khác nhau, dựa trên các cạnh và góc.
Một sự thật thú vị về Tam giác:
|
Hình tam giác – Dựa trên các mặt
- Tam giác đều – Có tất cả các cạnh bằng nhau và các góc có số đo bằng nhau. Nó còn được gọi là tam giác đồng dạng.
- Tam giác cân – Có 2 cạnh bất kỳ bằng nhau và các góc đối diện với các cạnh đó bằng nhau.
- Tam giác vô hướng – Có cả 3 cạnh không bằng nhau.
Xem hình bên dưới, để thấy sự khác biệt giữa ba loại hình tam giác.


Hình tam giác- Dựa trên góc
- Tam giác có góc nhọn – Mỗi góc nhỏ hơn 90 °
- Tam giác vuông góc – Một trong ba góc bất kỳ bằng 90 °
- Tam giác góc Obtuse – Bất kỳ một góc nào cũng lớn hơn 90 °
Hình dưới đây cho thấy ba loại góc, dựa trên các góc.


Một hoạt động:
|
Hình tứ giác (4 gon)
Tứ giác là một đa giác có số cạnh bằng bốn . Điều đó có nghĩa là, một đa giác được hình thành bằng cách bao quanh bốn đoạn thẳng sao cho chúng gặp nhau ở các góc / đỉnh để tạo thành 4 góc.
Giống như hình tam giác, hình tứ giác cũng được phân loại với nhiều loại khác nhau:
- Quảng trường
- Hình chữ nhật
- Hình bình hành
- Hình thoi
- Trapezium
Hình dưới đây cho thấy sự phân loại của các tứ giác.


Bảng dưới đây cho phép so sánh các cạnh đối diện, góc và đường chéo của các Tứ giác khác nhau.
| Tứ giác | Đối diện | Sides | Tất cả các bên bằng nhau | Các góc đối diện bằng | Đường chéo | Đường chéo |
| Song song, tương đông | Công bằng | Công bằng | Vuông góc | |||
| Hình chữ nhật | ✔ | ✔ | ✖ | ✔ | ✔ | ✔ |
| Hình bình hành | ✔ | ✔ | ✖ | ✔ | ✖ | ✖ |
| Hình thoi | ✔ | ✔ | ✔ | ✔ | ✖ | ✔ |
| Trapezium | ✖
(Chỉ một mặt) |
✖ | ✖ | ✖ | ✖ | ✖ |
| Quảng trường | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
Tên của Đa giác
| Đa giác | Số mặt | Số đường chéo | Số đỉnh | Góc nội thất |
| Tam giác | 3 | 0 | 3 | 60 |
| Tứ giác | 4 | 2 | 4 | 90 |
| Hình năm góc | 5 | 5 | 5 | 108 |
| Hình lục giác | 6 | 9 | 6 | 120 |
| Thất giác | 7 | 14 | 7 | 128.571 |
| Hình bát giác | số 8 | 20 | số 8 | 135 |
| Nonagon | 9 | 27 | 9 | 140 |
| Hình lục giác | 10 | 35 | 10 | 144 |
| Hendecagon | 11 | 44 | 11 | 147.273 |
| Dodecagon | 12 | 54 | 12 | 150 |
| Triskaidecagon | 13 | 65 | 13 | 158,308 |
| Tetrakaidecagon | 14 | 77 | 14 | 154.286 |
| Lầu Năm Góc | 15 | 90 | 15 | 156 |
Hình dạng ba chiều (hình dạng 3-D)
Hình dạng ba chiều là một vật thể rắn được tạo thành bởi sự kết hợp của các hình đa giác và hình 2d. Một số hình dạng 3D mà chúng ta có thể quan sát trong đời thực là:


- Đây là những hình dạng có thể được chiếu trên một mảnh giấy nhưng không thể được vẽ trên giấy. Những hình dạng này được gọi là chất rắn.
| Hình dạng 2-D (Đa giác) | Hình dạng 3-D |
| Cạnh | Cạnh |
| Dọc | Dọc |
| – | Khuôn mặt |
- Hình dạng 3-D có các khuôn mặt là đặc điểm phân biệt.


Câu hỏi thường gặp – Câu hỏi thường gặp
Đa giác là gì?
Thế nào được gọi là đa giác có 7 cạnh?
Thế nào được gọi là đa giác có 9 cạnh?
Một đa giác có bao nhiêu đường chéo?
Các loại đa giác khác nhau là gì?
Đa giác đều – tất cả các cạnh và số đo các góc bên trong đều bằng nhau
Đa giác không đều – tất cả các cạnh và số đo các góc trong không bằng nhau, tức là các
đa giác Lồi khác nhau – tất cả các góc trong của một đa giác đều nhỏ hơn 180 độ. Đỉnh sẽ hướng ra ngoài từ tâm của hình
Đa giác lõm – một hoặc nhiều góc bên trong của đa giác lớn hơn 180 độ. Một đa giác lõm có thể có ít nhất bốn cạnh. Đỉnh hướng vào bên trong của đa giác.