Định lý nhị thức dễ hiểu ai cũng học được

Định lý nhị thức – Giải thích & Ví dụ

Đa thức là một biểu thức đại số được tạo thành từ hai hoặc nhiều số hạng bị trừ, cộng hoặc nhân. Một đa thức có thể chứa các hệ số, biến, số mũ, hằng số và các toán tử như phép cộng và phép trừ. Có ba loại đa thức, đó là đơn thức tử, đơn thức nhị thức và đơn thức bậc ba.

Đơn thức là một biểu thức đại số chỉ có một số hạng, trong khi một đơn thức là một biểu thức chứa đúng ba số hạng.

Định lý nhị thức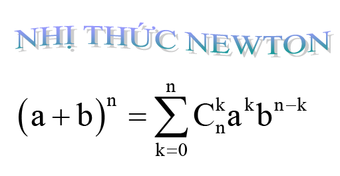

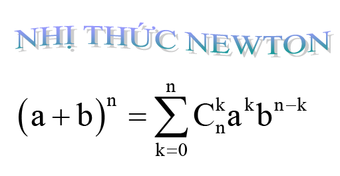
Biểu thức nhị thức là gì?

Trong Đại số, một biểu thức nhị thức là một biểu thức chứa hai số hạng được nối với nhau bằng dấu cộng hoặc dấu trừ. Ví dụ, (x + y) và (2 – x) là các ví dụ về biểu thức nhị thức.

Đôi khi, chúng ta có thể cần mở rộng các biểu thức nhị thức như hình dưới đây.

( a  +  b ) ⁰  = 1

( a  +  b ) ¹  =  a  +  b

( a  +  b ) ²  =  a ²  + 2 ab  +  b ²

( a  +  b ) ³  =  a ³  + 3 a ² b  + 3 ab ²  +  b ³

( a  +  b ) ⁴  =  a ⁴  + 4 a ³ b  + 6 a ² b ²  + 4 ab ³  +  b ⁴

( a  +  b ) ⁵  =  a ⁵  + 5 a ⁴ b  + 10 a ³ b ²  + 10 a ² b ³  + 5 ab ⁴  +  b ⁵

Bạn nhận ra rằng việc mở rộng một biểu thức nhị thức bằng phép nhân trực tiếp như được hiển thị ở trên là khá phức tạp và không thể áp dụng cho số mũ lớn hơn.

Trong bài này, chúng ta sẽ học cách sử dụng định lý Nhị thức để khai triển biểu thức nhị thức mà không cần phải nhân mọi thứ một cách dài dòng.

Định lý Nhị thức là gì?

Dấu vết của định lý nhị thức đã được con người biết đến từ thế kỷ ^thứ 4 trước Công nguyên. Nhị thức cho hình khối được sử dụng vào thế kỷ ^thứ 6 sau Công nguyên. Một nhà toán học Ấn Độ, Halayudha, giải thích phương pháp này sử dụng tam giác Pascal trong 10 ^thứ thế kỷ.

Những tuyên bố rõ ràng về định lý này đã được ghi trong 12 ^thứ thế kỷ. Các nhà toán học đưa những phát hiện này sang các giai đoạn tiếp theo cho đến khi Ngài Isaac Newton tổng quát hóa định lý nhị thức cho tất cả các số mũ vào năm 1665.

Định lý Nhị thức phát biểu khai triển đại số các số mũ của một nhị thức, có nghĩa là có thể khai triển một đa thức (a + b) ⁿ thành nhiều số hạng.

Về mặt toán học, định lý này được phát biểu là:

(a + b) ⁿ = a ⁿ + ( ⁿ ₁ ) a ^{n – 1} b ¹ + ( ⁿ ₂ ) a ^{n – 2} b ² + ( ⁿ ₃ ) a ^{n – 3} b ³ + ……… + b ⁿ

trong đó ( ⁿ ₁ ), ( ⁿ ₂ ),… là các hệ số của nhị thức.

Dựa vào các tính chất trên của Định lý Nhị thức, ta có thể suy ra Công thức Nhị thức là:

(a + b) ⁿ = a ⁿ + na ^{n – 1} b ¹ + [n (n – 1) / 2!] a ^{n – 2} b ² + [n (n – 1) (n – 2) / 3! ] a ^{n – 3} b ³ + ……… + b ⁿ

Ngoài ra, chúng ta có thể biểu diễn công thức Nhị thức như sau:

(a + b) ⁿ = ⁿ C ₀ a ⁿ + ⁿ C ₁ a ^{n – 1} b + ⁿ C ₂ a ^{n – 2} b ² + ⁿ C ₃ a ^{n – 3} b ³ + ………. + ⁿ C _n b ⁿ

Trong đó ( ⁿ _r ) = ⁿ C _r = n! / {r! (n – r)!} và (C) và (!) lần lượt là tổ hợp và giai thừa.

Ví dụ:

• 3! = (3) (2) (1) = 6
• 5! = (5) (4) (3) (2) (1) = 120
• 4! / 2! = (4) (3) (2) (1) / (2) (1) = 12
• ¹⁰C ₆  = 10! / (10 – 6)! 6! = 10! / 4! 6! = (1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10) / 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 x 5 x 6 = 7 x 8 x 9 x 10 / 1 x 2 x 3 x 4 = 7 x 3 x 10 = 210.

Xem thêm

Cách cộng và Trừ đa thức như thế nào? Chi tiết cách thực hiện

Hướng dẫn định lý nhân tố đơn giản, dễ hiểu nhất

Cách sử dụng Định lý nhị thức?

Có một số điều bạn cần nhớ khi áp dụng Định lý nhị thức.

Đó là:

• Số mũ của số hạng đầu tiên (a) giảm từ n xuống 0
• Số mũ của số hạng thứ hai (b) tăng từ 0 đến n
• Tổng các số mũ của a và b bằng n.
• Hệ số của số hạng đầu tiên và số hạng cuối cùng bằng 1.

Hãy sử dụng Định lý nhị thức trên các biểu thức nhất định để hiểu định lý một cách thực tế.

ví dụ 1

Mở rộng (a + b) ⁵

Giải pháp

⟹ (a + b) ⁵ = a ⁿ + ( ⁵ ₁ ) a ^{5– 1} b ¹ + ( ⁵ ₂ ) a ^{5 – 2} b ² + ( ⁵ ₃ ) a ^{5– 3} b ³ + ( ⁵ ₄ ) a ^{5 – 4} b ⁴ + b ⁵

= a ⁵  + 5 a ⁴ b  + 10 a ³ b ²  + 10 a ² b ³  + 5 ab ⁴  +  b ⁵

Ví dụ 2

Khai triển ( x  + 2) ⁶ bằng cách sử dụng Định lý nhị thức.

Giải pháp

Cho a = x;

b = 2 và n = 6

Thay thế các giá trị trong công thức nhị thức

(a + b) ⁿ = a ⁿ + na ^{n – 1} b ¹ + [n (n – 1) / 2!] a ^{n – 2} b ² + [n (n – 1) (n – 2) / 3! ] a ^{n – 3} b ³ + ……… + b ⁿ

⟹ (x + 2) ⁶ = x ⁶ + 6x ⁵ (2) ¹ + [(6) (5) / 2!] (X ⁴ ) (2 ² ) + [(6) (5) (4) / 3 !] (x ³ ) (2 ³ ) + [(6) (5) (4) (3) / 4!] (x ² ) (2 ⁴ ) + [(6) (5) (4) (3) (2) / 5!] (X) (2 ⁵ ) + (2) ⁶

= x ⁶ + 12x ⁵ + 60x ⁴ + 160x ³ + 240x ² + 192x + 64

Ví dụ 3

Sử dụng định lý nhị thức để khai triển (2 x  + 3) ⁴

Giải pháp

Bằng cách so sánh với công thức nhị thức, chúng tôi nhận được,

a = 2x, b = 3 và n = 4.

Thay thế các giá trị trong công thức nhị thức.

⟹ (2x + 3) ⁴ = x ⁴ + 4 (2x) ³ (3) + [(4) (3) / 2!] (2x) ² (3) ² + [(4) (3) (2) / 4!] (2x) (3) ³ + (3) ⁴

= 16 x ⁴ + 96x ³ + 216x ² + 216x + 81

Ví dụ 4

Tìm khai triển của (2x – y) ⁴

Giải pháp

(2x – y) ⁴ = (2x) + (−y) ⁴ = (2x) ⁴ + 4 (2x) ³ (−y) + 6 (2x) ² (−y) ² + 4 (2x) (−y ) ³ + (−y) ⁴

= 16x ⁴ – 32x ³ y + 24x ² y ² – 8xy ³ + y ⁴

Ví dụ 5

Sử dụng Định lý nhị thức để khai triển (2 + 3x) ³

Giải pháp

Bằng cách so sánh với công thức Nhị thức,

a = 2; b = 3x và n = 3

⟹ (2 + 3x) ³ = 2 ³ + ( ³ ₁ ) 2 ² (3x) ¹ + ( ³ ₂ ) 2 (3x) ² + (3x) ³

= 8 + 36x + 54x ² + 27x ³

Ví dụ 6

Mở rộng (x ²  + 2) ⁶

Lời giải
(x ²  +2) ⁶  =  ⁶ C ₀  (x ² ) ⁶ (2) ⁰  +  ⁶ C ₁ (x ² ) ⁵ (2) ¹  +  ⁶ C ₂ (x ² ) ⁴ (2) ²  +  ⁶ C ₃  (x ² ) ³ (2) ³  +  ⁶ C ₄  (x ² ) ² (2) ⁴  +  ⁶ C₅  (x ² ) ¹ (2) ⁵  +  ⁶ C ₆  (x ² ) ⁰ (2) ⁶

= (1) (x ¹² ) (1) + (6) (x ¹⁰ ) (2) + (15) (x ⁸ ) (4) + (20) (x ⁶ ) (8) + (15) (x ⁴ ) (16) + (6) (x ² ) (32) + (1) (1) (64)

= x ¹²  + 12 x ¹⁰  + 60 x ⁸  + 160 x ⁶  + 240 x ⁴  + 192 x ²  + 64

Ví dụ 7

Khai triển biểu thức (√2 + 1) ⁵  + (√2 – 1) ⁵ bằng công thức Nhị thức.

Giải pháp

(x + y) ⁵  + (x – y) ⁵  = 2 [5C ₀  x ⁵  + 5C ₂  x ³  y ²  + 5C ₄  xy ⁴ ]

= 2 (x ⁵  + 10 x ³  y ²  + 5xy ⁴ )

= (√2 + 1) ⁵  + (√2 – 1) ⁵  = 2 [(√2) ⁵  + 10 (√2) ³ (1) ²  + 5 (√2) (1) ⁴ ]

= 58√2