Định lý pitago là gì? Cách sử dụng định lý pitago

KHOA Y DƯỢC HÀ NỘI

Thẳng tiến vào đại học chỉ với: Điểm lớp 12 Từ 6,5 – Điểm thi từ 18 năm 2022

Bạn đang tìm hiểu những thông tin liên quan đến định lý Pitago và các công thức liên quan đến công thức này. Những câu hỏi đặt ra định lý Pitago là gì và cách giải quyết các bài toán liên quan đến định lý Pytago là gì?

Để giải đáp những thắc mắc trên hôm nay tintuctuyensinh của chúng tôi sẽ giúp bạn hệ thống lại phần lý thuyết liên quan đến định lý Pytago cũng như các ví dụ và các dạng bài tập áp dụng liên quan đến định lý Pitago. Trên cơ sở đó giúp các bạn tổng hợp và hệ thống lại các kiến thức mà mình được học trong chương trình môn Toán học nói chung.

1, NHẬN THỨC CHUNG ĐỊNH LÝ PITAGO

Như các bạn đã biết trong chương trình môn Toán học lớp 7 chúng ta đã được tiếp xúc với khái niệm định lý Pitago vậy câu hỏi đặt ra định lý Pitago là gì và được ứng dụng như thế nào.

Định lý Pytago là gì?

Định lý Pitago được đánh giá là một công thức nền tảng mở đầu cho phần hình học và đây là kiến thức trọng tâm dùng để giải quyết các bài tập liên quan đến chứng minh, tính toán sau này.

Nội dung định lý Pitago được phát biểu như sau:

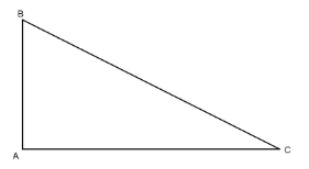
Trong một tam giác vuông bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Đây là Khái niệm định lí Pytago mà bạn thường gặp gặp ngoài ra còn có định lý Pitago đảo có nội dung như sau:

Nếu trong một tam giác bất kỳ có bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại thì tam giác đã cho là tam giác vuông.

2, VÍ DỤ MINH HỌA CÁCH SỬ DỤNG ĐỊNH LÝ PITAGO

Ví dụ 1: Nếu nếu độ dài hai cạnh bên của một tam giác vuông tăng lên lần lượt 2, 3 lần thì độ dài của cạnh huyền của tam giác vuông đã thay đổi như thế nào?

Hướng dẫn giải:

Ta gọi Gọi b, c lần lượt là độ dài của hai cạnh bên của tam giác vuông

a là độ dài cạnh huyền của tam giác vuông khi đó áp dụng định lý Pitago ta có công thức:

a2 = b2 + c2 (1)

Mà theo đề bài ta có độ dài hai cạnh bên của tam giác vuông tăng lên lần lượt là 2 lần khi đó ta có b’ = 2b và c’ = 2c

Thay vào công thức a’2 = b’2 + c’2 = (2b)2 + (2c)2 = 4 (b2 + c2) = 4a2

Tương đương a’2 = 4a2 hay a’ = 2a

Vậy kết luận khi tăng độ dài các cạnh bên của tam giác vuông lên 2 lần thì độ dài cạnh huyền cũng tăng lên 2 lần.

Tương tự khi tăng độ dài các cạnh bên của tam giác vuông lên 3 lần thì độ dài cạnh huyền cũng tăng lên 3 lần.

Ví dụ 2: Cho tam giác vuông ABC vuông tại A Gọi M là trung điểm của AB. Kẻ MH vuông góc với BC tại H hát chứng minh CH2 – BH2 = AC2

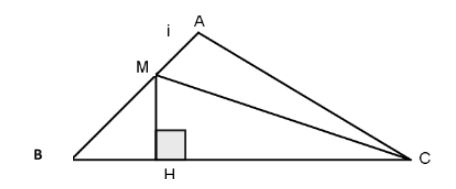
Hướng dẫn giải:

Từ các dữ kiện của bài toán ta có hình vẽ như sau:

Nối C với M ta được tam giác vuông CHM

Áp dụng định lý Pytago trong tam giác CHM ta có CH2 = MC2 – MH2

khi đó CH2 – BH2 = MC2 – MH2 – BH2 = MC2 – (MH2 + BH2) = MC2 – BM2

Mà MA = MB do M là trung điểm của AB

Do đó CH2 – BH2 = MC2 – AM2 = AC2

Suy ra điều phải chứng minh.

Ví dụ 3: Cho tam giác thường ABC có AH vuông góc với BC trong đó H thuộc cạnh BC. Tính chu vi của tam giác ABC biết AC = 10 cm AH = 8 cm BH = 4 cm.

Hướng dẫn giải:

Theo điều kiện bài toán ta có hình vẽ như sau:

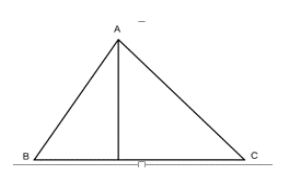
Trong tam giác ABH vuông tại H

áp dụng định lý Pitago ta có AB2 = AH2 + HB2 = 82 + 42 = 80 => AC = 80 cm

Tương tự trong tam giác ACH vuông tại H

áp dụng định lý Pitago ta có HC2 = AC2 – AH2 = 102 – 82 = 36 => HC = 6 cm

BC = BH + HC = 4 + 6 = 10 cm

Vậy chu vi của tam giác ABC bằng:

AB + BC + AC = 80 + 10 + 10 (cm)

Như vậy qua các ví dụ trên đây đã giúp bạn nắm được những phần kiến thức cơ bản liên quan đến định lý Pitago cũng như cung cấp những kiến thức nền tảng quan trọng để bạn giải quyết các bài tập khó hơn liên quan đến định lý Pitago.

Trên đây là toàn bộ những kiến thức và các ví dụ minh họa liên quan đến định lý Pitago mà tintuctuyensinh của chúng tôi đã cung cấp cho các bạn tham khảo. Hy Vọng đây là nguồn tài liệu bổ ích cho các bạn nghiên cứu học tập, từ đó lựa chọn và hệ thống lại cho mình các kiến thức quan trọng để có thể tìm ra phương pháp học tập hiệu quả và hoàn thành tốt các bài tập mà mình gặp phải.

Xem thêm: