Chi tiết cách tìm một đơn vị Vector chỉ trong giây lát

Cũng giống như trong Vật lý, mọi đại lượng đo được đều có đơn vị đo. Tương tự, trong hình học vectơ, mọi vectơ cũng có một đơn vị đo, có thể được gọi là Vectơ đơn vị. Nói cách đơn giản hơn, một vectơ đơn vị có thể được định nghĩa là:

“Bất kỳ vectơ nào có độ lớn 1 đều có thể được mô tả là một Vectơ đơn vị.” 

Trong chủ đề vectơ đơn vị, chúng tôi sẽ đề cập đến các chủ đề sau:

• Vector đơn vị là gì?
• Làm thế nào để tìm một Vector đơn vị?
• Làm thế nào để tìm một Vectơ đơn vị cùng hướng?
• Công thức cho Vectơ đơn vị là gì?
• Các tính chất của một Vectơ đơn vị là gì?
• Các ví dụ
• Thực hành các vấn đề

Vectơ đơn vị là gì? 

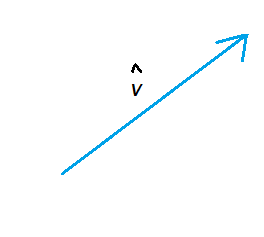
Vectơ đơn vị là một vectơ có độ lớn là 1, hay theo thuật ngữ toán học là một đơn vị. Trong hình học vectơ, ký hiệu của một vectơ đơn vị hơi khác một chút. Các vectơ đơn vị được biểu thị bằng cách đặt một mũ (^) trên đầu các vectơ. Vectơ v trong hình dưới đây là một vectơ đơn vị và có thể được biểu diễn bằng v ^.

Trong toán học và vật lý, chúng ta thường bắt gặp từ ‘đơn vị’. Nhưng chính xác nó có nghĩa là gì? Nếu chúng ta đi sâu vào toán học sơ cấp cơ bản, thì từ ‘đơn vị’ đã được định nghĩa ngay từ đầu của toán học. Đơn vị từ tượng trưng cho ‘1 ‘ . Đơn vị từ ‘; lần đầu tiên được tìm thấy trong hệ thống Giá trị Địa điểm toán học . Nền tảng của hệ thống dựa trên các đơn vị vì nó tượng trưng cho vị trí của ‘cái’.

Tương tự, trong lĩnh vực hình học vectơ, vectơ đơn vị cũng là viết tắt của ‘1’. Cần có một vectơ đơn vị để chia tỷ lệ một vectơ. Trong ngôn ngữ vật lý, chúng ta có thể mô tả tỷ lệ này là đo lường.

Các vectơ đơn vị về cơ bản là đơn vị của một vectơ và bất kỳ vectơ nào cũng có thể được biểu diễn dưới dạng vectơ đơn vị.

Vì vectơ đơn vị có độ lớn là 1, thông tin duy nhất mà chúng cung cấp liên quan đến vectơ là hướng của nó. Đây là lý do tại sao vectơ đơn vị còn được gọi là ‘Vectơ hướng’. Khi các vectơ đơn vị được sử dụng để chia tỷ lệ một vectơ, chúng cung cấp cho chúng ta hướng của vectơ cụ thể đó.

Ví dụ, vectơ v được hiển thị bên dưới có độ lớn là 3, nhưng vectơ này cũng có thể được biểu diễn theo vectơ đơn vị a , có độ lớn là 1, nhưng hướng của nó là đông bắc.

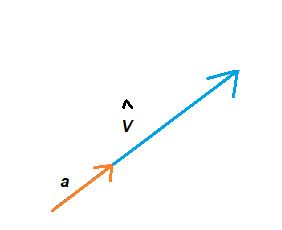
Vectơ đơn vị được sử dụng để chia tỷ lệ vectơ trong cả hai và ba chiều

Hướng của Vectơ Đơn vị 

Vectơ đơn vị của bất kỳ vectơ v nhất định tồn tại cùng hướng với vectơ v . Điều này là do vectơ đơn vị của bất kỳ vectơ nào đóng vai trò là đơn vị đo cho vectơ. Vì độ lớn của vectơ đơn vị đã là 1, nên nó chỉ tính theo hướng của vectơ v.

Đây là lý do tại sao vectơ đơn vị của bất kỳ vectơ v nào tồn tại cùng hướng với vectơ v. Cũng như các thành phần vectơ không phải là vectơ thực tồn tại ở một nơi. Tương tự, một vector đơn vị không tồn tại vật lý trong mặt phẳng. Mục đích duy nhất của nó là cung cấp một đơn vị đo cho bất kỳ vectơ nào và cung cấp cho vectơ một hướng cụ thể.

Cho dù một vectơ tồn tại trong mặt phẳng hai chiều hay ba chiều thì vectơ đó phải có vectơ đơn vị tương ứng của nó. Công thức tương tự cũng được áp dụng để tìm vectơ đơn vị trong cả hai chiều và ba chiều.

Hướng của các vectơ đơn vị trong hai chiều

Trong trường hợp mặt phẳng hai chiều, một thành phần, véc tơ đơn vị, hướng dọc theo trục x trong khi thành phần kia hướng dọc theo trục y.

Chúng tôi nhận thức rõ rằng chỉ có hai trục, x và y, tồn tại trong hai chiều. Các vectơ đơn vị trong hai chiều tồn tại như sau:

Hãy xem xét một vectơ v , có độ lớn 3, theo hai chiều như trong hình (1.2). Vectơ v này cũng có thể được mô tả dưới dạng các vectơ đơn vị, với các vectơ đơn vị đóng vai trò là thành phần của vectơ v . Vectơ này cũng có thể được viết dưới dạng các thành phần vectơ đơn vị của nó như sau:

v = 2x ^ + 2,25y ^

Xem thêm:

Cách tìm độ lớn vectơ đơn giản nhất cho bạn

Góc giữa hai Vectơ – Giải thích và Ví dụ

Hướng của các vectơ đơn vị trong ba chiều

Trong không gian ba chiều, một trục bổ sung được bao gồm, được gọi là trục z.

Các vectơ đơn vị trong ba chiều có thể được mô tả như sau:

v = x ^ + y ^ + z ^

ví dụ 1

Xác định xem một trong 2 vectơ là vectơ đơn vị

(i) v   = 0,5x (^) + 0,86y (^) (ii) v = 2x ^ + 3y ^

Giải pháp

Để tìm các vectơ đơn vị, chúng ta sẽ tìm độ lớn của cả hai vectơ này:

Đầu tiên hãy giải phương trình (i):

v = 0,5x ^ + 0,86y ^

| v | = √ ((0,5) ^ 2 + (0,86) ^ 2)

| v | = 0,99

| v | ≅ 1

Vậy vectơ (i) là một vectơ đơn vị.

Hãy xem phương trình (ii):

v = 2x ^ + 3y ^

| v | = √ ((2) ^ 2 + (3) ^ 2)

| v | = 3,6

Vậy vectơ (ii) không phải là vectơ đơn vị.

Làm thế nào để Tìm một véc tơ đơn vị?

Vì vectơ đơn vị chỉ được biết để xác định hướng của bất kỳ vectơ v nào, vectơ đơn vị của vectơ bất kỳ v có cùng hướng với vectơ v. Sau khi thực hiện các phép tính độ lớn cần thiết trên vectơ đơn vị đã xác định, và có thể thấy rõ rằng độ lớn dường như là 1. 

Chúng ta đã thảo luận rằng bất kỳ vectơ nào cũng có thể được biểu diễn theo các vectơ đơn vị của nó. Tương tự, chúng ta có thể tìm một vectơ đơn vị của bất kỳ vectơ đã cho nào có cùng hướng với vectơ đã cho.

Các ví dụ có thể củng cố khái niệm này.

Vì vậy, nói một cách đơn giản hơn, chúng ta có thể kết luận rằng mọi vectơ trong mặt phẳng hai chiều hoặc ba chiều đều bị ràng buộc đi kèm với vectơ đơn vị của nó chịu trách nhiệm mô tả hướng của vectơ.

Vectơ có thể tồn tại trong cả mặt phẳng hai chiều và ba chiều. Tương tự, các vectơ đơn vị của chúng cũng có thể tồn tại trong các mặt phẳng này. Mỗi vectơ đơn vị tồn tại dọc theo một trục cụ thể, cho dù là x, y hoặc z và vuông góc với các trục còn lại.

Công thức Tìm Vectơ Đơn vị

Đối với vectơ v bất kỳ, đơn vị đo tương ứng của nó, là vectơ đơn vị, tồn tại theo phương song song với vectơ v và có độ lớn bằng 1. Có thể tìm vectơ đơn vị này bằng cách áp dụng công thức sau:

Đơn vị vector = độ lớn của vector / vector

u = v / | v |

Vectơ đơn vị cũng có thể được ký hiệu là u.

Chúng ta có thể tóm tắt việc tìm vectơ đơn vị thành 4 bước cơ bản:

1. Lưu ý vectơ v với các thành phần đã cho dọc theo mỗi trục.
2. Tìm độ lớn của vectơ v.
3. Chia hai tham số.
4. Kiểm tra độ lớn của vectơ đơn vị thu được để chứng minh.

Công thức này bao gồm hai tham số, cả hai đều dựa trên vectơ v . Trong tử số, công thức cho thấy vectơ v tồn tại trong một mặt phẳng hai chiều hoặc ba chiều. Mẫu số cho biết độ lớn của vectơ v . Khi chia hai tham số, ta được vectơ đơn vị u của vectơ v .

Công thức này có thể được mở rộng cho cả bài toán hai chiều và ba chiều.

Tìm vectơ đơn vị trong hai chiều

Trong mặt phẳng hai chiều, vectơ v sẽ được biểu diễn bởi hai trục vuông góc với nhau, đó là trục x và trục y. Trong các ký hiệu toán học, vectơ đơn vị dọc theo trục x được biểu thị bằng i ^ và vectơ đơn vị dọc theo trục y được biểu diễn bằng j ^.

Vectơ v sau đó có thể được viết dưới dạng:

v = xi ^ + yj ^

Để viết các vectơ đơn vị này ở dạng phẳng, chúng ta có thể sử dụng các dấu ngoặc đơn như sau:

v = (x, y)

Do đó, chúng ta có thể viết lại công thức tìm vectơ đơn vị theo hai cách:

u = v / | v |

u = v / √ ((x) ^ 2 + (y) ^ 2)

Hoặc chúng ta cũng có thể viết nó là:

u = (x, y) / √ ((x) ^ 2 + (y) ^ 2)

Ví dụ 2

Tìm vectơ đơn vị của vectơ v đã cho là v = (3, 7)

Giải pháp

Chúng ta đã làm quen với công thức tìm véc tơ đơn vị:

u = v / | v |

Vì vậy, bằng cách đặt độ lớn:

u = (3, 7) / √ ((3) ^ 2 + (7) ^ 2)

u = (3, 7) / √ (58)

u = (3 / √58, 7 / √58)

Trong đó vectơ u là vectơ đơn vị.

Bằng chứng

Để chứng minh cho ví dụ đã cho, chúng ta sẽ tìm độ lớn của u:

u = (3 / √58, / √58)

| u | = √ ((3 / √58) ^ 2 + (7 / √58) ^ 2)

| u | = √1

| u | = 1

Đây là bằng chứng rằng vectơ u đã cho là một vectơ đơn vị của v. 

Ví dụ 3

Cho vectơ v = (-2, 3), hãy tìm vectơ đơn vị của nó.

Giải pháp

Công thức tìm vectơ đơn vị được phát biểu là:

u = v / | v |

Vì vậy, bằng cách chèn độ lớn của vectơ v :

u = (-2, 3) / √ ((- 2) ^ 2 + (3) ^ 2)

u = (-2, 3) / √13

u = (-2 / √13, 3 / √13)

Trong đó u là véc tơ đơn vị.

Bằng chứng

Để chứng minh cho ví dụ đã cho, chúng ta sẽ tìm độ lớn của u:

u = (-2 / √13, 3 / √13)

| u | = √ ((- 2 / √13) ^ 2 + (3 / √13) ^ 2)

| u | = √0,99

| u | = 1

Đây là bằng chứng rằng vectơ u đã cho là một vectơ đơn vị của v. 

Tìm vectơ đơn vị trong ba thứ nguyên

Trong mặt phẳng ba chiều, vectơ v sẽ được biểu diễn bởi ba trục vuông góc, đó là trục x, y và trục z. Trong các ký hiệu toán học, véc tơ đơn vị dọc theo trục x được biểu diễn bằng i ^. Vectơ đơn vị dọc theo trục y được biểu diễn bằng j ^ và vectơ đơn vị dọc theo trục z được biểu diễn bằng k ^.

Do đó vectơ v có thể được viết là:

v = xi ^ + yj ^ + zk ^

Để viết các vectơ đơn vị này ở dạng phẳng, chúng ta có thể sử dụng các dấu ngoặc đơn như sau:

v = (x, y, z)

Do đó, chúng ta có thể viết lại công thức tìm vectơ đơn vị theo hai cách:

u = v / | v |

u = v / √ ((x) ^ 2 + (y) ^ 2 + (z) ^ 2)

Hoặc chúng ta cũng có thể viết nó là:

u = (x, y, z) / √ ((x) ^ 2 + (y) ^ 2 + (z) ^ 2)

Ví dụ 4

Đối với vectơ v = (12, 3, -4), hãy tìm vectơ đơn vị của nó.

Giải pháp

Chúng ta đã làm quen với công thức tìm véc tơ đơn vị:

u = v / | v |

Vì vậy, bằng cách chèn các tham số cần thiết:

u = (12, 3, -4) / √ ((12) ^ 2 + (3) ^ 2 + (-4) ^ 2)

u = (12, 3, -4) / √169

u = (12, 3, -4) / 13

u = (13/12, 3/13, -4/13)

Vậy u là véc tơ đơn vị bắt buộc.

Bằng chứng

Để chứng minh, hãy tìm độ lớn của u:

u = (13/12, 3/13, -4/13)

| u | = √ ((13/12) ^ 2 + (3/13) ^ 2 + (-4/13) ^ 2)

| u | = √ (0,846 + 0,054 + 0,094)

| u | = √0,994

| u | = 1

Do đó, người ta chứng minh rằng vectơ u là vectơ đơn vị của v.

Ví dụ 5

Tìm vectơ đơn vị của vectơ v = (2, 4, 1).

Giải pháp

Công thức tìm vectơ đơn vị được phát biểu là:

u = v / | v |

Vì vậy, bằng cách chèn các tham số cần thiết:

u = (2, 4, 1) / √ ((2) ^ 2 + (4) ^ 2 + (1) ^ 2)

u = (2, 4, 1) / √21

u = (2 / √21, 4 / √21, 1 / √21)

Vậy u là véc tơ đơn vị bắt buộc.

Bằng chứng

Để chứng minh, hãy tìm độ lớn của u:

u = (2 / √21, 4 / √21, 1 / √21)

| u | = √ ((2 / √21) ^ 2 + (4 / √21) ^ 2 + (1 / √21) ^ 2)

| u | = √0,99

| u | = 1

Do đó, người ta chứng minh rằng vectơ u là vectơ đơn vị của v.

Các Thuộc Tính Của Một Vectơ Đơn Vị

Nội dung của chủ đề này có thể được tóm tắt trong các tính chất của một vectơ đơn vị theo cách sau:

1. Một vectơ đơn vị có độ lớn là 1.
2. Các vectơ đơn vị chỉ được sử dụng để xác định hướng của một vectơ.
3. Vectơ đơn vị tồn tại trong cả hai mặt phẳng hai chiều và ba chiều.
4. Mọi vectơ đều có một vectơ đơn vị dưới dạng các thành phần của nó.
5. Các vectơ đơn vị của một vectơ hướng dọc theo các trục.
6. Các vectơ đơn vị của một vectơ vuông góc với các vectơ đơn vị tương ứng của cùng một vectơ.

Vấn đề thực hành

1. Đối với một vectơ v đã cho, hãy kiểm tra xem vectơ đơn vị của nó có tồn tại hay không:      v = (1, 3)                v = (2, -1, 4)
2. Tìm vectơ đơn vị của vectơ sau:        v = (-2, -4, -4)
3. Tìm và chỉ ra bằng cách chứng minh vectơ đơn vị của vectơ sau:        v = (2, -5)
4. Tìm và chỉ ra bằng cách chứng minh vectơ đơn vị của vectơ sau:        v = (1, -1)
5. Tìm và chỉ ra bằng cách chứng minh vectơ đơn vị của vectơ sau:        v = (0, -4)

Câu trả lời

1. Vâng vâng
2. (-2/6, -4/6, -4/6)
3. Không
4. Đúng
5. Đúng

Xem thêm: