• Định nghĩa
• Eigenvectors
• Các giá trị riêng của ma trận vuông
• Tính chất
• Thí dụ
• Giá trị riêng của ma trận 2 × 2
• Vấn đề thực hành
• Câu hỏi thường gặp

Định nghĩa Eigenvalue

Giá trị riêng là tập hợp vô hướng đặc biệt liên quan đến hệ phương trình tuyến tính. Nó chủ yếu được sử dụng trong các phương trình ma trận. ‘Eigen’ là một từ tiếng Đức có nghĩa là ‘thích hợp’ hoặc ‘đặc điểm’. Do đó, thuật ngữ eigenvalue có thể được gọi là giá trị đặc trưng, ​​gốc đặc trưng, ​​giá trị thích hợp hoặc gốc tiềm ẩn. Nói một cách dễ hiểu, eigenvalue là một đại lượng vô hướng được sử dụng để biến đổi eigenvector. Phương trình cơ bản là

Ax = λx

Số hoặc giá trị vô hướng “ λ”  là giá trị riêng của A.

Trong Toán học, một eigenvector tương ứng với các giá trị riêng khác 0 thực hướng theo hướng được kéo dài bởi phép biến đổi trong khi giá trị eigen được coi là một hệ số mà nó được kéo dài. Trong trường hợp, nếu eigenvalue là âm, thì chiều chuyển đổi là âm.

Đối với mọi ma trận thực, có một giá trị riêng. Đôi khi nó có thể phức tạp. Sự tồn tại của giá trị riêng đối với ma trận phức là bằng định lý cơ bản của đại số.

EigenVectors là gì?

Eigenvector là các vectơ (khác 0) không thay đổi hướng khi bất kỳ phép biến đổi tuyến tính nào được áp dụng. Nó chỉ thay đổi bởi một hệ số vô hướng. Tóm lại, chúng ta có thể nói, nếu A là một phép biến đổi tuyến tính từ một không gian vectơ V và x là một vectơ trong V, không phải là một vectơ 0, thì v là một ký hiệu riêng của A nếu A (X) là một bội số vô hướng của x .

Một  Eigenspace  của vector x bao gồm một tập hợp tất cả các eigenvector có giá trị riêng tương đương gọi chung với vector zero. Mặc dù vậy, vectơ 0 không phải là một ký hiệu riêng.

Giả sử A là ma trận “n × n” và λ là giá trị riêng của ma trận A, khi đó x , một vector khác 0, được gọi là eigenvector nếu nó thỏa mãn biểu thức dưới đây;

A x  = λ x

x là một ký tự riêng của A tương ứng với giá trị riêng, λ.

Ghi chú :

• Có thể có vô số Eigenvectors, tương ứng với một giá trị riêng.
• Đối với các giá trị riêng biệt, các giá trị riêng phụ thuộc tuyến tính.

Các giá trị riêng của Ma trận vuông

Giả sử, A _{n × n} là ma trận vuông thì [A- λI] được gọi là ma trận Eigen hoặc ma trận đặc trưng, ​​là một vô hướng không xác định hoặc không xác định. Trong đó định thức của ma trận Eigen có thể được viết dưới dạng, | A- λI | và | A- λI | = 0 là phương trình Eigen hoặc phương trình đặc trưng, ​​trong đó “I” là ma trận nhận dạng . Các gốc của ma trận Eigen được gọi là các gốc Eigen.

Các giá trị riêng của ma trận tam giác và ma trận đường chéo tương đương với các phần tử trên đường chéo chính. Nhưng các giá trị riêng của ma trận vô hướng chỉ là giá trị vô hướng.

Thuộc tính của Eigenvalues

• Các Eigenvectors có Eigenvalues ​​Khác biệt Độc lập Tuyến tính
• Ma trận số ít có các giá trị riêng bằng 0
• Nếu A là ma trận vuông thì λ = 0 không phải là giá trị riêng của A
• Đối với bội vô hướng của ma trận: Nếu A là ma trận vuông và λ là giá trị riêng của A. Khi đó, aλ là giá trị riêng của aA.
• Đối với lũy thừa ma trận: Nếu A là ma trận vuông và λ là giá trị riêng của A và n≥0 là số nguyên thì λ ⁿ là giá trị riêng của A ⁿ .
• Đối với đa thức ma trận:  Nếu A là ma trận vuông, λ là giá trị riêng của A và p (x) là đa thức trong biến x thì p (λ) là giá trị riêng của ma trận p (A).
• Ma trận nghịch đảo: Nếu A là ma trận vuông, λ là giá trị riêng của A thì λ ^-1 là giá trị riêng của A ^-1
• Ma trận chuyển vị:  Nếu A là ma trận vuông, λ là giá trị riêng của A thì λ là giá trị riêng của A ^t

Ví dụ về EigenValue

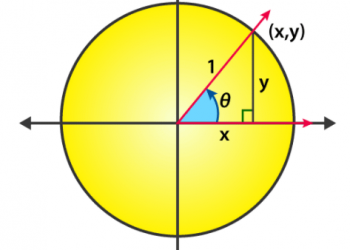
Trong ánh xạ cắt này, mũi tên màu xanh lam thay đổi hướng, trong khi mũi tên màu hồng thì không. Ở đây, mũi tên màu hồng là một dấu hiệu riêng vì nó không thay đổi hướng. Ngoài ra, chiều dài của mũi tên này không thay đổi; giá trị riêng của nó là 1.

Các giá trị riêng của Ma trận 2 x 2

Chúng ta hãy xem ví dụ dưới đây để biết cách tìm các giá trị riêng của ma trận 2 x 2.

Tìm các giá trị riêng của ma trận 2 x 2 .A = [03– 24]

Giải pháp:

Được,

A = [03– 24]

Sử dụng phương trình đặc trưng,

Đặt là ma trận nhận dạng 2 x 2.Tôi= [1001]

| A – λI | = 0

| [03– 24] –λ [1001] | =0| [03– 24] – [λ00λ] | =0∣∣∣– λ0– 24 – λ∣∣∣= 0

-λ (4 – λ) – (-2) (0) = 0

-4λ + λ ² = 0

λ (λ – 4) = 0

λ = 0 hoặc λ – 4 = 0

Do đó, λ = 0 hoặc λ = 4

Do đó, hai giá trị riêng của ma trận đã cho là λ = 0 và λ = 4.

Đi qua bài toán sau để tìm Eigenvalue của ma trận 3 x 3.

Thí dụ: 

Tìm Eigenvalue cho ma trậnA =⎡⎣⎢43– 2610– 61013– 8⎤⎦⎥

Giải pháp:

Ma trận đã cho:A =⎡⎣⎢43– 2610– 61013– 8⎤⎦⎥

Để tìm: Eigenvalues, λ i

Chúng ta biết rằng λ i là gốc của det (A-λI)

Trong đó, “Tôi” là Ma trận nhận dạng.

Do đó, det (A-λI) =∣∣∣∣⎡⎣⎢43– 2610– 61013– 8⎤⎦⎥– λ⎡⎣⎢100010001⎤⎦⎥∣∣∣∣

=∣∣∣∣⎡⎣⎢43– 2610– 61013– 8⎤⎦⎥–⎡⎣⎢λ000λ000λ⎤⎦⎥∣∣∣∣

Vì thế,

det (A-λI) =∣∣∣∣4 – λ3– 2610 – λ– 61013– 8 – λ∣∣∣∣

= ( 4 – λ )∣∣∣10 – λ– 613( – 8 – λ )∣∣∣– ( 6 )∣∣∣3– 213– 8 – λ∣∣∣+ 10∣∣∣3– 210 – λ– 6∣∣∣

= ( 4 – λ ) [ ( 10 – λ ) ( – 8 – λ ) – 13 ( – 6 ) ] – 6 [ ( 3 ) ( – 8 – λ ) – 13 ( – 2 ) ]+ 10 [ ( 3 ) ( – 6 ) – ( 10 – λ ) ( – 2 ) ]

Bây giờ, lấy phần đầu tiên từ phương trình trên.

=( 4 – λ ) [ – 80 – 10 λ + 8 λ +λ2+ 78 ]

=( 4 – λ ) [ – 2 – 2 λ +λ2]

Khi đơn giản hóa biểu thức trên, chúng ta nhận được

= – 8 – 8 λ + 4λ2+ 2 λ + 2λ2–λ3

= –λ3+ 6λ2– 6 λ – 8 , là dạng đơn giản của số hạng đầu tiên của biểu thức. … (1)

Tương tự, đối với số hạng thứ hai của phương trình, chúng ta nhận được

=– 6 [ – 24 – 3 λ + 26 ]

=– 6 [ 2 – 3 λ ]

= … (2)– 12 + 18 λ

Tương tự đối với thuật ngữ thứ ba,

=10 [ – 18 – ( 20 + 2 λ ) ] = 10 [ – 18 + 20 – 2 λ ]

=10 ( 2 – 2 λ )

= … (3)20 – 20 λ

Vì thế,

det (A-λI) = (1) + (2) + (3)

det (A-λI) = -λ ³ + 6λ ² – 6λ – 8 – 12 + 18λ + 20-20λ

= -λ ³ + 6λ ² -8λ + 0

Do đó, các giá trị riêng của ma trận A có thể được tìm thấy bằng

-λ ³ + 6λ ² -8λ = 0

Bây giờ, nhân phương trình trên với (-1) ở cả hai vế, chúng ta nhận được

λ ³ -6λ ² + 8λ = 0

Khi tính toán phương trình trên, chúng ta nhận được

λ (λ ² -6λ + 8) = 0

Vì vậy,

λ = 0 và (λ ² -6λ + 8) = 0

Sử dụng công thức phương trình bậc hai, để tìm nghiệm nguyên của phương trình (λ ² -6λ + 8) = 0

Ở đây, a = 1, b = -6, c = 8

Bây giờ, các giá trị trong công thức bậc hai,

=6 ±36 – 4 ( 1 ) ( 8 )√2 ( 1 )

=6 ±36 – 32√2

=6 ± 22

Do đó, λ = 2 và λ = 4

Do đó, các Giá trị riêng của ma trận A là 0, 2, 4.

Vấn đề thực hành

Tìm Eigenvalues ​​cho các Ma trận sau.

• A =⎡⎣⎢2131233320⎤⎦⎥
• A =⎡⎣⎢124731461⎤⎦⎥