Giá trị tuyệt đối – Thuộc tính & Ví dụ đơn giản nhất

Giá trị tuyệt đối là gì?

Giá trị tuyệt đối đề cập đến khoảng cách của một điểm từ 0 hoặc điểm gốc trên trục số, bất kể hướng. Giá trị tuyệt đối của một số luôn dương.

Giá trị tuyệt đối của một số được biểu thị bằng hai đường thẳng đứng bao quanh số hoặc biểu thức. Ví dụ, giá trị tuyệt đối của số 5 được viết là, | 5 | = 5. Điều này có nghĩa là, khoảng cách từ 0 là 5 đơn vị:

Tương tự, giá trị tuyệt đối của âm 5 được biểu thị là, | -5 | = 5. Điều này có nghĩa là, khoảng cách từ 0 là 5 đơn vị:

Một số không chỉ hiển thị khoảng cách từ điểm gốc mà còn rất quan trọng để vẽ đồ thị giá trị tuyệt đối.

Xét một biểu thức | x | > 5. Để biểu diễn điều này, trên một trục số, bạn cần tất cả các số có giá trị tuyệt đối lớn hơn 5. Điều này được thực hiện bằng đồ thị bằng cách đặt một dấu chấm mở trên trục số.

Hãy xem xét một trường hợp khác trong đó | x | = 5. Điều này bao gồm tất cả các giá trị tuyệt đối nhỏ hơn hoặc bằng 5. Biểu thức này được vẽ đồ thị bằng cách đặt một dấu chấm đóng trên trục số. Dấu bằng chỉ ra rằng tất cả các giá trị đang được so sánh đều được đưa vào biểu đồ.

Một cách dễ dàng để biểu diễn biểu thức với các bất đẳng thức là tuân theo các quy tắc sau.

• Đối với | x| <5, -5 <  x  <5
• Đối với | x| = 5, -5 =  x  = 5
• Đối với | x + 6 | <5, -5 <  x+ 6 <5

Thuộc tính của giá trị tuyệt đối

Giá trị tuyệt đối có các thuộc tính cơ bản sau:

1. Phi phủ định | a | ≥ 0
2. Tính xác định dương | a | = 0a = 0
3. Tính nhân | ab | = | a | | b |
4. Độ nhạy cảm phụ | a + b | ≤ | a | + | b |
5. Sự lý tưởng || a || = | a |
6. Phép đối xứng | −a | = | a |
7. Nhận dạng không thể phân biệt | a – b | = 0 ⇔ a = b
8. Bất đẳng thức tam giác | a – b | ≤ | a – c | + | c – b |
9. Bảo toàn phép chia | a / b | = | a | / | b | nếu b ≠ 0

ví dụ 1

Đơn giản hóa – | -6 |

Giải pháp

• Chuyển các ký hiệu giá trị tuyệt đối thành dấu ngoặc đơn

– | –6 | = – (6)

• Bây giờ tôi có thể lấy phủ định qua dấu ngoặc đơn:

– (6) = – 6

Ví dụ 2

Tìm các giá trị có thể có của x.

| 4x | = 16

Giải pháp

Trong phương trình này, 4x có thể là số dương hoặc số âm. Vì vậy, chúng ta có thể viết nó là:

4x = 16 hoặc -4x = 16

Chia cả hai bên cho 4.

x = 4 hoặc x = -4

Do đó, hai giá trị có thể có của x là -4 và 4.

Ví dụ 3

Giải quyết các vấn đề sau:

a) Giải quyết | –9 |

Câu trả lời

| –9 | = 9

b) Đơn giản hóa | 0 – 8 |.

Câu trả lời

| 0 – 8 | = | –8 | = 8

1. c) Giải quyết | 9 – 3 |.

Câu trả lời

| 9 – 3 | = | 6 | = 6

1. d) Đơn giản hóa | 3 – 7 |.

Câu trả lời

| 3 – 7 | = | –4 | = 4

e) Tập luyện | 0 (–12) |.

Câu trả lời

| 0 (–12) | = | 0 | = 0

f) Đơn giản hóa | 6 + 2 (–2) |.

Câu trả lời

| 6 + 2 (–2) | = | 6 – 4 | = | 2 | = 2

1. g) Giải quyết – | –6 |.

Câu trả lời

– | –6 | = – (6) = –6

h) Đơn giản hóa – | (–7) ²|.

Câu trả lời

– | (–7) ²  | = – | 49 | = –49

1. i) Tính – | –9 | ²

Câu trả lời

– | –9 | ²  = – (9) ²  = – (4) = –81

j) Rút gọn (- | –3 |) ².

Câu trả lời

(- | –3 |) ²  = (- (3)) ²  = (–3) ²  = 9

Ví dụ 4

Đánh giá: – | -7 + 4 |

Giải pháp

• Trước hết, hãy bắt đầu bằng cách tính ra các biểu thức trong các ký hiệu giá trị tuyệt đối:
  – | -7 + 4 | = – | -3 |
• Giới thiệu dấu ngoặc
  – | -3 | = – (3) = -3
• Vì vậy, câu trả lời là -3.

Ví dụ 5

Một thợ lặn biển ở độ sâu -20 feet so với mặt nước. Anh ta cần bơi bao xa để lên mặt nước?

Giải pháp

Anh ấy cần bơi | -20 | = 20 bộ.

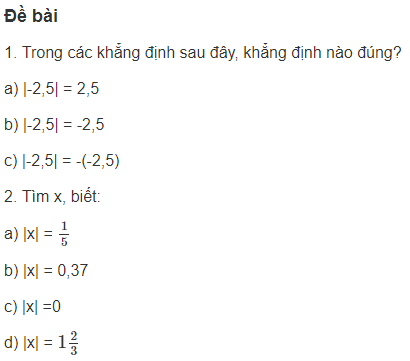
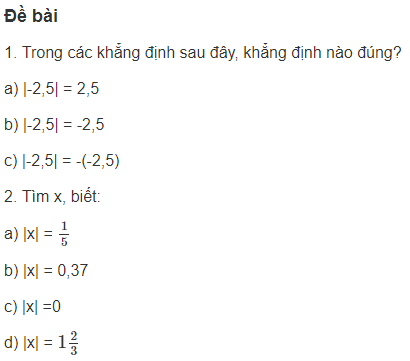
Ví dụ 6

Tính giá trị tuyệt đối của 19 – 36 (3) + 2 (4 – 87)?

Giải pháp

19 – 36 (3) + 2 (4 – 87)

= 19 – 108 + 2 (-83)

= 19 – 108 – 166

= -255

Ví dụ 7

Giải phương trình bằng cách xác định các giá trị tuyệt đối,

2 | -2 × – 2 | – 3 = 13

Giải pháp

Viết lại biểu thức có dấu giá trị tuyệt đối về một phía.

• Thêm 3 vào cả hai bên của biểu thức

2 | – 2 × – 2 | – 3 + 3 = 13 + 3

2 | – 2 × – 2 | = 16

• Chia cả hai bên cho 2.

| – 2 × – 2 | = 8

• Phương trình còn lại tương tự như viết biểu thức dưới dạng:

– 2 × – 2 = 8 hoặc – 8

1. a) -2 x – 2 = 8

Bây giờ giải cho x
x = – 5

1. b) – 2 x – 2 = – 8

x = 3

• Câu trả lời đúng là (-5, 3).

Xem thêm:

Cách tính căn bậc hai của một số nhanh gọn đơn giản nhất

Chuỗi số là gì? Tìm hiểu những thông tin mới nhất về nó

Ví dụ 8

Tính các giá trị thực để biểu thức có giá trị tuyệt đối.

| x – 1 | = 2x + 1

Giải pháp

Một phương pháp giải phương trình này là xét hai trường hợp:
a) Giả sử x – 1 ≥ 0 và viết lại biểu thức dưới dạng:

x – 1 = 2x + 1

Tính giá trị của x
x = -2
b) Giả sử x – 1 ≤ 0 và viết lại biểu thức này thành
– (x – 1) = 2x + 1
– x + 1 = 2x + 1
tìm x là
x = 0

Điều quan trọng là phải kiểm tra xem các nghiệm có đúng với phương trình hay không vì tất cả các giá trị của x đã được giả định.
Thay x bằng – 2 vào cả hai vế của biểu thức ta được.

| (-2) – 1 | = | -2 + 1 | = 1 ở phía bên trái và 2 (-2) + 1 = – 3 ở phía bên phải

Vì hai phương trình không bằng nhau, do đó x = -2 không phải là một đáp số cho phương trình này.
Kiểm tra x = 0

Thay x bằng 0 ở cả hai vế của phương trình sẽ cho kết quả:

| (0) – 1 | = 1 ở bên trái và 2 (0) + 1 = 1 ở bên phải.

Hai biểu thức bằng nhau và do đó, x = 0 là nghiệm của phương trình này.