Giải Hệ thống Bất đẳng thức Tuyến tính dễ hiểu nhất

Giải Hệ thống Bất đẳng thức Tuyến tính

Từ bất đẳng thức đơn giản có nghĩa là một biểu thức toán học trong đó các cạnh không bằng nhau.

Về cơ bản, có năm ký hiệu bất đẳng thức được sử dụng để biểu diễn các phương trình bất đẳng thức.

Đó là: nhỏ hơn (<), lớn hơn (>), nhỏ hơn hoặc bằng (≤), lớn hơn hoặc bằng (≥) và ký hiệu không bằng (≠). Bất đẳng thức được sử dụng để so sánh giữa các số và xác định phạm vi hoặc phạm vi giá trị thỏa mãn các điều kiện của một biến nhất định.

Hệ thống bất bình đẳng tuyến tính là gì?

Hệ bất phương trình tuyến tính là một tập hợp các phương trình bất phương trình tuyến tính chứa các biến giống nhau.

Một số phương pháp giải hệ phương trình tuyến tính chuyển sang hệ bất phương trình tuyến tính. Tuy nhiên, việc giải hệ bất phương trình tuyến tính có phần khác với hệ phương trình tuyến tính vì các dấu hiệu bất đẳng thức cản trở chúng ta giải bằng phương pháp thay thế hoặc loại bỏ. Có lẽ phương pháp tốt nhất để giải các hệ bất phương trình tuyến tính là vẽ đồ thị các bất phương trình.

Xem thêm:

Bất đẳng thức về giá trị tuyệt đối – Giải thích & Ví dụ

Giải bất phương trình bậc hai – Giải thích & Ví dụ

Làm thế nào để giải các hệ thống bất bình đẳng tuyến tính?

Trước đây, bạn đã học cách giải một bất phương trình tuyến tính đơn bằng cách vẽ đồ thị. Trong bài này, chúng ta sẽ học cách tìm nghiệm cho một hệ bất phương trình tuyến tính bằng cách vẽ đồ thị đồng thời hai hay nhiều bất phương trình tuyến tính.

Giải pháp cho một hệ bất phương trình tuyến tính là vùng mà đồ thị của tất cả các bất phương trình tuyến tính trong hệ trùng nhau.

Để giải một hệ bất phương trình, hãy vẽ đồ thị của mỗi bất phương trình tuyến tính trong hệ trên cùng một trục xy theo các bước sau :

• Cô lập biến y trong mỗi bất đẳng thức tuyến tính.
• Vẽ và tô bóng vùng phía trên đường viền bằng cách sử dụng nét đứt và nét liền cho các ký hiệu> và ≥ tương ứng.
• Tương tự, vẽ và tô bóng vùng bên dưới đường viền bằng cách sử dụng nét đứt và nét liền cho các ký hiệu <và ≤ tương ứng.
• Làm bóng vùng mà tất cả các phương trình trùng nhau hoặc giao nhau. Và nếu không có miền nào là giao điểm thì ta kết luận hệ bất phương trình không có nghiệm.

Hãy xem qua một vài ví dụ để hiểu các bước này.

ví dụ 1

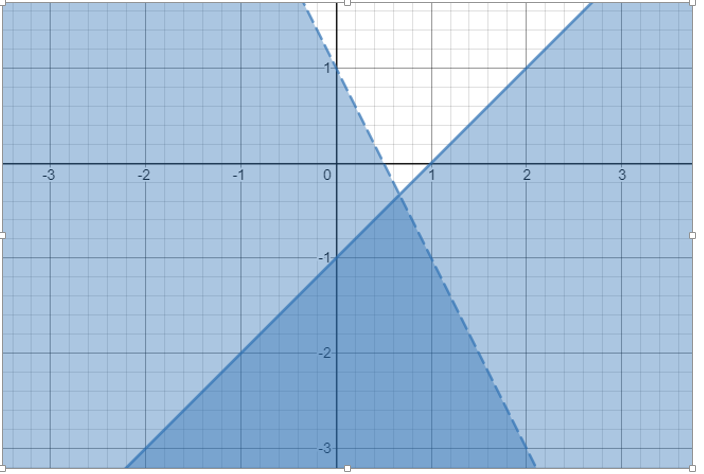
Vẽ đồ thị của hệ bất phương trình tuyến tính sau:

y ≤ x – 1 và y <–2x + 1

Giải pháp

Vẽ đồ thị của bất phương trình bậc nhất y ≤ x – 1.

• Vì biểu tượng “nhỏ hơn hoặc bằng”, sẽ vẽ một đường viền liền và tô bóng bên dưới đường kẻ.
• Đồng thời vẽ đồ thị của bất phương trình thứ hai y <–2x + 1 trên cùng một trục xy.
• Trong trường hợp này, đường biên giới của chúng ta sẽ bị đứt đoạn hoặc có dấu chấm do ký hiệu nhỏ hơn. Che bóng khu vực bên dưới đường viền.

Do đó, giải pháp cho hệ thống bất đẳng thức này là vùng bóng mờ tối hơn được mở rộng vĩnh viễn theo hướng đi xuống như hình dưới đây.

Ví dụ 2

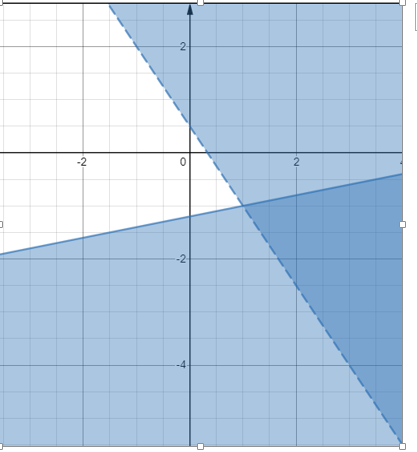
Giải hệ bất phương trình sau:

x – 5y ≥ 6

3x + 2y> 1

Giải pháp

• Đầu tiên, cô lập biến y ở bên trái trong mỗi bất đẳng thức.

Với x – 5y ≥ 6;

=> x ≥ 6 + 5y

=> 5y ≤ x – 6

=> y ≤ 0,2 x  – 1,2

Và cho 3x + 2y> 1;

=> 2y> 1 – 3x

=> y> 0,5 – 1,5x

• Chúng ta sẽ vẽ biểu đồ y ≤ 2 x– 1.2 và y> 0.5 – 1.5x bằng cách sử dụng một đường liền nét và một đường đứt quãng.

Nghiệm của hệ bất phương trình là vùng được tô đậm hơn, là vùng chồng lấn của hai vùng nghiệm riêng lẻ.

Ví dụ 3

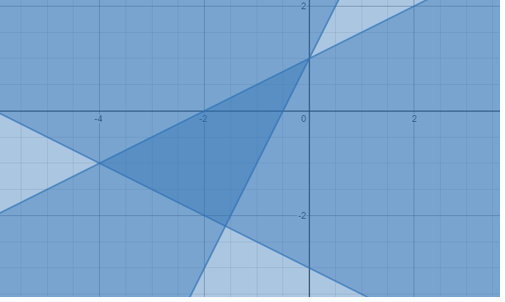
Vẽ đồ thị của hệ bất phương trình tuyến tính sau đây.

y ≤ (1/2) x + 1,

y ≥ 2x – 2,

y ≥ – (1/2) x – 3.

Giải pháp

Hệ bất phương trình này có ba phương trình được nối với nhau bằng ký hiệu “bằng”. Điều này cho chúng ta biết rằng tất cả các đường biên giới sẽ vững chắc. Đồ thị của ba bất phương trình được hiển thị bên dưới.

Vùng bóng mờ của ba phương trình chồng lên nhau ngay trong phần giữa. Do đó, các nghiệm của hệ thống, nằm trong vùng giới hạn như thể hiện trên đồ thị.

Ví dụ 4

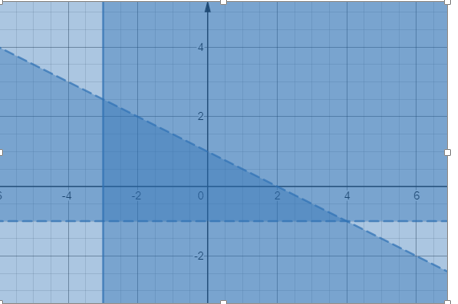
Vẽ đồ thị của hệ bất phương trình tuyến tính sau:

x + 2y <2, y> –1,

x ≥ –3.

Giải pháp

Cô lập biến y trong bất phương trình bậc nhất nhận được;

y <- x / 2 +1 Bạn cần lưu ý rằng bất phương trình y> –1 và x ≥ –3 sẽ có các đường biên ngang và dọc tương ứng. Hãy vẽ đồ thị của ba bất đẳng thức như minh họa bên dưới.

Vùng bóng mờ tối hơn được bao quanh bởi hai đoạn thẳng chấm và một đoạn liền nét sẽ đưa ra nghiệm của ba bất phương trình.

Ví dụ 5

Giải hệ bất phương trình tuyến tính sau:

–2x -y <-1

4x + 2y ≤-6

Giải pháp

Cô lập biến y trong mỗi bất đẳng thức.

–2x -y <-1 => y> –2x + 1

4x + 2y ≤ -6 => y ≤ -2x -3

Hãy tiếp tục và vẽ đồ thị y> –2x + 1 và y ≤ -2x -3:

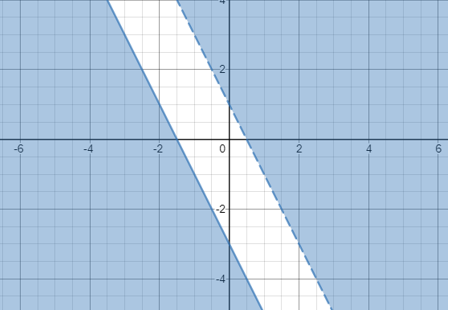
Vì vùng tô bóng của hai bất phương trình không trùng nhau, do đó chúng ta có thể kết luận rằng hệ bất phương trình không có nghiệm.