Giải phương trình nhiều bước nhanh chóng dễ hiểu

Giải phương trình nhiều bước – Phương pháp & ví dụ

Để hiểu cách lập phương trình nhiều bước , người ta phải có một nền tảng vững chắc về cách giải phương trình một bước và hai bước. Và vì lý do này, chúng ta hãy xem xét ngắn gọn về những gì mà phương trình một bước và hai bước đòi hỏi.

Phương trình một bước là phương trình chỉ cần một bước để giải. Bạn chỉ thực hiện một thao tác duy nhất để giải quyết hoặc cô lập một biến. Ví dụ về phương trình một bước bao gồm: 5 + x = 12, x – 3 = 10, 4 + x = -10, v.v.

• Ví dụ, để giải quyết 5 + x = 12,

Bạn chỉ cần trừ 5 cho cả hai vế của phương trình

5 + x = 12 => 5 – 5 + x = 12 – 5

=> x = 7

• 3x = 12

Để giải phương trình này, hãy chia cả hai vế của phương trình cho 3.

x = 4

Bạn có thể lưu ý rằng để một phương trình một bước được giải quyết hoàn toàn, bạn chỉ cần một bước duy nhất, đó là cộng / trừ hoặc nhân / chia.

Mặt khác, phương trình hai bước là phương trình yêu cầu thực hiện hai phép toán để giải hoặc cô lập một biến. Trong trường hợp này, các phép toán để giải quyết một hai bước là cộng hoặc trừ và nhân hoặc chia. Ví dụ về phương trình hai bước là:

• (x / 5) – 6 = -8

Giải pháp

Cộng cả 6 vào cả hai vế của phương trình và nhân với 5.

(x / 5) – 6 + 6 = – 8 + 6

(x / 5) 5 = – 2 x 5

x = -10

• 3y – 2 = 13

Giải pháp

Cộng 2 vào cả hai vế của phương trình và chia cho 3.

3y – 2 + 2 = 13 + 2

3 năm = 15

3y / 3 = 15/3

y = 5

• 3x + 4 = 16.

Giải pháp

Để giải phương trình này, hãy trừ 4 cho cả hai vế của phương trình,

3x + 4 – 4 = 16 – 4.

Điều này cho bạn phương trình một bậc 3x = 12. Chia cả hai vế của phương trình cho 3,

3x / 3 = 12/3

x = 4

Phương trình nhiều bước là gì?

Thuật ngữ “đa” có nghĩa là nhiều hoặc nhiều hơn hai, do đó, một phương trình nhiều bước có thể được định nghĩa là một biểu thức đại số yêu cầu một số phép toán cộng, trừ, chia và lũy thừa để giải. Phương trình nhiều bước được giải bằng cách áp dụng các kỹ thuật tương tự được sử dụng trong giải phương trình một bước và hai bước.

Giống như chúng ta đã thấy trong phương trình một bước và hai bước, mục tiêu chính của việc giải phương trình nhiều bước cũng là cô lập biến chưa biết trên RHS hoặc LHS của phương trình trong khi giữ một số hạng không đổi ở phía đối diện. Chiến lược thu được một biến có hệ số bằng một đòi hỏi một số quá trình.

Quy luật phương trình là quy tắc quan trọng nhất mà bạn nên nhớ khi giải bất kỳ phương trình tuyến tính nào. Điều này ngụ ý rằng, bất cứ điều gì bạn làm với một vế của phương trình, bạn PHẢI làm ngược lại với phương trình.

Ví dụ, nếu bạn cộng hoặc trừ một số ở một vế của phương trình, bạn cũng phải cộng hoặc trừ ở vế đối của phương trình.

Làm thế nào để giải các phương trình nhiều bước?

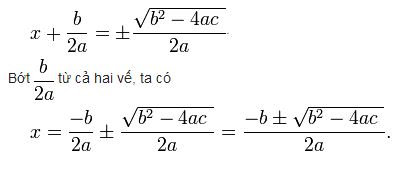
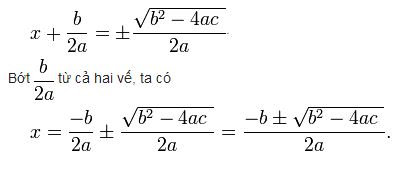
Một biến trong phương trình có thể được cô lập ở bất kỳ phía nào tùy thuộc vào sở thích của bạn. Tuy nhiên, giữ một biến ở bên trái của phương trình có ý nghĩa hơn vì một phương trình luôn được đọc từ trái sang phải.

Khi giải các biểu thức đại số , bạn cần lưu ý rằng không nhất thiết phải có một biến là x. Phương trình đại số sử dụng bất kỳ chữ cái có sẵn nào.

Tóm lại, để giải các phương trình nhiều bước, cần tuân theo các quy trình sau:

• Loại bỏ bất kỳ ký hiệu nhóm nào như dấu ngoặc đơn, dấu ngoặc nhọn và dấu ngoặc nhọn bằng cách sử dụng thuộc tính phân phối của phép nhân hơn phép cộng.
• Đơn giản hóa cả hai vế của phương trình bằng cách kết hợp các số hạng.
• Cô lập một biến ở bất kỳ vế nào của phương trình tùy thuộc vào sở thích của bạn.
• Một biến được tách biệt thực hiện hai phép toán đối lập nhau như cộng và trừ. Phép cộng và phép trừ là hoạt động đối lập của phép nhân và phép chia.

Ví dụ về cách giải phương trình nhiều bước

ví dụ 1

Giải phương trình nhiều bước dưới đây.

12x + 3 = 4x + 15

Giải pháp

Đây là một phương trình nhiều bước điển hình trong đó các biến nằm ở cả hai phía. Phương trình này không có ký hiệu nhóm và giống như các thuật ngữ để kết hợp trên các cạnh đối diện. Bây giờ, để giải phương trình này, trước tiên hãy quyết định nơi giữ biến. Vì 12x ở phía bên trái lớn hơn 4x ở phía bên phải, do đó chúng tôi giữ nguyên biến số của chúng tôi đối với LHS của phương trình.

Điều này ngụ ý rằng, chúng tôi trừ đi 4x cho cả hai vế của phương trình

12x – 4x + 3 = 4x – 4x + 15

6x + 3 = 15

Cũng trừ cả hai bên đi 3.

6x + 3 – 3 = 15 – 3

6x = 12

Bước cuối cùng bây giờ là tách x bằng cách chia cả hai vế cho 6.

6x / 6 = 12/6

x = 2

Và ở đó, chúng tôi đã hoàn thành!

Ví dụ 2

Giải cho x trong phương trình nhiều bước dưới đây.

-3x – 32 = -2 (5 – 4x)

Giải pháp

• Bước đầu tiên là loại bỏ dấu ngoặc đơn bằng cách sử dụng Thuộc tính phân phối của phép nhân.

-3x – 32 = -2 (5 – 4x) = -3x – 32 = – 10 + 8x

• Trong ví dụ này, chúng tôi đã quyết định giữ biến ở bên trái.
• thêm cả hai cạnh của 3x cho; -3x + 3x – 32 = – 10 + 8x + 3x =>

– 10 + 11x = -32

• Cộng cả hai vế của phương trình với 10 để xóa -10.

– 10 + 10 + 11x = -32 + 10

11x = -22

• Cô lập biến xbằng cách chia cả hai vế của phương trình cho 11.

11x / 11 = -22/11

x = -2

Ví dụ 3

Giải phương trình nhiều bậc 2 (y −5) = 4y + 30.

Giải pháp

• Bỏ dấu ngoặc bằng cách phân phối số ra bên ngoài.

= 2y -10 = 4y + 30

• Bằng cách giữ biến ở vế phải, trừ 2y cho cả hai vế của phương trình.

2y – 2y – 10 = 4y – 2y + 23

-10 = 2y + 30

• Tiếp theo, trừ cả hai vế của phương trình đi 30.

-10 – 30 = 2y + 30 – 30

– 40 = 2 năm

• Bây giờ chia cả hai vế cho hệ số của 2y để nhận giá trị của y.

-40/2 = 2y / 2

y = -20

Ví dụ 4

Giải phương trình nhiều bước dưới đây.

8x -12x -9 = 10x – 4x + 31

Giải pháp

• Đơn giản hóa phương trình bằng cách kết hợp các số hạng giống như ở cả hai bên.

– 4x – 9 = 6x +31

• Trừ đi 6x trên cả hai vế của phương trình để biến x nằm ở vế trái của phương trình.

– 4x -6x – 9 = 6x -6x + 31

-10x – 9 = 31

• Thêm 9 vào cả hai vế của phương trình.

– 10x -9 + 9 = 31 +9

-10x = 40

• Cuối cùng, chia cả hai bên cho -10 để có được giải pháp.

-10x / -10 = 40 / -10

x = – 4

Ví dụ 5

Giải cho x trong phương trình nhiều bước 10x – 6x + 17 = 27 – 9

Giải pháp

Kết hợp các điều khoản tương tự trên cả hai vế của phương trình

4x + 17 = 18

Trừ 17 cho cả hai bên.

4x + 17 – 17 = 18 -17

4x = 1

Cô lập x bằng cách chia cả hai vế cho 4.

4x / 4 = 1/4

x = 1/4

Ví dụ 6

Giải cho x trong phương trình nhiều bước dưới đây.

-3x – 4 (4x – 8) = 3 (- 8x – 1)

Giải pháp

Bước đầu tiên là loại bỏ các dấu ngoặc bằng cách nhân số bên ngoài dấu ngoặc với các số hạng trong dấu ngoặc.

-3x -16x + 32 = -24x – 3

Thực hiện một chút dọn dẹp nhà cửa bằng cách thu thập các thuật ngữ giống như ở cả hai bên của phương trình.

-19x + 32 = -24x – 3

Hãy giữ biến của chúng ta ở bên trái bằng cách thêm 24x vào cả hai vế của phương trình.

-19 + 24x + 32 = -24x + 24x – 3

5x + 32 = 3

Bây giờ di chuyển tất cả các hằng số sang phía bên phải bằng cách trừ đi 32.

5x + 32 -32 = -3 -32

5x = -35

Bước cuối cùng là chia cả hai vế của phương trình cho 5 để cô lập x.

5x / 5 = – 35/5

x = -7

Ví dụ 7

Giải cho t trong phương trình nhiều bước dưới đây.

4 (2t – 10) – 10 = 11 – 8 (t / 2 – 6)

Giải pháp

Áp dụng tính chất phân phối của phép nhân để loại bỏ dấu ngoặc.

8t -40 – 10 = 11 -4t – 48

Kết hợp các điều khoản tương tự trên cả hai vế của phương trình.

8t -50 = -37 – 4t

Hãy giữ biến ở vế trái bằng cách cộng 4t vào cả hai vế của phương trình.

8t + 4t – 50 = -37 – 4t + 4t

12t – 50 = -37

Bây giờ thêm 50 vào cả hai vế của phương trình.

12t – 50 + 50 = – 37 + 50

12t = 13

Chia cả hai vế cho 12 để cô lập t.

12t / 12 = 13/12

t = 13/12

Ví dụ 8

Giải cho w trong phương trình nhiều bước sau đây.

-12w -5-9 + 4w = 8w – 13w + 15 – 8

Giải pháp

Kết hợp số hạng tương tự và các hằng số của cả hai vế của phương trình.

-8w – 14 = -5w + 7

Để giữ biến ở phía bên trái, chúng tôi thêm 5w ở cả hai bên.

-8w + 5w – 14 = -5w + 5w + 7

-3w – 14 = 7

Bây giờ thêm 14 vào cả hai vế của phương trình.

– 3w – 14 + 14 = 7 + 14

-3w = 21

Bước cuối cùng là chia cả hai vế của phương trình cho -3

-3w / -3 = 21/3

w = 7.

Xem thêm:

Giải phương trình giá trị tuyệt đối nhanh chóng nhất

Giải phương trình hai bước – Kỹ thuật & ví dụ đơn giản nhất

Câu hỏi thực hành

Giải các phương trình nhiều bước sau:

1. 5 + 14x = 9x – 5
2. 7 (2y – 1) – 11 = 6 + 6y
3. 4b + 5 = 1 + 5b
4. 2 ( x + 1) –  x  = 5
5. 16 = 2 (x – 1) – x
6. 5x – 0,2 (x – 4,2) = 1,8
7. 9 (x – 2) = 3x + 3
8. 2y + 1 = 2x – 3.
9. 6 x  – (3 x  + 8) = 16
10. 13 – (2 x + 2) = 2 ( x  + 2) + 3 x
11. 2 [3 x  + 4 (3 –  x )] = 3 (5 – 4 x ) – 11
12. 3 [ x – 2 (3 x  – 4)] + 15 = 5 – [2 x  – (3 +  x )] – 11
13. 7 (5 x  – 2) = 6 (6 x  – 1)
14. 3 (x + 5) = 2 (−6 – x) −2x