Giống như phân số
Nhóm của hai hay nhiều phân số có cùng mẫu số được gọi là phân số giống nhau. Hoặc chúng ta có thể nói rằng các phân số có cùng số ở mẫu số được gọi là phân số. Ví dụ, 1/7, 2/7, 5/7, 6/7 đều giống như phân số, có mẫu số bằng 7.


Có thể dễ dàng thực hiện các phép tính số học như cộng và trừ như phân số. Chúng ta không cần phải trung hòa các mẫu số trong khi thực hiện cả hai phép toán. Hãy để chúng tôi hiểu với sự trợ giúp của các ví dụ.
Phép cộng và phép trừ các phân số giống như
Khi chúng ta cộng hoặc trừ các phân số tương tự, mẫu số sẽ không đổi và chỉ các tử số được cộng hoặc trừ tương ứng. Dưới đây là các ví dụ.
Ví dụ 1: Thêm 2/3 và 5/3
Bài giải: 2/3 + 5/3 = (2 + 5) / 3 = 7/3
Ví dụ 2: Trừ 1/2 cho 11/2.
Bài giải: 11/2 – 1/2 = (11-1) / 2 = 10/2 = 5
Những điểm cần nhớ
- 2/4, 4/8, 1/2, v.v. không giống như phân số, mặc dù khi được đơn giản hóa, chúng đều cho kết quả là 1/2.
- 6/16 và 6/26 không giống như phân số. Các tử số giống nhau, nhưng mẫu số thì không.
- 2, 3, 4 giống như phân số vì mẫu số của chúng được coi là 1, có nghĩa là các phân số này là 2/1, 3/1 và 4/1.
Không giống như phân số
Các phân số có mẫu số khác nhau được gọi là phân số không giống nhau. Ở đây mẫu số của các phân số có các giá trị khác nhau. Ví dụ, 2/3, 4/9, 6/67, 9/89 không giống như phân số.
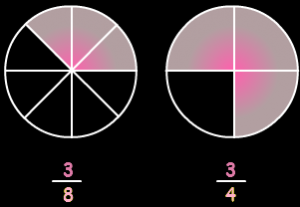

Không giống như phân số
Vì các mẫu số ở đây là khác nhau, do đó không dễ dàng để cộng hoặc trừ các phân số như vậy. Để thực hiện các phép toán số học như cộng và trừ, trước tiên chúng ta phải chuyển các phân số không giống nhau thành phân số giống. Sau đó, chúng tôi thực hiện các hoạt động cần thiết.
Phép cộng và phép trừ các phân số không giống như
Khi chúng ta cộng và trừ hai phân số không giống nhau, chúng ta phải làm cho mẫu số bằng nhau trước rồi thực hiện phép toán tương ứng. Có hai phương pháp mà chúng ta có thể làm cho mẫu số bằng nhau. Họ đang:
- Phương pháp nhân chéo
- Phương pháp LCM
Trong phương pháp nhân chéo , chúng ta nhân chéo tử số của phân số thứ nhất với mẫu số của phân số thứ hai. Sau đó nhân tử số của phân số thứ hai với mẫu số của phân số thứ nhất. Bây giờ, nhân cả hai mẫu số và lấy nó làm mẫu số chung. Sau đó, chúng ta có thể cộng hoặc trừ các phân số ngay bây giờ.
Ví dụ: Thêm 1/3 và 3/4
Giải pháp: 1/3 + 3/4
Bằng phương pháp nhân chéo, ta nhận được;
= [(1 x 4) + (3 x 3)] / 3 x 4
= (4 + 9) / 12
= 13/12
Trong phương pháp LCM , trước tiên, chúng ta cần lấy LCM của các mẫu số của các phân số đã cho. Bây giờ sử dụng LCM này, hãy biến tất cả các phân số giống như phân số. Sau đó, chúng ta có thể đơn giản hóa tử số.
Ví dụ: Thêm 3/8 và 5/12
Giải pháp: 3/8 + 5/12
Bây giờ lấy LCM của 8 và 12, chúng tôi nhận được;
LCM (8, 12) = 2 x 2 x 2 x 3 = 24
Bây giờ nhân các phân số đã cho để được các mẫu số bằng 24, sao cho;
= [(3 x 3) / (8 x 3)] + [(5 x 2) + (12 x 2)]
= (24/9) + (24/10)
= (9 + 10) / 24
= 19/24.
Chuyển đổi Phân số Không thích thành Phân số Thích
Giống như phân số tạo điều kiện thuận lợi cho việc so sánh các phân số. Vì vậy, thường có nhu cầu chuyển đổi không giống như phân số sang chúng.
Hãy để chúng tôi chuyển đổi 1, 4/5, 7/10 và 1/2 thành như phân số. Các bước chuyển đổi:
- Tìm LCM của các mẫu số. LCM của 1, 5, 10 và 2 là 10.
- Tính các phân số tương đương của chúng có cùng mẫu số, tức là LCM.
1/1 = (1 × 10) / (1 × 10) = 10/10
4/5 = (4 × 2) / (5 × 2) = 8/10
7/10 = (7 × 1) / (10 × 1) = 7/10
1/2 = (1 × 5) / (2 × 5) = 5/10
1, 4/5, 7/10 và 1/2 không giống như phân số, có thể được biểu diễn dưới dạng 10/10, 8/10, 7/10 và 5/10 giống như phân số.
Cần lưu ý rằng khi các mẫu số trở nên bằng nhau, các phân số có thể được so sánh. Bạn sẽ không thể trả lời lớn nhất trong số 1, 4/5, 7/10 và 1/2. Nhưng khi chúng đã được chuyển đổi thành 10/10, 8/10, 7/10 và 5/10, bạn có thể sắp xếp chúng theo thứ tự tăng dần là 5/10, 7/10, 8/10 và 10/10 rất tiện lợi.
Các loại phân số
Chủ yếu có ba loại phân số, chúng là:
- Phần thích hợp
- Phân số không đúng
- Phân số hỗn hợp
Phân số đúng và không đúng
Tương tự như phân số giống và không giống như phân số, chúng ta có một loại phân số khác, được gọi là phân số đúng và không đúng.
- Một phần thích hợp là một phần nhỏ mà có một giá trị nhỏ hơn 1. Hoặc chúng ta có thể nói, khi giá trị của tử số nhỏ hơn mẫu số, sau đó phân số như vậy được gọi là phân số-cho phù hợp ví dụ, 1/2, 1/3, 4/5, 6/7, 8/9, v.v.
- Một phần không đúng cách là một phần nhỏ có giá trị là hơn 1. Khi giá trị của tử số lớn hơn giá trị của mẫu số, sau đó phần được gọi là phân số không đúng. Ví dụ, 3/2, 5/4, 4/3. 8/3, v.v.
Phân số hỗn hợp
Khi một số là kết hợp của một số nguyên và một phân số thích hợp, thì nó được gọi là một phân số hỗn hợp . Ví dụ:
![]()
![]()
Xem thêm: