Nói chung, một hàm đa thức cũng được phát biểu như một biểu thức đa thức hoặc đa thức, được xác định theo bậc của nó. Các mức độ của bất kỳ đa thức là hiện quyền lực cao nhất trong đó. Trong bài viết này, bạn sẽ học hàm đa thức cùng với biểu thức và biểu diễn đồ họa của nó đối với đa thức bậc 0, một bậc, hai bậc và các đa thức bậc cao hơn.
Contents
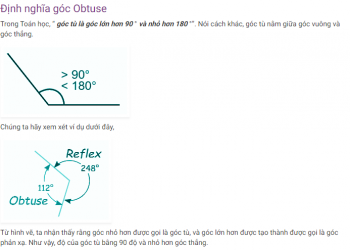
Định nghĩa hàm đa thức
Một hàm đa thức là một hàm có thể được biểu diễn dưới dạng một đa thức. Định nghĩa này có thể được rút ra từ định nghĩa của một phương trình đa thức . Một đa thức thường được biểu diễn dưới dạng P (x). Công suất cao nhất của biến P (x) được gọi là bậc của nó. Bậc của một hàm đa thức rất quan trọng vì nó cho chúng ta biết về hoạt động của hàm P (x) khi x trở nên rất lớn. Miền của một hàm đa thức là toàn bộ các số thực (R).
Nếu P (x) = a n x n + a n-1 x n-1 +. ……….… + A 2 x 2 + a 1 x + a 0 , thì với x ≫ 0 hoặc x ≪ 0, P (x) ≈ a n x n . Do đó, các hàm đa thức tiếp cận các hàm lũy thừa đối với các giá trị rất lớn của các biến của chúng.
Ví dụ về hàm đa thức
Một hàm đa thức chỉ có số nguyên dương là số mũ. Chúng tôi thậm chí có thể thực hiện các loại phép toán số học khác nhau cho các chức năng như cộng, trừ, nhân và chia.
Dưới đây là một số ví dụ về hàm đa thức:
- x 2 + 2x + 1
- 3x-7
- 7x 3 + x 2 -2
Cả ba biểu thức trên đều là đa thức vì tất cả các biến đều có số mũ nguyên dương. Nhưng những biểu hiện như;
- 5x -1 +1
- 4x 1/2 + 3x + 1
- (9x +1) ÷ (x)
không phải là đa thức, chúng ta không thể coi số mũ nguyên âm hoặc số mũ phân số hoặc phép chia ở đây.
Các loại hàm đa thức
Có nhiều loại hàm đa thức dựa trên bậc của đa thức. Các loại phổ biến nhất là:
- Hàm đa thức 0: P (x) = a = ax 0
- Hàm đa thức tuyến tính: P (x) = ax + b
- Hàm đa thức bậc hai: P (x) = ax 2 + bx + c
- Hàm đa thức khối: ax 3 + bx 2 + cx + d
- Hàm đa thức bậc ba: ax 4 + bx 3 + cx 2 + dx + e
Chi tiết của các hàm đa thức này cùng với đồ thị của chúng được giải thích dưới đây.
Đồ thị của các hàm đa thức
Đồ thị của P (x) phụ thuộc vào mức độ của nó. Đa thức có một biến có số mũ lớn nhất được gọi là bậc của đa thức.
Chúng ta hãy nhìn P (x) với các mức độ khác nhau.
Hàm đa thức số 0
Mức độ 0 (Chức năng không đổi)
- Dạng chuẩn: P (x) = a = ax 0 , trong đó a là hằng số.
- Đồ thị: Một đường nằm ngang chỉ ra rằng đầu ra của hàm là không đổi. Nó không phụ thuộc vào đầu vào.
Ví dụ: y = 4, (xem Hình 1)
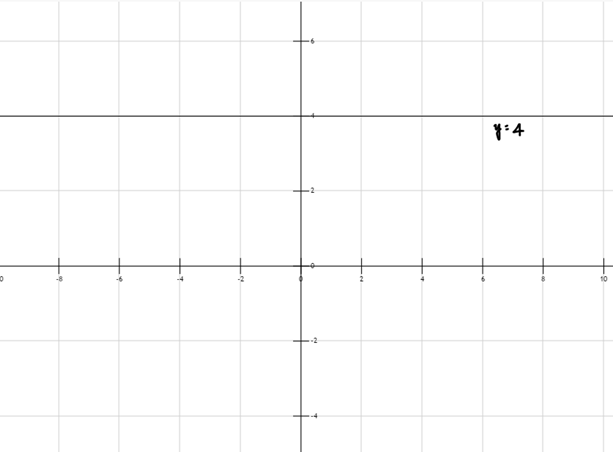

Hình 1: Đồ thị của hàm đa thức Zero
Hình 1: y = 4
Hàm đa thức tuyến tính
Mức độ 1, Hàm tuyến tính
- Dạng chuẩn: P (x) = ax + b, trong đó a và b là hằng số. Nó tạo thành một đường thẳng.
- Đồ thị: Hàm tuyến tính có một biến phụ thuộc và một biến độc lập tương ứng là x và y.
Trong công thức tiêu chuẩn cho bậc 1, a đại diện cho hệ số góc của một đường, hằng số b đại diện cho giao điểm y của một đường.
Ví dụ: y = 2x + 3 (xem Hình 2)
ở đây a = 2 và b = 3
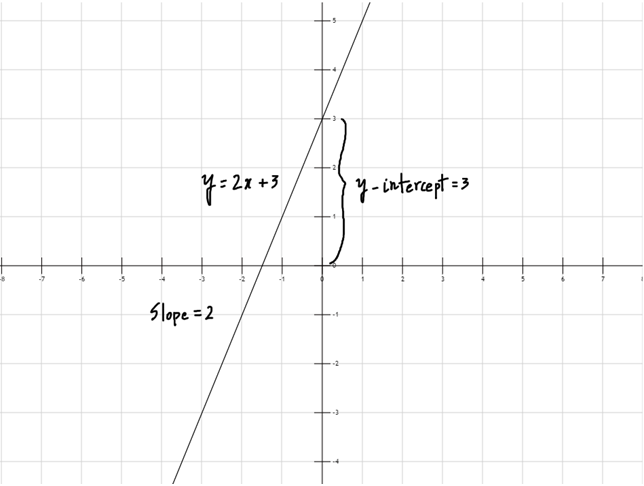

Hình 2: Đồ thị của các hàm đa thức tuyến tính
Hình 2: y = 2x + 3
Lưu ý: Tất cả các hàm hằng đều là hàm tuyến tính.
Hàm đa thức bậc hai
Mức độ 2, Hàm bậc hai
- Dạng chuẩn: P (x) = ax 2 + bx + c, trong đó a, b và c là hằng số.
- Đồ thị: Một parabol là một đường cong có một điểm cực trị được gọi là đỉnh. Parabol là một đường cong đối xứng qua gương trong đó một điểm bất kỳ nằm cách một điểm cố định một khoảng bằng nhau được gọi là Tiêu điểm.
Ở dạng chuẩn, hằng số ‘a’ thể hiện độ rộng của parabol. Khi ‘giảm’, độ rộng của parabol tăng lên. Có thể hình dung điều này bằng cách xem xét trường hợp biên khi a = 0, parabol trở thành đường thẳng. Hằng số c đại diện cho giao điểm y của parabol. Đỉnh của parabol được cho bởi
(h, k) = (-b / 2a, -D / 4a)
trong đó D là số phân biệt và bằng (b 2 -4ac).
Chú ý: Hình parabol hướng lên hay hướng xuống phụ thuộc vào tính chất của a.
- Nếu a> 0, parabol hướng lên trên.
- Nếu a <0, parabol hướng xuống dưới.
Ví dụ: y = x 2 + 2x-3 (hiển thị bằng màu đen)
y = -x 2 -2x + 3 (hiển thị bằng màu xanh lam)
(Xem Hình 3)
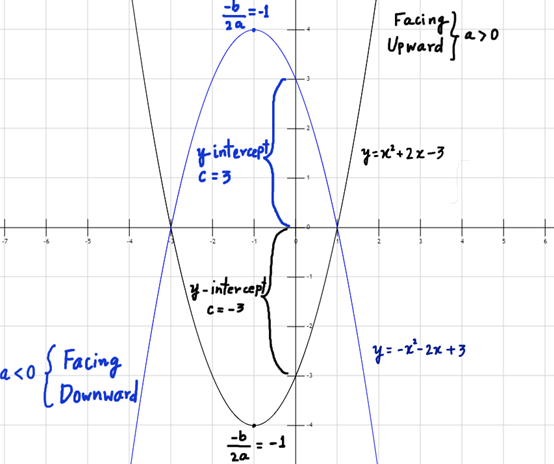

Hình 3: Các hàm đa thức bậc hai
Hình 3: y = x 2 + 2x-3 (đen) và y = x 2 -2x + 3 (xanh lam)
Đồ thị của các hàm đa thức bậc cao hơn
- Dạng chuẩn – P (x) = a n x n + a n-1 x n-1 +. ……….… + A 0 , trong đó a 0 , a 1 , ………, a n đều là hằng số.
- Đồ thị: Phụ thuộc vào tung độ, nếu P (x) có tung độ n thì bất kỳ đường thẳng nào cũng có thể cắt nó tại tối đa n điểm. Số hạng hằng trong biểu thức đa thức, tức là số 0 ở đây đại diện cho hệ thức y.
- Ví dụ: y = x 4 -2x 2 + x-2, bất kỳ đường thẳng nào cũng có thể cắt nó tại 4 điểm (xem hình 4)
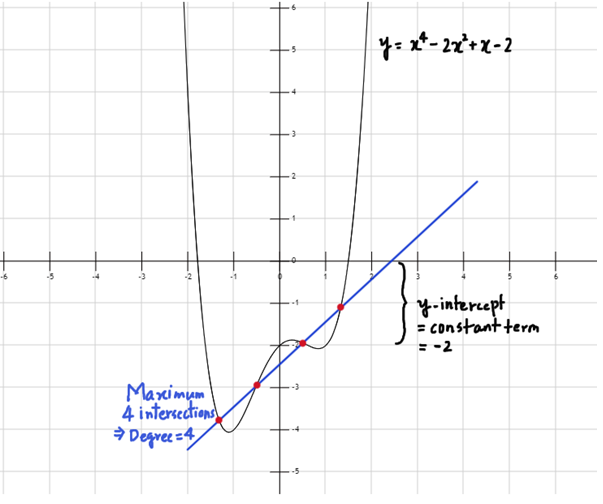

Hình 4: Đồ thị của các hàm đa thức bậc cao hơn
Câu hỏi về hàm đa thức
Q.1: Đa thức là gì?
Một đa thức được định nghĩa như là một biểu hình thành bởi tổng của quyền hạn của một hay nhiều biến nhân để hệ số. Ở dạng chuẩn, nó được biểu diễn dưới dạng:
a n x n + a n-1 x n-1 +. ……….… + A 2 x 2 + a 1 x + a 0
trong đó tất cả các lũy thừa là số nguyên không âm.
Và, a 0 , a 1 , ………, a n ∈ R
Đa thức được gọi là đơn biến hoặc đa biến nếu số biến tương ứng là một hoặc nhiều. Vì vậy, các biến của một đa thức chỉ có thể có lũy thừa dương.
Q.2: Bậc của Đa thức là gì?
Bậc của bất kỳ biểu thức đa thức nào là lũy thừa cao nhất của biến có trong biểu thức của nó. Đa thức hằng số (khác 0), đa thức tuyến tính, bậc hai, bậc ba và bậc bốn lần lượt là các đa thức bậc 0, 1, 2, 3 và 4. Hàm f (x) = 0 cũng là một đa thức, nhưng chúng ta nói rằng bậc của nó là ‘không xác định’.