| Nếu f và g là các hàm ngược, thì f (x) = y nếu và chỉ khi g (y) = x |
Trong lượng giác, hàm sin nghịch đảo được sử dụng để tìm số đo góc mà hàm sin tạo ra giá trị. Ví dụ, sin -1 (1) = sin -1 (sin 90) = 90 độ. Do đó, sin 90 độ bằng 1.
Định nghĩa
Một hàm chấp nhận các giá trị, thực hiện các hoạt động cụ thể trên các giá trị này và tạo ra một đầu ra. Hàm nghịch đảo đồng ý với kết quả, hoạt động và quay trở lại hàm ban đầu.
| Hàm nghịch đảo trả về giá trị ban đầu mà hàm đã cho đầu ra. |
Nếu bạn xét các hàm, f và g là nghịch biến, f (g (x)) = g (f (x)) = x. Một hàm bao gồm nghịch đảo của nó sẽ lấy giá trị ban đầu.
Ví dụ: f (x) = 2x + 5 = y
Khi đó, g (y) = (y-5) / 2 = x là nghịch đảo của f (x).
Ghi chú:
- Mối quan hệ, được phát triển khi biến độc lập được hoán đổi cho nhau với biến phụ thuộc vào một phương trình xác định và nghịch đảo này có thể là một hàm hoặc có thể không.
- Nếu nghịch đảo của một hàm là chính nó, thì nó được gọi là hàm ngược, ký hiệu là f -1 (x).
Đồ thị hàm ngược
Đồ thị nghịch biến của một hàm số phản ánh hai điều, một là hàm số và hai là nghịch biến của hàm số, trên đường thẳng y = x. Đường này trong đồ thị đi qua điểm gốc và có giá trị hệ số góc 1. Nó có thể được biểu diễn dưới dạng;
y = f -1 (x)
mà bằng;
x = f (y)
Mối quan hệ này tương tự như y = f (x), xác định đồ thị của f nhưng phần của x và y được đảo ngược ở đây. Vì vậy, nếu chúng ta phải vẽ đồ thị của f -1 , thì chúng ta phải chuyển vị trí của x và y theo các trục.
Làm thế nào để Tìm nghịch đảo của một hàm?
Nói chung, phương pháp tính nghịch đảo là hoán đổi tọa độ x và y. Nghịch đảo mới được tạo này là một quan hệ nhưng không nhất thiết là một hàm.
Hàm ban đầu phải là một hàm một đối một để đảm bảo rằng nghịch đảo của nó cũng sẽ là một hàm. Một hàm được cho là hàm 1-1 chỉ khi mỗi phần tử thứ hai tương ứng với giá trị đầu tiên (các giá trị của x và y chỉ được sử dụng một lần).
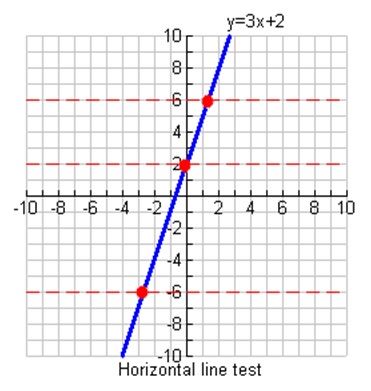

Bạn có thể áp dụng bài kiểm tra đường ngang để xác minh xem một hàm có phải là hàm một đối một hay không. Nếu một đường ngang cắt hàm ban đầu trong một vùng duy nhất thì hàm là một hàm một và nghịch đảo cũng là một hàm.
Các loại chức năng nghịch đảo
Có nhiều dạng hàm ngược khác nhau như hàm ngược của hàm lượng giác, hàm hữu tỉ, hàm hypebol và hàm log. Phần nghịch đảo của một số hàm phổ biến nhất được đưa ra dưới đây.
| Chức năng | Nghịch đảo của chức năng | Bình luận |
|---|---|---|
| + | – | |
| × | / | Không chia cho 0 |
| 1 / x | 1 / và | x và y không bằng 0 |
| x 2 | √y | x và y ≥ 0 |
| x n | y 1 / n | n không bằng 0 |
| e x | ln (y) | y> 0 |
| một x | log a (y) | y và a> 0 |
| Không có (x) | Không có -1 (và) | – π / 2 đến + π / 2 |
| Cos (x) | Cos -1 (y) | 0 đến π |
| Tân (x) | Tan -1 (và) | – π / 2 đến + π / 2 |
Hàm lượng giác ngược
Các hàm lượng giác nghịch đảo còn được gọi là hàm cung vì chúng tạo ra độ dài của cung, cần thiết để đạt được giá trị cụ thể đó. Có sáu hàm lượng giác nghịch đảo bao gồm arcsine (sin -1 ), arccosine (cos -1 ), arctangent (tan -1 ), arcsecant (sec -1 ), arccosecant (cosec -1 ) và arccotangent (cot -1 ) .
Hàm số hợp lý nghịch đảo
Một hàm hữu tỉ là một hàm có dạng f (x) = P (x) / Q (x) trong đó Q (x) ≠ 0. Để tìm nghịch đảo của một hàm hữu tỉ, hãy làm theo các bước sau. Dưới đây là một ví dụ có thể giúp bạn hiểu rõ hơn về khái niệm này.
- Bước 1: Thay f (x) = y
- Bước 2: Trao đổi x và y
- Bước 3: Giải y theo x
- Bước 4: Thay y bằng f -1 (x) ta được hàm số nghịch biến.
Hàm Hyperbolic Nghịch đảo
Cũng giống như các hàm lượng giác nghịch đảo, các hàm hyperbolic nghịch đảo là các nghịch đảo của các hàm hyperbolic. Chủ yếu tồn tại 6 hàm hypebol nghịch đảo bao gồm sinh -1 , cosh -1 , tanh -1 , csch -1 , coth -1 và sech -1 .
Hàm logarit nghịch đảo và hàm mũ nghịch đảo
Các hàm log tự nhiên là nghịch đảo của các hàm mũ. Kiểm tra ví dụ sau để hiểu chi tiết về hàm số mũ nghịch đảo và hàm số lôgarit. Ngoài ra, có thêm hiểu biết về cách giải quyết các câu hỏi tương tự và do đó, phát triển kỹ năng giải quyết vấn đề.
Tìm hàm số nghịch đảo bằng đại số
Đặt “y” cho “f (x)” và giải cho x:
| Chức năng: | f (x) | = | 2x + 3 |
| Đặt “y” cho “f (x)”: | Y | = | 2x + 3 |
| Trừ 3 cho cả hai bên: | y-3 | = | 2x |
| Chia cả hai bên cho 2: | (y-3) / 2 | = | x |
| Hoán đổi bên: | x | = | (y-3) / 2 |
| Giải pháp (đặt “f -1 (y)” cho “x”): | f -1 (y) | = | (y-3) / 2 |
Ví dụ về hàm ngược
Ví dụ 1:
Tìm nghịch biến của hàm f (x) = ln (x – 2)
Giải pháp:
Đầu tiên, thay f (x) bằng y
Vì vậy, y = ln (x – 2)
Thay vào phương trình theo cấp số nhân, x – 2 = e y
Bây giờ, giải quyết cho x,
x = 2 + e y
Bây giờ, thay x bằng y và do đó, f -1 (x) = y = 2 + e y
Ví dụ 2:
Giải: f (x) = 2x + 3, tại x = 4
Giải pháp:
Chúng ta có,
f (4) = 2 × 4 + 3
f (4) = 11
Bây giờ, chúng ta hãy áp dụng ngược lại trên 11.
f -1 (11) = (11 – 3) / 2
f -1 (11) = 4
Thật kỳ diệu, chúng tôi nhận được 4 một lần nữa.
Do đó, f -1 (f (4)) = 4
Vì vậy, khi chúng ta áp dụng hàm f và hàm f -1 đảo ngược của nó sẽ đưa lại giá trị ban đầu trở lại, tức là f -1 (f (x)) = x.
Ví dụ 3:
Tìm nghịch biến của hàm số f (x) = (3x + 2) / (x-1)
Giải pháp:
Đầu tiên, thay f (x) bằng y và hàm trở thành,
y = (3x + 2) / (x-1)
Bằng cách thay thế x bằng y, chúng ta nhận được,
x = (3y + 2) / (y-1)
Bây giờ, giải y theo x:
x (y – 1) = 3y + 2
=> xy – x = 3y +2
=> xy – 3y = 2 + x
=> y (x – 3) = 2 + x
=> y = (2 + x) / (x – 3)
Vì vậy, y = f -1 (x) = (x + 2) / (x-3)
Câu hỏi thường gặp – Câu hỏi thường gặp
Hàm nghịch đảo là gì?
Làm thế nào để tìm nghịch đảo của một hàm?
Cho f (x) = 2x + 3 = y
y = 2x + 3
x = (y-3) / 2 = f -1 (y)
Đây là nghịch đảo của f (x).
Hàm số nghịch biến và nghịch biến của hàm số có giống nhau không?
Ví dụ, f (x) = 2x = y
f -1 (y) = y / 2 = x, là nghịch đảo của f ( x).
Nhưng, 1 / f (x) = 1 / 2x = f (x) -1 là nghịch biến của hàm f (x).
Nghịch đảo của 1 / x là gì?
đó nghịch đảo của f (x) sẽ là f -1 (y).
f -1 (y) = 1 / x
Làm thế nào để giải quyết hàm lượng giác nghịch đảo?
Như chúng ta đã biết, sin 30 ° = ½.
Do đó, sin x = ½
x = sin -1 (½) = sin -1 (sin 30 °) = 30 °