Hàm sin hay hàm sin là một trong ba hàm cơ bản trong lượng giác, các hàm khác là hàm cosin và hàm tan. Sin x hoặc sin theta có thể được định nghĩa là tỷ số của cạnh đối diện của tam giác vuông với cạnh huyền của nó.
Các mặt của một tam giác là gì? Xem xong 5 phút hiểu luôn.
Contents
Định nghĩa hàm sin
Hàm sin có thể được định nghĩa là tỷ số giữa độ dài cạnh đối diện với cạnh huyền trong một tam giác vuông. Đối với bất kỳ tam giác nào, giả sử ABC, với một góc alpha, hàm sin sẽ là:


Sin α = Ngược lại / Hypotenuse
Công thức hàm sin
Từ sơ đồ trên, biết rằng Sin α = BC / AB.
Bây giờ, công thức sin có thể được viết dưới dạng:
Sin α = a / h
Bảng giá trị sin
| Độ sin | Giá trị |
| 0 ° của nó | 0 |
| Của nó 30 ° | 1/2 |
| Của nó 45 ° | 1 / √2 |
| Của nó 60 ° | √3 / 2 |
| Của nó 90 ° | 1 |
| 120 ° của nó | √3 / 2 |
| 150 ° của nó | 1/2 |
| 180 ° của nó | 0 |
| 270 ° của nó | -1 |
| 360 ° của nó | 0 |
Giá trị sin bổ sung
| Sine 1 độ là 0,84 | Sine 2 độ là 0,91 |
| Sine 5 độ là -0,96 | Sine 10 độ là -0,54 |
| Sine 20 độ là 0,91 | Sine 30 độ là -0,99 |
| Sine 40 độ là 0,75 | Sine 50 độ là -0,26 |
| Sine 70 độ là 0,77 | Sine 80 độ là -0,99 |
| Sine 100 độ là -0,50 | Sine 105 độ là -0,97 |
| Sine 210 độ là 0,47 | Sine 240 độ là 0,95 |
| Sine 330 độ là -0,13 | Sine 350 độ là 0,95 |
Thuộc tính của sin theo góc phần tư
Hàm sin có giá trị dương hoặc âm tùy thuộc vào các góc phần tư. Trong bảng trên, ta thấy rằng sin 270 là âm trong khi sin 90 là dương. Đối với hàm sin, giá trị phụ thuộc vào các góc phần tư và dương đối với góc phần tư thứ nhất và thứ hai trong khi nó âm đối với các giá trị ở góc phần tư thứ ba và thứ tư.
Bốn góc phần tư trong biểu đồ Lượng giác:


| Phạm vi mức độ | Góc phần tư | Dấu hiệu hàm sin | Phạm vi giá trị sin |
| 0 đến 90 độ | Góc phần tư thứ nhất | + (Tích cực) | 0 <sin (x) <1 |
| 90 đến 180 độ | Góc phần tư thứ hai | + (Tích cực) | 0 <sin (x) <1 |
| 180 đến 270 độ | Góc phần tư thứ 3 | – (Tiêu cực) | -1 <sin (x) <0 |
| 270 đến 360 độ | Góc phần tư thứ 4 | – (Tiêu cực) | -1 <sin (x) <0 |
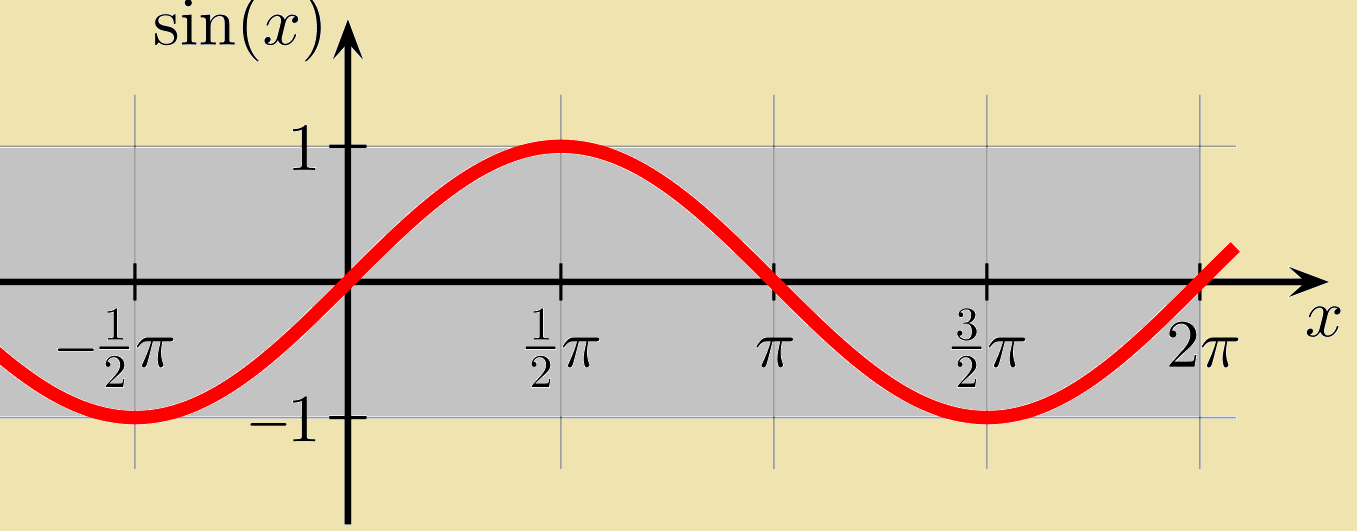
Đồ thị hàm sin
Biểu đồ sin trông giống như hình bên dưới. Các đồ thị hình sin hoặc đồ thị hình sin là một biểu đồ lên xuống và lặp đi lặp lại mỗi 360 độ tức là tại 2π. Trong sơ đồ dưới đây, có thể thấy rằng từ 0, đồ thị sin tăng lên đến +1 và sau đó giảm trở lại cho đến -1 từ nơi nó tăng trở lại.

Inverse Sine
Hàm nghịch đảo sin được sử dụng để đo góc của một tam giác vuông từ các tỉ số đã cho. Nghịch đảo của sin được ký hiệu là arcsine, asin hoặc sin -1 .
Giả sử một tam giác vuông được lấy với cạnh 1, 2 và √3 . Bây giờ, để tính góc a, hàm sin có thể được sử dụng như-


Bây giờ, sin (a) = đối diện / cạnh huyền tức là ½.
Góc A bây giờ có thể được tính bằng cách sử dụng hàm arcsine.
sin −1 (½) = a
Điều này sẽ cho giá trị của góc “a” là 30 °
Nhận dạng sin
Một số đặc điểm nhận dạng hình sin phổ biến là:
- sin (θ) = cos (π / 2 – θ) = 1 / cosec (θ)
- arcsin (sin θ) = θ, với −π / 2 ≤ θ ≤ π / 2
- cos 2 (θ) + sin 2 (θ) = 1
- Sin (2x) = 2sin (x) cos (x)
- Cos (2x) = cos 2 (x) – sin 2 (x)
Có nhiều đặc điểm nhận dạng sin khác. Giá trị của các hàm lượng giác khác theo sin cũng được đưa ra dưới đây, cực kỳ hữu ích để giải các dạng câu hỏi khác nhau.
Các hàm lượng giác khác trong thuật ngữ của sin
| Hàm lượng giác | Được đại diện là Sine |
| cos θ | ±1–s tôin2( i )———-√ |
| tan θ | ±s tôi n ( θ )1–s tôin2( i )√ |
| cũi θ | ±1–s tôin2( i )√s tôi n ( θ ) |
| giây θ | ±11–s tôin2( i )√ |
không tính toán
Đối với hàm sin f (x) = sin (x) ,, đạo hàm và tích phân sẽ được cho là:
- Đạo hàm của sin (x), f ′ (x) = cos (x)
- Tích phân của sin (x), ∫f (x) dx = −cos (x) + C (trong đó C là hằng số của tích phân)
Định luật Sines trong lượng giác
Theo luật sin trong lượng giác, một quan hệ được thiết lập giữa các cạnh a, b, c và các góc đối diện với các cạnh đó A, B và C để tạo ra một tam giác trọng tài. Mối quan hệ như sau.


Trong sơ đồ trên, A, B, C là các góc trong khi a, b, c là độ dài các cạnh. Bây giờ, theo luật sin,
aStôi nA=bStôi nB=cStôi nC=d(Ở đây, d là đường kính của đường tròn ngoại tiếp tam giác).
Hãy xem bài viết luật sin để biết thêm về nó và biết cách chứng minh luật sin, các ví dụ và các chi tiết khác.
Cũng kiểm tra: Định luật Cosine
Sine Worksheet (Câu hỏi)
- Sin của 60 là gì?
- Tội lỗi 270 là gì?
- Sin 120 độ là gì?
- Đánh giá tội lỗi 360 độ.
- Suy ra giá trị của sin 60 về mặt hình học.
- Tìm giá trị của sin 30 về mặt hình học và chứng minh sin 30 về mặt hình học.
- Tại sao sin 90 là 1?
- Sin chia cho cosine là gì?
- Một chiếc máy bay đang bay ở độ cao 6000 feet so với mặt đất. Máy bay phải hạ xuống ở góc nào để hạ cánh xuống đường băng mục tiêu nếu nó cách đường băng 10.000 feet?
- Trong tam giác ABC, AC là 14 cm, CB là 10 cm và góc CBA là 63 độ. Tính góc CAB và độ dài AB.
- Cho tam giác ABC, sin (ABC) là 0,6 và độ dài BC là 12 cm. Tìm độ dài AC (cạnh huyền).
- Một sợi dây dài 55 m được nối với một điểm trên mặt đất từ đỉnh cột. Nếu sợi dây tạo với mặt đất một góc 60 độ, hãy tính chiều cao của cột.
Xem thêm: