Hàm số mũ là gì? Xem xong hiểu luôn.

• Định nghĩa
• Công thức
• Đồ thị
• Phát sinh
• Loạt
• Tính chất
• Quy tắc
• Các ví dụ
• Vấn đề

Hàm số mũ là gì?

Hàm mũ là một hàm toán học ở dạng f (x) = a ^x , trong đó “x” là một biến và “a” là một hằng số được gọi là cơ sở của hàm và nó phải lớn hơn 0. Thông dụng nhất Cơ số hàm mũ được sử dụng là số siêu việt e, xấp xỉ bằng 2,71828.

Công thức hàm mũ

Một hàm mũ được xác định bởi công thức f (x) = a ^x , trong đó biến đầu vào x xảy ra dưới dạng số mũ. Đường cong hàm mũ phụ thuộc vào hàm số mũ và nó phụ thuộc vào giá trị của x.

Hàm mũ là một hàm toán học quan trọng có dạng

f (x) = a ^x

Trường hợp a> 0 và a không bằng 1.

x là số thực bất kỳ.

Nếu biến là âm, hàm không xác định với -1 <x <1.

Đây,

“X” là một biến

“A” là một hằng số, là cơ sở của hàm.

Một đường cong hàm mũ lớn lên hoặc suy giảm phụ thuộc vào hàm số mũ. Bất kỳ số lượng nào tăng hoặc giảm theo một phần trăm cố định trong các khoảng thời gian đều đặn sẽ có mức tăng trưởng theo cấp số nhân hoặc giảm dần theo cấp số nhân.

Tăng trưởng theo cấp số nhân

Trong Tăng trưởng theo cấp số nhân, số lượng lúc đầu tăng rất chậm, sau đó tăng nhanh. Tỷ lệ thay đổi tăng dần theo thời gian. Tốc độ tăng trưởng trở nên nhanh hơn khi thời gian trôi qua. Sự tăng trưởng nhanh chóng có nghĩa là “sự gia tăng theo cấp số nhân”. Công thức để xác định tăng trưởng theo cấp số nhân là:

y = a (1+ r) ^x

Trong đó r là phần trăm tăng trưởng.

Giảm dần theo cấp số nhân

Trong Giảm dần theo cấp số nhân, số lượng giảm rất nhanh lúc đầu, sau đó từ từ. Tỷ lệ thay đổi giảm dần theo thời gian. Tốc độ thay đổi trở nên chậm hơn khi thời gian trôi qua. Sự tăng trưởng nhanh chóng có nghĩa là “giảm theo cấp số nhân”. Công thức để xác định tăng trưởng theo cấp số nhân là:

y = a (1- r) ^x

Trong đó r là phần trăm phân rã.

Đồ thị hàm số mũ

Hình sau biểu diễn đồ thị số mũ của x. Có thể thấy rằng khi số mũ tăng lên, các đường cong càng dốc và tốc độ tăng tương ứng. Do đó, với x> 1, giá trị của y = f _n (x) tăng khi các giá trị tăng của (n).

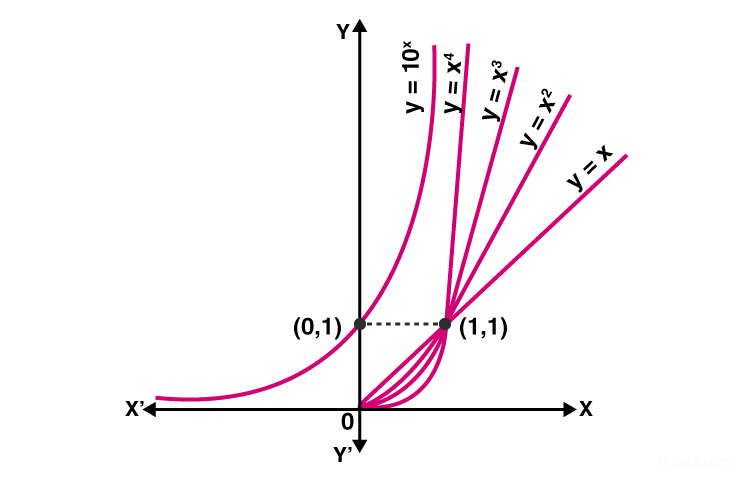
Từ những điều trên có thể thấy rằng bản chất của hàm đa thức là phụ thuộc vào bậc của nó. Mức độ của bất kỳ hàm đa thức nào càng cao thì mức tăng trưởng của nó càng cao. Hàm phát triển nhanh hơn hàm đa thức là y = f (x) = a ^x , trong đó a> 1. Do đó, với bất kỳ số nguyên dương n nào, hàm f (x) được cho là phát triển nhanh hơn hàm f _n (x).

Do đó, hàm mũ có cơ số lớn hơn 1, tức là a> 1 được xác định là y = f (x) = a ^x . Miền của hàm số mũ sẽ là tập toàn bộ các số thực R và phạm vi được cho là tập hợp tất cả các số thực dương.

Cần lưu ý rằng hàm số lũy thừa đang tăng và điểm (0, 1) luôn nằm trên đồ thị của hàm số lũy thừa. Ngoài ra, nó rất gần bằng 0 nếu giá trị của x chủ yếu là số âm.

Hàm số mũ có cơ số 10 được gọi là một hàm số mũ phổ biến. Hãy xem xét loạt bài sau:

Giá trị của chuỗi này nằm giữa 2 & 3. Nó được đại diện bởi e. Giữ e là cơ sở của hàm, chúng ta nhận được y = e ^x , đây là một hàm rất quan trọng trong toán học được gọi là hàm mũ tự nhiên.

Với a> 1, logarit của b đối với cơ số a là x nếu a ^x = b. Như vậy, log _a b = x nếu a ^x = b. Hàm này được gọi là hàm logarit.

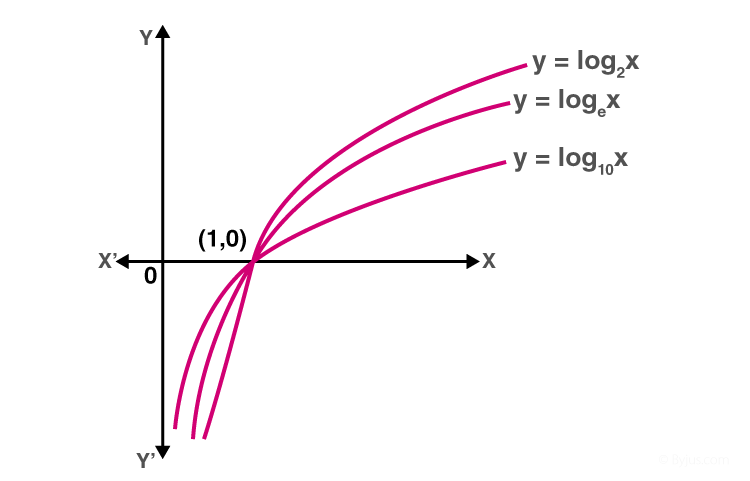
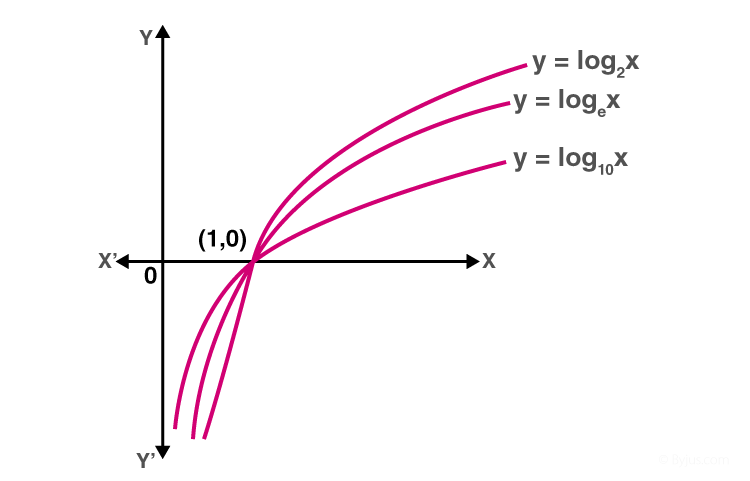
Đối với cơ số a = 10, hàm này được gọi là logarit chung và đối với cơ số a = e, nó được gọi là logarit tự nhiên ký hiệu là ln x. Sau đây là một số quan sát quan trọng liên quan đến các hàm số lôgarit có cơ số a> 1.

• Miền của hàm log chỉ bao gồm các số thực dương , vì chúng ta không thể giải thích ý nghĩa của hàm log cho các giá trị âm.
• Đối với hàm log, mặc dù miền chỉ là tập các số thực dương, nhưng phạm vi là tập tất cả các giá trị thực, tức là R
• Khi chúng ta vẽ đồ thị của các hàm log và di chuyển từ trái sang phải, các hàm thể hiện hành vi ngày càng tăng.
• Đồ thị của hàm log không bao giờ cắt trục x hoặc trục y, mặc dù nó có xu hướng về phía chúng.

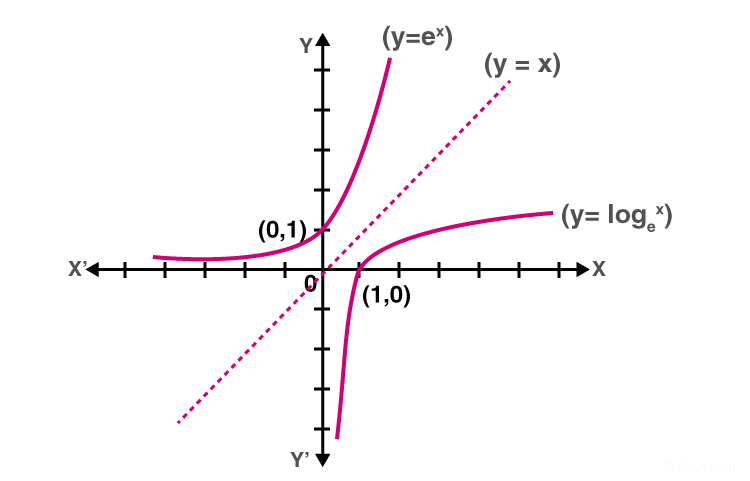
• Log _a p = α, log _b p = β và log _b a = µ, thì a ^α = p, b ^β = p và b ^µ = a
• Log _b pq = Log _b p + Log _b q
• Nhật ký _b p ^y = ylog _b p
• Log _b (p / q) = log _b p – log _b q

Đạo hàm hàm mũ

Bây giờ chúng ta hãy tập trung vào đạo hàm của hàm số mũ.

Đạo hàm của e ^x  đối với x là e ^x , tức là d (e ^x ) / dx = e ^x

Cần lưu ý rằng hàm mũ f (x) = e ^x   có một tính chất đặc biệt. Có nghĩa là đạo hàm của hàm là chính hàm.

(tức là) f ‘(x) = e ^x  = f (x)

Chuỗi số mũ

Thuộc tính hàm mũ

Đồ thị hàm số lũy thừa biểu diễn các tính chất của hàm số lũy thừa.

Chúng ta hãy xem xét hàm mũ, y = 2 ^x

Đồ thị của hàm số y = 2 ^x như hình bên dưới. Thứ nhất, tính chất của đồ thị hàm số mũ khi cơ số lớn hơn 1.

Đồ thị hàm số mũ cho y = 2 ^x

Đồ thị đi qua điểm (0,1).

• Miền là tất cả các số thực
• Phạm vi là y> 0
• Biểu đồ đang tăng
• Đồ thị tiệm cận với trục x khi x tiến tới âm vô cùng
• Đồ thị tăng mà không bị ràng buộc khi x tiến tới dương vô cùng
• Đồ thị liên tục
• Đồ thị mượt mà

Đồ thị hàm số mũ y = 2 ^-x 

Đồ thị của hàm số y = 2 ^-x như hình trên. Các tính chất của hàm số mũ và đồ thị của nó khi cơ số từ 0 đến 1 đã cho.

• Đường thẳng đi qua điểm (0,1)
• Miền bao gồm tất cả các số thực
• Phạm vi của y> 0
• Nó tạo thành một đồ thị giảm dần
• Đường trong biểu đồ trên tiệm cận với trục x khi x tiến tới dương vô cùng
• Dòng tăng mà không bị ràng buộc khi x tiến tới âm vô cùng
• Nó là một đồ thị liên tục
• Nó tạo thành một đồ thị mượt mà

Quy tắc hàm mũ

Một số quy tắc cấp số nhân quan trọng được đưa ra dưới đây:

Nếu a> 0 và b> 0, điều sau đúng với tất cả các số thực x và y:

• • a ^x  a ^y = a ^{x + y}
  • a ^x / a ^y = a ^x-y
  • (a ^x ) ^y = a ^xy
  • a ^x b ^x = (ab) ^x
  • (a / b) ^x = a ^x / b ^x
  • a ⁰ = 1
  • a ^-x = 1 / a ^x

Ví dụ về hàm số mũ

Các ví dụ về hàm số mũ là:

• f (x) = 2 ^x
• f (x) = 1/2 ^x  = 2 ^-x
• f (x) = 2 ^{x + 3}
• f (x) = 0,5 ^x

Giải quyết vấn đề

Câu hỏi:

Đơn giản hóa phương trình mũ 2 ^x -2 ^{x + 1}

Giải pháp:

Cho phương trình mũ: 2 ^x -2 ^{x + 1}

Bằng cách sử dụng thuộc tính: a ^x  a ^y  = a ^{x + y}

Do đó, 2 ^{x + 1}  có thể được viết thành 2 ^x . 2

 Do đó, phương trình đã cho được viết thành:

2 ^x -2 ^{x + 1}  = 2 ^x -2 ^x . 2

Bây giờ, thừa số hạng 2 ^x

2 ^x -2 ^{x + 1}  = 2 ^x -2 ^x . 2 = 2 ^x (1-2)

2 ^x -2 ^{x + 1}  = 2 ^x (-1)

2 ^x -2 ^{x + 1}  = – 2 ^x

Do đó, đơn giản của phương trình lũy thừa đã cho 2 ^x -2 ^{x + 1} là – 2 ^x .

Xanthogranuloma vị thành niên là gì? Những nguyên nhân, triệu chứng

Ung thư niệu đạo nam giới là gì? Những thông tin liên quan