Hàm tuyến tính là gì?
Một hàm tuyến tính là một hàm tạo thành một đường thẳng trong một đồ thị. Nói chung, nó là một hàm đa thức mà bậc của nó lớn nhất là 1 hoặc 0. Mặc dù các hàm tuyến tính cũng được biểu diễn dưới dạng giải tích cũng như đại số tuyến tính . Sự khác biệt duy nhất là ký hiệu chức năng. Biết một cặp có thứ tự được viết bằng ký hiệu hàm cũng cần thiết. f (a) được gọi là một hàm, trong đó a là một biến độc lập, trong đó hàm phụ thuộc. Đồ thị hàm tuyến tính có một đường thẳng mà biểu thức hoặc công thức được cho bởi;
y = f (x) = px + q
Nó có một biến độc lập và một biến phụ thuộc. Biến độc lập là x và biến phụ thuộc là y. P là số hạng không đổi hoặc hàm y và cũng là giá trị của biến phụ thuộc. Khi x = 0, q là hệ số của biến độc lập được gọi là độ dốc cho tốc độ thay đổi của biến phụ thuộc.
Hàm phi tuyến là gì?
Một hàm không tuyến tính được gọi là hàm phi tuyến. Nói cách khác, một hàm không tạo thành một đường thẳng trong một đồ thị. Ví dụ của các hàm đó là hàm số mũ, hàm số parabol, hàm số nghịch biến, hàm số bậc hai, … Tất cả các hàm số này không thỏa mãn phương trình tuyến tính y = mx + c. Biểu thức cho tất cả các hàm này là khác nhau.
Đồ thị hàm tuyến tính
Vẽ đồ thị của một phương trình tuyến tính bao gồm ba bước đơn giản:
- Trước hết, chúng ta cần tìm hai điểm thỏa mãn phương trình, y = px + q.
- Bây giờ vẽ các điểm này trong đồ thị hoặc mặt phẳng XY.
- Nối hai điểm trong mặt phẳng với sự trợ giúp của một đường thẳng.


Bảng hàm tuyến tính
Xem bảng dưới đây trong đó ký hiệu của cặp có thứ tự được tổng quát ở dạng chuẩn và dạng hàm.
| Một cặp được đặt hàng bình thường | Một cặp có thứ tự ký hiệu hàm |
| (a, b) = (2,5) | tọa độ f (a) = y, a = 2 và y = 5, f (2) = 5 |
Sử dụng bảng, chúng ta có thể xác minh hàm tuyến tính, bằng cách kiểm tra các giá trị của x và y. Đối với hàm tuyến tính, tốc độ thay đổi của y đối với biến x không đổi. Khi đó, tốc độ thay đổi được gọi là độ dốc.
Chúng ta hãy xem xét bảng đã cho,
| x | Y |
| 0 | 3 |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
| 4 | 7 |
Lập bảng, quan sát thấy rằng, tỷ lệ thay đổi giữa x và y là 3. Điều này có thể được viết bằng cách sử dụng hàm tuyến tính y = x + 3.
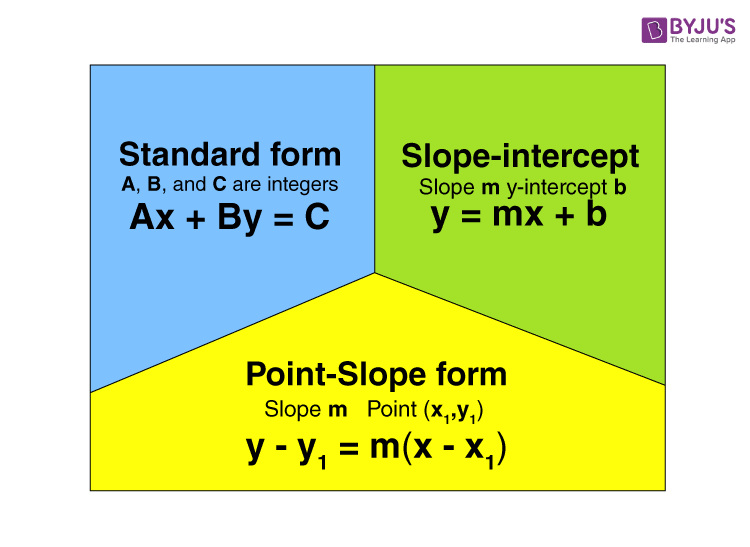
Công thức hàm tuyến tính
Biểu thức của hàm tuyến tính là công thức để vẽ đồ thị một đường thẳng. Biểu thức của phương trình tuyến tính là;
y = mx + c
với m là hệ số góc, c là giao điểm và (x, y) là tọa độ. Công thức này còn được gọi là công thức hệ số góc .
Trong khi xét về mặt chức năng, chúng ta có thể biểu thị biểu thức trên là;
f (x) = ax + b, trong đó x là biến độc lập.

Đặc điểm của hàm tuyến tính
Hãy chuyển sang xem làm thế nào chúng ta có thể sử dụng ký hiệu hàm để vẽ đồ thị 2 điểm trên lưới.
- Quan hệ : Là một nhóm các cặp có thứ tự.
- Biến : Một ký hiệu thể hiện một đại lượng trong một biểu thức toán học.
- Hàm tuyến tính : Nếu mỗi số hạng là một hằng số hoặc Nó là tích của một hằng số và cũng là (lũy thừa bậc nhất của) một biến duy nhất, thì nó được gọi là một phương trình đại số.
- Chức năng : Một chức năng là một quan hệ giữa một tập hợp các đầu vào và một tập hợp các đầu ra cho phép. Nó có một thuộc tính mà mỗi đầu vào liên quan đến chính xác một đầu ra.
- Độ dốc : Tốc độ tại đó một hàm lệch khỏi tham chiếu
- Hướng : Tăng, giảm, ngang hoặc dọc.
Ví dụ về hàm tuyến tính
Vẽ đồ thị của hàm tuyến tính cần học phương trình tuyến tính hai biến.
Ví dụ 1 :
Hãy vẽ đồ thị cho hàm số sau:
F (2) = -4 và f (5) = -3
Giải pháp:
- Hãy viết lại nó thành các cặp có thứ tự (hai trong số chúng).
- f (2) = -4 và f (5) = -3
(2, -4) (5, -3)
Làm thế nào để đánh giá hệ số góc của một hàm tuyến tính?
Hãy tìm hiểu nó với một ví dụ:
Ví dụ 2 :
Tìm hệ số góc của đồ thị cho hàm số sau.
f (3) = -1 và f (-8) = -6
Giải pháp:
Hãy viết lại nó thành các cặp có thứ tự
f (3) = -1 và f (8) = -6
(3, -1) (8, -6)
chúng ta sẽ sử dụng công thức độ dốc để đánh giá độ dốc
(3, -1) (8, -6)
(x 1 , y 1 ) (x 2 , y 2 )
Công thức độ dốc, m = Y2–Y1x2–x1 – 6 – ( – 1 )8 – ( – 3 )=– 55
m = 1 là hệ số góc của hàm này.
Ví dụ 3:
Tìm phương trình của hàm tuyến tính đã cho f (2) = 5 và f (6) = 3.
Giải pháp : Hãy viết nó thành một cặp có thứ tự
f (2) = 5 f (6) = 3
(2, 5) (6, 3)
Tìm hệ số góc.
(2, 5) (6, 3)
Y2–Y1x2–x1=3 – 56 – 2=– 24=– 12Độ dốc = -1/2
Trong phương trình, thay thế hệ số góc và hệ số y, viết một phương trình như sau: y = mx + c
5 = – (½) (2) + b
5 = -1 + b
b = 5 + 1
b = 6, là giao điểm y.
y = mx + b
y = – (½) (x) + 6
Trong hàm Ký hiệu: f (x) = – (½) (x) + 6
Xem thêm: