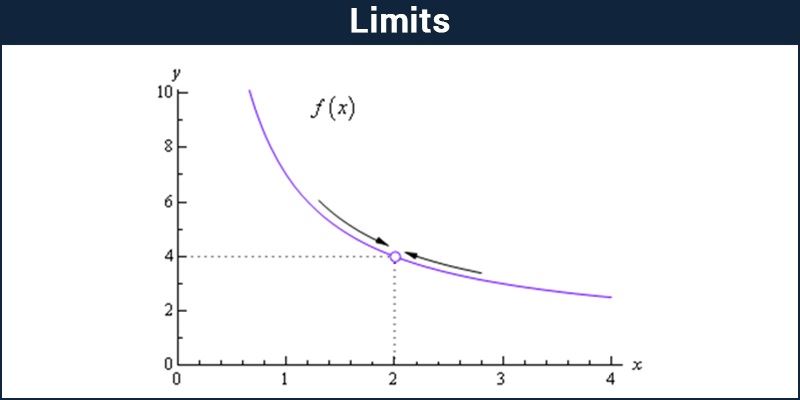

Định nghĩa giới hạn
Chúng ta hãy xem xét một hàm có giá trị thực “f” và số thực “c”, giới hạn thường được xác định là
limx → cf( x ) = L
Nó được đọc là “giới hạn của f của x, khi x tiến tới c bằng L”. “Lim” cho thấy giới hạn và thực tế là hàm f (x) tiến tới giới hạn L khi x tiến tới c được mô tả bằng mũi tên bên phải.
Thuộc tính của giới hạn
Sau đây là danh sách các thuộc tính của giới hạn.
Chúng tôi cho rằng limx → af( x ) và limx → ag( x )tồn tại và c là một hằng số. Sau đó,
- limx → a[ c . f( x ) ] =climx → af( x )
Bạn có thể nhân một hằng số nhân với một giới hạn.
- limx → a[ f( x ) ± g( x ) ] =limx → af( x ) ±limx → ag( x )
Để xem xét giới hạn của một tổng chênh lệch, hãy chọn từng giới hạn và đặt chúng lại với dấu tương ứng. Thực tế này hoạt động bất kể số lượng hàm mà chúng tôi đã phân tách bằng “+” hoặc “-”.
- limx → a[ f( x ) . g( x ) ] =limx → af( x ) .limx → ag( x )
Xem xét các giới hạn của các sản phẩm tương tự như các giới hạn của tổng hoặc sự khác biệt. Chỉ cần chọn giới hạn của các mảnh và đặt lại, và điều này không chỉ giới hạn ở hai chức năng.
- limx → a[f( x )g( x )] =limx → af( x )limx → ag( x ),
cung cấp limx → ag( x ) ≠ 0
Như bạn thấy, chúng ta chỉ cần bận tâm nếu giới hạn của mẫu số bằng 0 khi vận hành giới hạn thương số. Nếu nó bằng 0, nó sẽ có lỗi chia cho 0.
- limx → ac = c
Giới hạn của một hằng số chỉ là một hằng số. Bạn có thể dễ dàng hiểu nó bằng cách vẽ đồ thị của hàm số f (x) = c.
- limx → ax n = a n
Đọc: Các thuộc tính của Tích phân xác định
Ví dụ về giới hạn
Ví dụ 1:
Để tính toán limx → – 4( 5x2+ 8 x – 3 )
Giải pháp:
Đầu tiên, sử dụng thuộc tính 2 để chia giới hạn thành ba giới hạn riêng biệt. Sau đó, sử dụng thuộc tính 1 để đưa các hằng số ra khỏi hai hằng số đầu tiên. Điều này mang lại,
limx → – 4( 5x2+ 8 x – 3 ) =limx → – 4( 5x2) +limx → – 4( 8 x ) –limx → – 4( 3 )
= 5 ( – 4)2+ 8 ( – 4 ) – 3
= 80 – 32 – 3 = 45
Ví dụ 2:
Để tính toánlimx → 6[( x – 3 ) ( x – 2 )x – 4]
Giải pháp:
Được limx → 6[( x – 3 ) ( x – 2 )x – 4]
= [limx → 6( x – 3 )limx → 6( x – 2 )limx → 6( x – 4 )]
= [( 6 – 3 ) ( 6 – 2 )( 6 – 4 )]
= [( 3 ) ( 4 )( 2 )] =6
Ví dụ 3:
Tính toán limx → 3(x2– 9 )x – 3
Giải pháp: Đưa ralimx → 3(x2– 9 )x – 3
Cần lưu ý rằng, khi thay thế trực tiếp giá trị 3 vào funciton, nemerator cũng như mẫu số sẽ trở thành 0 và chúng ta biết giá trị 00, không tồn tại.
Sử dụng thuộc tính của hình vuông, chúng ta có:
limx → 3( x – 3 ) ( x + 3 )x – 3=limx → 3( x + 3 )
= 6
Xem thêm: