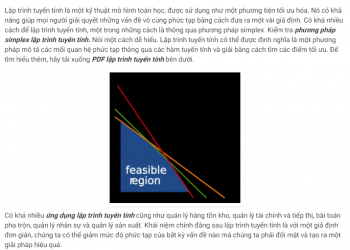
Dạng vectơ
Chúng ta hãy xem xét một điểm A có vectơ vị trí cho bởi ȃ và một mặt phẳng P, cho bởi phương trình,![]()
![]()


Ở đây, N là pháp tuyến đối với mặt phẳng P đang xét. Bây giờ, gọi O là gốc của hệ tọa độ và P ‘một mặt phẳng khác song song với mặt phẳng thứ nhất, được lấy sao cho nó đi qua điểm A. Ở đây, N’ là pháp tuyến của mặt phẳng thứ hai. Phương trình của mặt phẳng thứ hai P ‘được cho bởi,![]()
![]()
Hoặc là,

Ta thấy rằng ON cho khoảng cách của mặt phẳng P so với gốc tọa độ và ON ‘là khoảng cách của mặt phẳng P’ từ gốc tọa độ. Do đó, khoảng cách giữa hai mặt phẳng được cho là,![]()
![]()
Điều này cũng cho biết khoảng cách vuông góc của điểm A trên mặt phẳng P ‘từ mặt phẳng P.
Do đó, chúng tôi kết luận rằng, đối với một mặt phẳng được cho bởi phương trình
![]()
![]()
và một điểm A, với vectơ vị trí cho bởi, khoảng cách vuông góc của điểm đó từ mặt phẳng đã cho là

Để tính độ dài của mặt phẳng từ điểm gốc, chúng ta thay vectơ vị trí bằng 0, và do đó nó trở thành

Hình thức Descartes
Chúng ta hãy xem xét một mặt phẳng được cho bởi phương trình Descartes,
Ax + By + Cz = D
Và một điểm có vectơ vị trí là ȃ và tọa độ Descartes là,
![]()
![]()
Chúng ta có thể viết vectơ vị trí là:![]()
![]()
Để tìm khoảng cách của điểm A so với mặt phẳng bằng công thức đã cho ở dạng vectơ, trong phần trước, chúng ta tìm vectơ pháp tuyến đối với mặt phẳng, được cho là,![]()
![]()
Sử dụng công thức, khoảng cách vuông góc của điểm A từ mặt phẳng đã cho là,





Phương trình này cho chúng ta khoảng cách vuông góc của một điểm từ một mặt phẳng, sử dụng phương pháp Descartes.
Xem thêm: