Kiểm tra tích phân cho sự hội tụ
Phép thử tích phân cho sự hội tụ là một phương pháp được sử dụng để kiểm tra chuỗi vô hạn các số hạng không âm về sự hội tụ. Nó còn được gọi là Thử nghiệm Maclaurin-Cauchy.
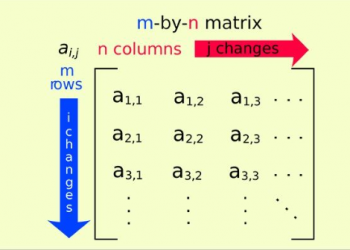
Gọi N là một số tự nhiên (số không âm) và nó là một hàm giảm đơn điệu, thì hàm được định nghĩa là
f: [N, ∞] → ℝ
Sau đó, loạt ∑∞m = Nf( m ) là hội tụ nếu và chỉ khi tích phân ∫∞Nf( t ) dt là hữu hạn.
Điều kiện để kiểm tra tích phân
Phép thử so sánh tích phân chủ yếu dành cho các số hạng tích phân. Nếu ta có hai hàm số f (x) và g (x) sao cho g (x) ≥ f (x) trên khoảng [c, ∞] đã cho, thì nó phải có các điều kiện sau.
- Nếu thuật ngữ ∫∞cg( x ) dx hội tụ, thì thuật ngữ này cũng vậy ∫∞cf( x ) dx.
- Nếu thuật ngữ ∫∞cf( x ) dx phân kỳ, thì thuật ngữ cũng vậy ∫∞cg( x ) dx.
Bằng chứng kiểm tra tích phân
Phép thử tích phân bằng chứng phụ thuộc vào phép thử so sánh. Chúng ta biết rằng,
∫∞Nf( t ) dt không là gì ngoài tổng hợp của chuỗi ∑∞m = N∫m + 1mf( t ) dtVì “f” là hàm giảm đơn điệu, nên
f (t) ≤ f (m) với mọi “t” trong [m, ∞]
Đối với m> N, ∫m + 1mf( t ) dt ≤ ∫m + 1mf( m ) dt = f (m)
Nó có nghĩa là ∫m + 1mf( t ) dt ≤ f (m)
Vì cả hai đại lượng đều không âm nên sử dụng phép thử so sánh.
Nếu ∑∞m = Nf( m ) hội tụ, sau đó ∑∞m = N∫m + 1mf( t ) dt = ∫∞Nf( t ) dt cũng hội tụ.
Đó là, nó là hữu hạn.
Vậy là chúng ta đã thực hiện xong một bước của chứng minh.
Bây giờ một lần nữa lấy f là hàm giảm đơn điệu, chúng ta nhận được
f (m) ≤ f (t) với mọi “x” trong [M, m]
Vì vậy, f (m) = ∫mm – 1f( t ) dt ≤ ∫mm – 1f( t ) dt
Từ định lý so sánh, chúng ta nhận được
Nếu ∑∞m = N∫mm – 1f( t ) dt = f( N) +∫∞Nf( t ) dt hội tụ, sau đó chúng ta có thể nói rằng ∑∞m = Nf( m ) cũng hội tụ, điều này chứng minh phần khác của định lý.
Ví dụ kiểm tra tích phân với giải pháp
Câu hỏi:
Kiểm tra sự hội tụ của ∑10n = 1n
Giải pháp:
Được: ∑10n = 1n
Chúng ta có thể định nghĩa nó là
f: [N, ∞] → ℝ
f: [1,10] → ℝ bởi f (x) = x = n
Vì vậy, chúng ta có thể viết nó là
∫101f( x ) dx =∫101x dx= [x22]101
= (10 2 /2) – (1 2 /2)
= 50 – (½)
= 99/2 = 49,5
Do đó, bằng phép thử tích phân, chuỗi đã cho là hội tụ.
Xem thêm: