Lập tuyến tính là gì? Xem xong 5 phút hiểu luôn.

Lập trình tuyến tính

Trong Toán học, lập trình tuyến tính là một phương pháp tối ưu hóa các phép toán với một số ràng buộc. Mục tiêu chính của lập trình tuyến tính là tối đa hóa hoặc tối thiểu hóa giá trị số. Nó bao gồm các hàm tuyến tính chịu các ràng buộc ở dạng phương trình tuyến tính hoặc ở dạng bất phương trình.

Lập trình tuyến tính được coi là một kỹ thuật quan trọng được sử dụng để tìm cách sử dụng tài nguyên tối ưu. Thuật ngữ “lập trình tuyến tính” bao gồm hai từ là tuyến tính và lập trình. Từ “tuyến tính” xác định mối quan hệ giữa nhiều biến với bậc một. Từ “lập trình” định nghĩa quá trình lựa chọn giải pháp tốt nhất từ ​​các giải pháp thay thế khác nhau.

Lập trình tuyến tính được sử dụng rộng rãi trong Toán học và một số lĩnh vực khác như kinh tế, kinh doanh, viễn thông và các lĩnh vực sản xuất. Trong bài viết này, chúng ta hãy thảo luận về định nghĩa của lập trình tuyến tính, các thành phần của nó, một phương pháp simplex với các bài toán lập trình tuyến tính.

Lập trình tuyến tính là gì?

Lập trình tuyến tính (LP)   hoặc Tối ưu hóa tuyến tính có thể được định nghĩa là bài toán tối đa hóa hoặc tối thiểu hóa một hàm tuyến tính chịu các ràng buộc tuyến tính. Các ràng buộc có thể là bình đẳng hoặc bất bình đẳng. Các bài toán tối ưu hóa liên quan đến việc tính toán lãi và lỗ.  Các bài toán lập trình tuyến tính  là một loại bài toán tối ưu hóa quan trọng, giúp tìm ra vùng khả thi và tối ưu hóa giải pháp để có giá trị cao nhất hoặc thấp nhất của hàm.

Lập trình tuyến tính là phương pháp xem xét các bất đẳng thức khác nhau liên quan đến một tình huống và tính giá trị tốt nhất cần thiết để đạt được trong các điều kiện đó.

Một số giả định được đưa ra khi làm việc với lập trình tuyến tính là:

• Số lượng các ràng buộc phải được thể hiện bằng các thuật ngữ định lượng
• Mối quan hệ giữa các ràng buộc và hàm mục tiêu phải là tuyến tính
• Hàm tuyến tính (tức là, hàm mục tiêu) phải được tối ưu hóa

Các thành phần của lập trình tuyến tính

Các thành phần cơ bản của LP như sau:

• Các biến quyết định
• Ràng buộc
• Dữ liệu
• Chức năng Mục tiêu

Đặc điểm của lập trình tuyến tính

Sau đây là năm đặc điểm của bài toán lập trình tuyến tính:

Các hạn chế – Các hạn chế cần được thể hiện dưới dạng toán học, liên quan đến tài nguyên.

Hàm mục tiêu – Trong một vấn đề, hàm mục tiêu nên được xác định một cách định lượng.

Tuyến tính – Mối quan hệ giữa hai hoặc nhiều biến trong hàm phải tuyến tính. Có nghĩa là mức độ của biến là một.

Tính hữu hạn – Nên có số lượng đầu vào và đầu ra hữu hạn và vô hạn. Trường hợp hàm số có vô số thừa số thì phương án tối ưu không khả thi.

Không phủ định – Giá trị biến phải dương hoặc bằng không. Nó không được là một giá trị âm.

Biến quyết định – Biến quyết định sẽ quyết định đầu ra. Nó đưa ra giải pháp cuối cùng của vấn đề. Đối với bất kỳ vấn đề nào, bước đầu tiên là xác định các biến quyết định.

Các vấn đề về lập trình tuyến tính

Các vấn đề về lập trình tuyến tính (LPP) là một vấn đề liên quan đến việc tìm giá trị tối ưu của hàm tuyến tính đã cho. Giá trị tối ưu có thể là giá trị lớn nhất hoặc giá trị nhỏ nhất. Ở đây, hàm tuyến tính đã cho được coi là một hàm mục tiêu. Hàm mục tiêu có thể chứa một số biến, tùy thuộc vào các điều kiện và nó phải thỏa mãn tập các bất đẳng thức tuyến tính được gọi là các ràng buộc tuyến tính. Trong lập trình tuyến tính, thuật ngữ “tuyến tính” đại diện cho mối quan hệ toán học được sử dụng trong bài toán đã cho (Nói chung, mối quan hệ tuyến tính) và thuật ngữ “lập trình” đại diện cho phương pháp xác định kế hoạch hành động cụ thể. Các bài toán lập trình tuyến tính có thể được sử dụng để có được giải pháp tối ưu cho các tình huống sau, chẳng hạn như vấn đề sản xuất, vấn đề chế độ ăn uống, vấn đề vận chuyển,

Phương pháp giải quyết vấn đề lập trình tuyến tính

Bài toán lập trình tuyến tính có thể được giải quyết bằng các phương pháp khác nhau, chẳng hạn như phương pháp đồ họa, phương pháp simplex, hoặc bằng cách sử dụng các công cụ như R, open solver, v.v. Ở đây, chúng ta sẽ thảo luận về hai kỹ thuật quan trọng nhất được gọi là phương pháp simplex và phương pháp đồ họa trong chi tiết.

Phương pháp Simplex lập trình tuyến tính

Phương pháp simplex là một trong những phương pháp phổ biến nhất để giải các bài toán lập trình tuyến tính. Đó là một quá trình lặp đi lặp lại để có được giải pháp tối ưu khả thi. Trong phương pháp này, giá trị của biến cơ bản tiếp tục biến đổi để có được giá trị lớn nhất cho hàm mục tiêu. Thuật toán cho phương pháp simplex lập trình tuyến tính được cung cấp dưới đây:

Bước 1 : Thiết lập một bài toán cho trước. (tức là,) viết các ràng buộc bất đẳng thức và hàm mục tiêu.

Bước 2: Chuyển các bất phương trình đã cho thành phương trình bằng cách thêm biến chùng vào mỗi biểu thức bất phương trình.

Bước 3 : Tạo hoạt cảnh đơn giản ban đầu. Viết hàm mục tiêu ở hàng dưới cùng. Ở đây, mỗi ràng buộc bất bình đẳng xuất hiện trong hàng riêng của nó. Bây giờ, chúng ta có thể biểu diễn vấn đề dưới dạng một ma trận tăng cường, được gọi là hoạt cảnh đơn giản ban đầu.

Bước 4 : Xác định mục nhập phủ định lớn nhất ở hàng dưới cùng, giúp xác định cột xoay. Mục nhập âm lớn nhất ở hàng dưới cùng xác định hệ số lớn nhất trong hàm mục tiêu, điều này sẽ giúp chúng ta tăng giá trị của hàm mục tiêu nhanh nhất có thể.

Bước 5 : Tính toán các thương số. Để tính toán thương số, chúng ta cần chia các mục ở cột ngoài cùng bên phải cho các mục trong cột đầu tiên, không bao gồm hàng dưới cùng. Thương số nhỏ nhất xác định hàng. Hàng được xác định trong bước này và phần tử được xác định trong bước sẽ được coi là phần tử xoay.

Bước 6: Tiến hành xoay vòng để tất cả các mục khác trong cột bằng không.

Bước 7: Nếu không có mục nhập âm nào ở hàng dưới cùng, hãy kết thúc quá trình. Nếu không, hãy bắt đầu từ bước 4.

Bước 8: Cuối cùng, xác định giải pháp liên quan đến hoạt cảnh simplex cuối cùng.

Phương pháp đồ họa

Phương pháp đồ họa được sử dụng để tối ưu hóa lập trình tuyến tính hai biến. Nếu bài toán có hai biến quyết định thì phương pháp đồ thị là phương pháp tốt nhất để tìm ra giải pháp tối ưu. Trong phương pháp này, tập các bất đẳng thức phải chịu các ràng buộc. Sau đó, các bất đẳng thức được vẽ trong mặt phẳng XY. Một khi, tất cả các bất bình đẳng được vẽ trong đồ thị XY, vùng giao nhau sẽ giúp quyết định vùng khả thi. Vùng khả thi sẽ cung cấp giải pháp tối ưu cũng như giải thích tất cả các giá trị mà mô hình của chúng ta có thể thực hiện. Hãy để chúng tôi xem một ví dụ ở đây và hiểu khái niệm về lập trình tuyến tính một cách tốt hơn.

Thí dụ:

Tính giá trị lớn nhất và giá trị nhỏ nhất của z = 5x + 3y cho các ràng buộc sau.

x + 2y ≤ 14

3x – y ≥ 0

x – y ≤ 2

Giải pháp:

Ba bất đẳng thức chỉ ra các ràng buộc. Vùng của mặt phẳng sẽ được đánh dấu là vùng khả thi.

Phương trình tối ưu (z) = 5x + 3y. Bạn phải tìm các điểm góc (x, y) cho giá trị lớn nhất và nhỏ nhất của z.

Để bắt đầu, trước tiên hãy giải từng bất đẳng thức.

x + 2y ≤ 14 ⇒  y ≤ – (1/2) x + 7

3x – y ≥ 0 ⇒  y ≤ 3x

x – y ≤ 2 ⇒ y  ≥ x – 2

Đây là đồ thị cho các phương trình trên.

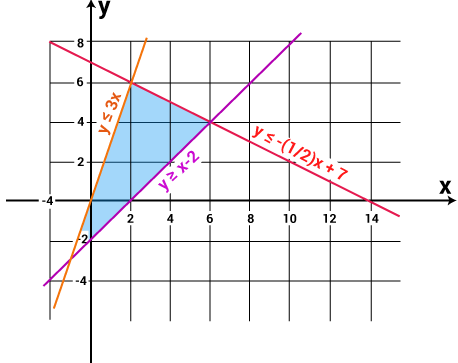
Bây giờ hãy ghép các đường thẳng để tạo thành một hệ phương trình tuyến tính để tìm các điểm góc.

y = – (½) x + 7

y = 3x

Giải các phương trình trên, ta được các điểm ở góc là (2, 6)

y = -1/2 x + 7

y = x – 2

Giải các phương trình trên, ta được các điểm góc là (6, 4)

y = 3x

y = x – 2

Giải các phương trình trên, ta được các điểm ở góc là (-1, -3)

Đối với hệ thống tuyến tính, các giá trị lớn nhất và nhỏ nhất của phương trình tối ưu hóa nằm trên các góc của vùng khả thi. Do đó, để tìm ra phương án tối ưu, bạn chỉ cần cắm ba điểm này vào z = 3x + 4y

(2, 6):

z = 5 (2) + 3 (6) = 10 + 18 = 28

(6, 4):

z = 5 (6) + 3 (4) = 30 + 12 = 42

(–1, –3):

z = 5 (-1) + 3 (-3) = -5 -9 = -14

Do đó, cực đại của z = 42 nằm ở (6, 4) và cực tiểu của z = -14 nằm ở (-1, -3)

Ứng dụng lập trình tuyến tính

Một ví dụ thời gian thực sẽ xem xét những hạn chế của lao động và nguyên vật liệu, đồng thời tìm ra mức sản xuất tốt nhất để có lợi nhuận tối đa trong những trường hợp cụ thể. Nó là một phần của lĩnh vực toán học quan trọng được gọi là kỹ thuật tối ưu hóa. Các ứng dụng của LP trong một số lĩnh vực khác là

• Kỹ thuật – Nó giải quyết các vấn đề về thiết kế và sản xuất vì nó rất hữu ích cho việc tối ưu hóa hình dạng
• Sản xuất hiệu quả – Để tối đa hóa lợi nhuận, các công ty sử dụng biểu thức tuyến tính
• Công nghiệp năng lượng – Nó cung cấp các phương pháp tối ưu hóa hệ thống điện.
• Tối ưu hóa Giao thông – Để có hiệu quả về chi phí và thời gian.

Tầm quan trọng của lập trình tuyến tính

Lập trình tuyến tính được áp dụng rộng rãi trong lĩnh vực tối ưu hóa vì nhiều lý do. Nhiều bài toán chức năng trong phân tích hoạt động có thể được biểu diễn dưới dạng các bài toán lập trình tuyến tính. Một số vấn đề đặc biệt của lập trình tuyến tính như truy vấn luồng mạng và truy vấn luồng đa hàng hóa được coi là quan trọng đã tạo ra nhiều nghiên cứu về các thuật toán chức năng cho giải pháp của chúng.

Các vấn đề về thực hành lập trình tuyến tính

Giải các bài toán lập trình tuyến tính sau:

1. Một bác sĩ muốn trộn hai loại thực phẩm sao cho thành phần vitamin trong hỗn hợp chứa ít nhất 8 đơn vị vitamin A và 10 đơn vị vitamin C. Thực phẩm ‘I’ chứa 2 đơn vị / kg vitamin A và 1 đơn vị. / kg vitamin C. Thực phẩm ‘II’ chứa 1 đơn vị / kg vitamin A và 2 đơn vị / kg vitamin C. Giá 50 Rs / kg để mua Thực phẩm ‘I’ và 70 Rs / kg để mua Thực phẩm ‘II’ . Hình thành bài toán này như một bài toán lập trình tuyến tính để giảm thiểu chi phí của một hỗn hợp như vậy
2. Một loại bánh cần 200g bột và 25g mỡ, một loại bánh khác cần 100g bột và 50g mỡ. Hình thành bài toán này dưới dạng một bài toán lập trình tuyến tính để tìm số bánh tối đa có thể làm được từ 5kg bột mì và 1 kg chất béo giả sử rằng không thiếu các nguyên liệu khác được sử dụng để làm bánh.