Đồ thị là gì
Trong Toán học, biểu đồ là một biểu diễn bằng hình ảnh của bất kỳ dữ liệu nào một cách có tổ chức. Biểu đồ thể hiện mối quan hệ giữa các đại lượng biến thiên. Trong lý thuyết đồ thị, đồ thị đại diện cho một tập hợp các đối tượng, có liên quan với nhau theo một nghĩa nào đó. Các đối tượng về cơ bản là các khái niệm toán học, được biểu thị bằng các đỉnh hoặc các nút và mối quan hệ giữa các cặp nút, được biểu thị bằng các cạnh.
Lịch sử
Lịch sử của lý thuyết đồ thị cho biết nó được đưa ra bởi nhà toán học Thụy Sĩ nổi tiếng tên là Leonhard Euler , để giải quyết nhiều vấn đề toán học bằng cách xây dựng đồ thị dựa trên dữ liệu cho trước hoặc một tập hợp các điểm. Biểu diễn đồ họa cho thấy các loại dữ liệu khác nhau dưới dạng biểu đồ thanh, bảng tần số, biểu đồ đường, biểu đồ hình tròn, biểu đồ đường, v.v.
Định nghĩa
Lý thuyết đồ thị là nghiên cứu về điểm và đường. Trong Toán học, nó là một lĩnh vực phụ liên quan đến việc nghiên cứu các đồ thị. Nó là một biểu diễn bằng hình ảnh đại diện cho sự thật Toán học. Lý thuyết đồ thị là nghiên cứu về mối quan hệ giữa các đỉnh (nút) và các cạnh (đường).
Về mặt hình thức, một đồ thị được biểu thị là một cặp G (V, E).
Trong đó V đại diện cho các đỉnh của tập hữu hạn và E đại diện cho các cạnh của tập hữu hạn.
Do đó, chúng ta có thể nói một đồ thị bao gồm tập các đỉnh V và tập các cạnh E. không rỗng.
Thí dụ
Giả sử, một Đồ thị G = (V, E), trong đó
Các đỉnh, V = {a, b, c, d}
Các cạnh, E = {{a, b}, {a, c}, {b, c}, {c, d}}
Các loại đồ thị
Các biểu đồ về cơ bản có hai loại, có hướng và không có hướng. Nó được hiểu rõ nhất bằng hình dưới đây. Mũi tên trong hình chỉ hướng.
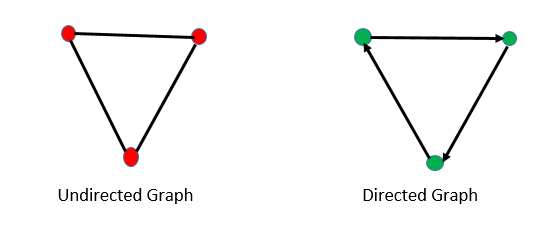

Đồ thị hướng
Trong lý thuyết đồ thị, đồ thị có hướng là đồ thị được tạo thành từ một tập hợp các đỉnh được nối với nhau bởi các cạnh, trong đó các cạnh có hướng liên kết với chúng.
Đồ thị vô hướng
Đồ thị vô hướng được định nghĩa là đồ thị trong đó tập hợp các nút được kết nối với nhau, trong đó tất cả các cạnh đều có hướng. Đôi khi, loại đồ thị này được gọi là mạng vô hướng.
Các loại đồ thị khác
- Null Graph: Một đồ thị không có cạnh.
- Đồ thị đơn giản: Đồ thị vô hướng và không có bất kỳ vòng lặp hoặc nhiều cạnh nào.
- Đa đồ thị: Một đồ thị có nhiều cạnh giữa cùng một tập các đỉnh. Nó có các vòng lặp được hình thành.
- Đồ thị được kết nối: Một đồ thị trong đó hai đỉnh bất kỳ được nối với nhau bằng một đường dẫn.
- Đồ thị ngắt kết nối: Một đồ thị trong đó hai đỉnh hoặc nút bất kỳ bị ngắt kết nối bởi một đường dẫn.
- Đồ thị chu kỳ: Một đồ thị hoàn thành một chu trình.
- Đồ thị hoàn chỉnh: Khi mỗi cặp đỉnh được nối với nhau bằng một cạnh thì đồ thị đó được gọi là đồ thị hoàn chỉnh
- Đồ thị phẳng: Khi không có hai cạnh nào của đồ thị cắt nhau và tất cả các đỉnh và cạnh đều được vẽ trong một mặt phẳng, thì đồ thị như vậy được gọi là đồ thị phẳng
Thuộc tính của đồ thị
- Điểm bắt đầu của mạng được gọi là gốc.
- Khi các loại nút giống nhau được kết nối với nhau, khi đó đồ thị được gọi là đồ thị phân loại, nếu không nó được gọi là đồ thị phân loại.
- Đồ thị chu trình được cho là đồ thị có một chu trình duy nhất.
- Khi tất cả các cặp nút được nối với nhau bằng một cạnh duy nhất, nó sẽ tạo thành một đồ thị hoàn chỉnh.
- Một đồ thị được cho là đối xứng khi mỗi cặp đỉnh hoặc nút được kết nối theo cùng một hướng hoặc theo hướng ngược lại.
- Khi một đồ thị có một đồ thị duy nhất, nó là một đồ thị đường dẫn.
Cây, mức độ và chu kỳ của đồ thị
Có một số thuật ngữ nhất định được sử dụng trong biểu diễn đồ thị như Độ, Cây, Chu kỳ, v.v. Hãy cùng chúng tôi tìm hiểu sơ lược về chúng.
Cây: Cây trong biểu đồ là kết nối giữa các mạng vô hướng chỉ có một đường dẫn giữa hai đỉnh bất kỳ. Nó được giới thiệu bởi nhà toán học người Anh Arthur Cayley vào năm 1857. Cây đồ thị chỉ có các đường thẳng giữa các nút theo bất kỳ hướng cụ thể nào nhưng không có bất kỳ chu trình hoặc vòng lặp nào. Do đó cây cối là đồ thị có hướng.
Mức độ: Một mức độ trong một đồ thị được đề cập là số cạnh được kết nối với một đỉnh. Nó được ký hiệu là deg (v), trong đó v là một đỉnh của đồ thị. Vì vậy, về cơ bản nó là số đo của đỉnh.
Chu trình: Chu trình là một đường khép kín trong đồ thị tạo thành một vòng lặp. Khi điểm bắt đầu và điểm kết thúc giống nhau trong một đồ thị có chứa một tập các đỉnh, thì chu trình của đồ thị được hình thành. Khi không có sự lặp lại của đỉnh trong một mạch kín, thì chu trình là một chu trình đơn giản. Đồ thị chu trình được kí hiệu là C n .
- Một chu trình có số cạnh hoặc số đỉnh là số chẵn được gọi là chu trình chẵn.
- Chu trình có số cạnh hoặc đỉnh là số lẻ được gọi là Chu trình lẻ.
Thuật toán lý thuyết đồ thị
Thủ tục để vẽ một đồ thị cho bất kỳ hàm nào đã cho hoặc để tính một hàm bất kỳ là thuật toán của đồ thị. Về cơ bản, có các bước hoặc tập hợp hướng dẫn được xác định trước phải được tuân theo để giải quyết một vấn đề bằng phương pháp đồ họa. Có nhiều loại thuật toán khác nhau mà lý thuyết đồ thị tuân theo, chẳng hạn như;
- Thuật toán Bellman-Ford
- Thuật toán của Borůvka
- Thuật toán Ford – Fulkerson
- Thuật toán Edmonds – Karp và nhiều thuật toán khác.
Tải xuống Ứng dụng học tập của BYJU và học cách biểu diễn các phương trình toán học dưới dạng đồ thị.