Phân tích nhân tử là gì? Xem xong 5 phút hiểu luôn.

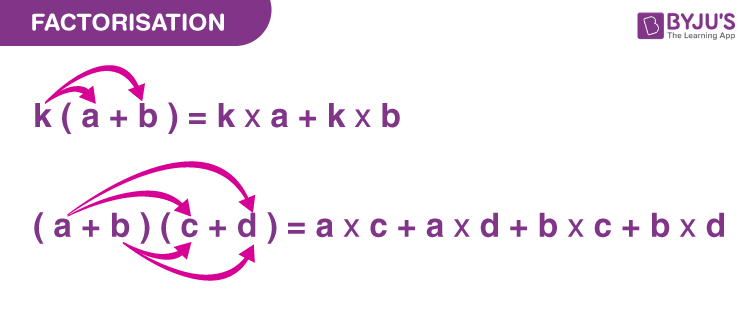
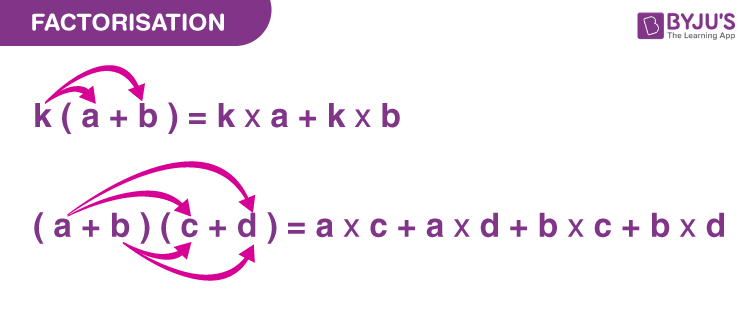
Ví dụ: Thừa số của x ² – 4 là (x – 2) (x + 2). Có nghĩa là cả (x- 2) và (x + 2) đều là thừa số của x ² – 4.

Nó chỉ đơn giản là việc phân giải một số nguyên hoặc đa thức thành các thừa số sao cho khi nhân với nhau chúng sẽ cho kết quả là số nguyên hoặc đa thức ban đầu hoặc ban đầu. Trong phương pháp phân tích nhân tử, chúng ta rút gọn bất kỳ phương trình đại số hoặc bậc hai nào về dạng đơn giản hơn, trong đó phương trình được biểu diễn dưới dạng tích của các thừa số thay vì mở rộng dấu ngoặc. Các thừa số của bất kỳ phương trình nào có thể là một số nguyên, một biến số hoặc một biểu thức đại số .

Sự thừa số trong Toán học

Đối với thừa số, một số có nghĩa là chia nó thành các số có thể nhân lên để có được số ban đầu. Ví dụ,

Ngoài ra, các số có thể được phân tích thành các kết hợp khác nhau. Có nhiều cách khác nhau để tìm thừa số của một con số.   Để tìm thừa số của một số nguyên là một phương pháp dễ dàng nhưng để tìm thừa số của các phương trình đại số không phải là dễ dàng. Vậy chúng ta cùng học tìm nhân tử của đa thức bậc hai. 

Đọc thêm:

• Tính toán đa thức
• Thừa số của biểu thức đại số

Thừa số trong Đại số

Các số 1, 2, 6 và 12 đều là thừa số của 12 vì chúng chia 12 không có dư. Đây là một quá trình quan trọng trong đại số được sử dụng để đơn giản hóa các biểu thức, đơn giản hóa phân số và giải phương trình. Nó còn được gọi là thừa số hóa đại số.

Công thức thừa số cơ bản

• a  ²  – b  ²  = (a – b) (a + b)
• (a + b)  ²  = a  ²  + 2ab + b  ²
• (a – b)  ²  = a  ²  – 2ab + b  ²
• a  ³  – b  ³  = (a – b) (a  ²  + ab + b  ²  )
• a  ³  + b  ³  = (a + b) (a  ²  – ab + b  ²  )
• (a + b + c)  ²  = a  ²  + b  ²  + c  ²  + 2ab + 2bc + 2ca
• (a – b – c)  ²  = a  ²  + b  ²  + c  ²  – 2ab + 2bc – 2ca

Công thức thừa số cho một đa thức bậc hai

“Bậc hai” là một đa thức được viết giống như “ax ² + bx + c”, trong đó “a”, “b” và “c” chỉ là các số. Đối với trường hợp tính toán dễ dàng, bạn có thể xác định hai số sẽ không chỉ nhân với số hạng không đổi “c” mà còn cộng lại với “b” bằng hệ số của số hạng x.

Công thức nhân tử đại số đặc biệt quan trọng khi giải đa thức bậc hai Khi rút gọn công thức chúng ta phải bỏ tất cả các dấu ngoặc, nhưng trong trường hợp cụ thể, chẳng hạn với công thức phân số, đôi khi chúng ta có thể sử dụng thừa số để rút gọn công thức.

Điều khoản và Yếu tố

Điều khoản là gì?

Nó là một cái gì đó sẽ được thêm vào hoặc trừ đi (trừ là thêm một số âm) trong một biểu thức.

Nếu 2x + 7 là một biểu thức thì 2x và 7 là các số hạng.

Tổng = số hạng + số hạng

Yếu tố là gì?

Nó là một cái gì đó được nhân lên trong một biểu thức.

Sản phẩm = yếu tố × yếu tố

Ví dụ :

p = 4 (2q – 6)

4 và 2q – 6 là các thừa số trong khi 2q ​​và 6 là các số hạng.