Phép nhân theo phương pháp vô hướng-Phép toán và các ví dụ

Phép nhân với một vô hướng là một cách thay đổi độ lớn hoặc hướng của một vectơ. Đặt, nó là

“Phép nhân đại lượng vectơ và đại lượng vô hướng.”

Nhớ lại rằng một đại lượng vô hướng chỉ là một số thực. Nhân một vectơ với một đại lượng vô hướng gây ra sự thay đổi trong tỷ lệ của vectơ đó.

Trong chủ đề này, chúng ta sẽ thảo luận về các khía cạnh sau của phép nhân vô hướng:

• Phép nhân vô hướng là gì?
• Làm thế nào để Nhân một Vectơ với một Vô hướng?
• Nhân một vectơ với một vô hướng

Phép nhân vô hướng là gì?

Phép nhân vô hướng bao gồm việc nhân một đại lượng nhất định với một đại lượng vô hướng. Nếu đại lượng đã cho là đại lượng vô hướng, thì phép nhân tạo ra một đại lượng vô hướng khác. Nhưng, nếu đại lượng là một vectơ, thì phép nhân với vô hướng sẽ cho ra một vectơ.

Ví dụ , phép nhân một vô hướng C với một vectơ A sẽ thu được một vectơ khác. Chúng tôi viết hoạt động này là:

C * A = C A

Trong ví dụ trên, vectơ kết quả C A là phiên bản tỷ lệ của vectơ A có độ lớn gấp C lần độ lớn của vectơ A ban đầu . Hướng của nó được xác định bởi giá trị của C theo cách sau:

• Nếu C> 0, thì vectơ kết quả C Asẽ có cùng hướng với vectơ
• Nếu C <0, thì vectơ kết quả là:
  -C * A = –C A
  Dấu âm sẽ đảo ngược hướng của vectơ kết quả so với vectơ tham chiếu
• Nếu C = 0, thì phép nhân tạo ra một vectơ 0 là:
  0 * A = 0

Lưu ý rằng nếu C = 1, thì nhân bất kỳ vectơ nào với C sẽ giữ cho vectơ đó không đổi.

1 * A = A

Làm thế nào để Nhân một Vectơ với một Vô hướng?

Giả sử một vectơ P được biểu diễn dưới dạng vectơ cột:

P = (x1, y1).

Nhân nó với một vô hướng có nghĩa là chia tỷ lệ từng thành phần của vectơ P với C như sau:

C * P = C (x1, y1)

C * P = (Cx1, Cy1)

Bây giờ, độ lớn của vectơ kết quả có thể được tìm thấy giống như cách mà chúng ta có thể tìm độ lớn của vectơ P:

| C * P | = √ (Cx1) ^ 2 + (CX2) ^ 2

Nhân một vectơ với một vô hướng

Trong phần này, chúng ta sẽ thảo luận về một số tính chất quan trọng của phép nhân vô hướng. Lưu ý rằng các thuộc tính này đúng cho dù một đại lượng vô hướng được nhân với một vectơ hay với một đại lượng vô hướng khác.

Đầu tiên chúng ta hãy xem xét hai vectơ, A và B, và hai vô hướng, c, và d. Sau đó, các thuộc tính sau giữ:

1. | c A | = | c | * | A |. Độ lớn của vectơ tỷ lệ kết quả bằng giá trị tuyệt đối của vectơ vô hướng nhân với độ lớn.
2. Thuộc tính liên kết: c (d B ) = (cd) * B
3. Tính chất giao hoán: c * A = A * c
4. Thuộc tính phân phối: (c + d) A = c * A + d * A

d * ( A + B ) = d * A + d * B

Các ví dụ

Trong phần này, chúng ta sẽ thảo luận về một số ví dụ và các giải pháp từng bước của chúng để giúp hiểu rõ hơn về phép nhân vô hướng.

ví dụ 1 

Một ô tô đang chuyển động với vận tốc V = 30 m / s hướng Bắc. Xác định véc tơ gấp đôi véc tơ này.

Giải pháp

Từ dữ liệu đã cho, chúng tôi có thông tin sau:

V = 30 m / s hướng Bắc.

Để xác định vectơ bằng hai lần vectơ này, chúng ta nhân vectơ đã cho với giá trị vô hướng 2. Điều này cho chúng ta:

2 * V = 2 * (30 m / s)

2 V = 60 m / s, hướng Bắc

Vì giá trị vô hướng đã cho là dương nên hướng của V không bị ảnh hưởng . Tuy nhiên, nó thay đổi độ lớn của nó thành hai lần giá trị ban đầu. Như vậy ô tô sẽ chuyển động thẳng Bắc với vận tốc gấp đôi vận tốc ban đầu.

Ví dụ 2

Cho vectơ S = (2, 3), xác định và vẽ 2 * S. Độ lớn và hướng của vectơ 2 S là ?

Giải pháp

Vectơ S đã cho là một vectơ cột và đại lượng vô hướng là 2. Nhân vectơ S với 2 cho ta:

2 * S = 2 * (2, 3)

Nhân mỗi thành phần của vectơ S với 2 ta được:

2 * S = (2 * 2, 2 * 3)

2 * S = (4, 6).

Tiếp theo, chúng tôi xác định và so sánh độ lớn của cả hai vectơ:

| S | = √2 ^ 2 + 3 ^ 2

| S | = √4 + 9

| S | = √13

Độ lớn của vectơ 2 S là:

| 2 S | = √4 ^ 2 + 6 ^ 2

| 2 S | = √16 + 36

| 2 S | = √52

| 2 S | = √4 * 13

| 2 S | = 2 * (√13)

Có thể nhận thấy rõ ràng từ phương trình cuối cùng rằng phép nhân vô hướng đã làm cho độ lớn của vectơ S tăng gấp đôi .

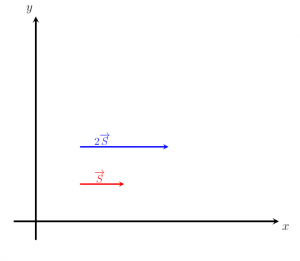
Những hình ảnh dưới đây hiển thị hai vectơ, S và 2 S . Có thể thấy rằng sự chỉ đạo của vector 2 S là song song với đó của vector S . Điều này xác minh thêm rằng việc chia tỷ lệ một vectơ bằng một đại lượng dương chỉ làm thay đổi độ lớn và không thay đổi hướng.

Ví dụ 3

Cho một véc tơ S = (2, 3), xác định và phác thảo -2 * S. Tìm độ lớn và hướng của vector -2 S .

Giải pháp

Vectơ S đã cho là một vectơ cột và đại lượng vô hướng là 2. Nhân vectơ S với 2 cho ta:

-2 * S = -2 * (2, 3)

Nhân mỗi thành phần của vectơ S với 2 ta được:

-2 * S = (-2 * 2, -2 * 3)

-2 * S = (-4, -6).

Tiếp theo, chúng tôi xác định và so sánh độ lớn của cả hai vectơ:

| S | = √2 ^ 2 + 3 ^ 2

| S | = √4 + 9

| S | = √13

Độ lớn của vectơ -2 S là:

| -2 S | = √ (-4) ^ 2 + (-6) ^ 2

| -2 S | = √16 + 36

| -2 S | = √52

| -2 S | = √4 * 13

| -2 S | = 2 * (√13)

Nó có thể được quan sát thấy rõ ràng từ phương trình cuối cùng mà nhân vô hướng đã tăng gấp đôi độ lớn của vector S . Ngoài ra, dấu âm không ảnh hưởng đến độ lớn của vectơ -2 S.

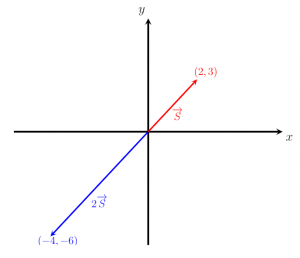
Những hình ảnh dưới đây hiển thị hai vectơ S và -2 S. Có thể thấy rằng sự chỉ đạo của vector -2 S là đối diện của vector S . Điều này xác minh thêm rằng việc chia tỷ lệ một vectơ bằng một đại lượng âm không ảnh hưởng đến độ lớn của nó (tức là, 2 vectơ 2 S và -2 S có cùng độ lớn) nhưng đảo ngược hướng.

Ví dụ 4

Cho một vector Một = (-4, 6), xác định và phác họa vector 1/2 * Một .

Giải pháp

Vectơ A đã cho là một vectơ cột và đại lượng vô hướng là 1/2. Nhân vectơ A với 1/2 cho ta:

1/2 * A = 1/2 * (-4, 6).

Việc đơn giản hóa mang lại cho chúng ta:

1/2 * A = (1/2 * (- 4), 1/2 * (6))

1/2 * A = (-2, 3).

Tiếp theo, chúng tôi xác định và so sánh độ lớn của cả hai vectơ:

| A | = √-4 ^ 2 + 6 ^ 2

| A | = √16 + 36

| A | = √52

| A | = 2 * (√13)

Độ lớn của vectơ 1/2 A là:

| 1/2 A | = √-2 ^ 2 + 3 ^ 2

| 1/2 A | = √4 + 9

| 1/2 A | = √13

Phép nhân vô hướng với giá trị bằng một nửa do đó làm giảm một nửa độ lớn của vectơ ban đầu.

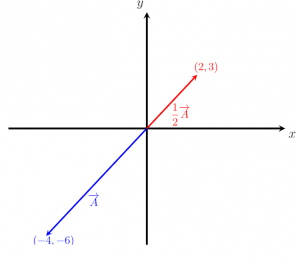
Hình ảnh cho dưới đây cho thấy hai vectơ A và ½ A. Cả hai vectơ có cùng phương nhưng độ lớn khác nhau.

Ví dụ 5

Cho vectơ m = 5i + 6j +3 trong hệ trực giao, hãy xác định vectơ kết quả nếu m nhân với 7.

Giải pháp

Trong trường hợp này, vectơ kết quả có thể nhận được bằng cách chỉ cần nhân vectơ đã cho với 7:

7 m = 7 * (5i + 6j +3)

7 m = (7 * 5i + 7 * 6j + 7 * 3)

7 m = 35i + 42j + 21

Vectơ kết quả có độ lớn gấp 7 lần vectơ ban đầu m nhưng không thay đổi hướng.

Câu hỏi thực hành

1. Cho vectơ M = 10 m Đông, xác định vectơ kết quả thu được bằng cách nhân vectơ đã cho với 3.
2. Cho vectơ N = 15 m North, xác định vectơ kết quả thu được bằng cách nhân vectơ đã cho với -4.
3. Cho u = (-1, 4). Tìm 5 u .
4. Cho v = (3, 9). Tìm -1/3 v .
5. Cho vectơ b = -3i + 2j +2 trong hệ trực giao, tìm 5 b .

Câu trả lời

1. 3 M = 30 m, hướng Đông.
2. -4 N = -60 m, hướng Nam.
3. 5 u = (-5, 20), | u | = √17, | 5 u | = 5 * √17. Phương của u và 5 u giống nhau.
4. -1/3 v = (-1, -3), | v | = 3 * √10, | -1/3 v | = √10, hướng của vectơ -1/3 v ngược với hướng của vectơ v .
5. 5 b = -15i + 10j + 10

Xem thêm:

Hướng của một vectơ là gì? Những ví dụ dễ nhất cho người mới

Hướng dẫn phép cộng vectơ nhanh chóng, dễ hiểu nhất