Định nghĩa Giải tích

Trong toán học, giải tích là một nhánh liên quan đến việc tìm kiếm các tính chất khác nhau của tích phân và đạo hàm của các hàm số. Nó dựa trên sự tổng kết của sự khác biệt nhỏ. Giải tích là nghiên cứu về sự thay đổi liên tục của một hàm hoặc tốc độ thay đổi của một hàm. Nó có hai nhánh chính và hai lĩnh vực đó có liên quan với nhau theo định lý cơ bản của giải tích . Hai nhánh khác nhau là:

• Phép tính vi phân
• Tích phân tích

Trong bài viết này, chúng ta sẽ thảo luận chi tiết các khái niệm cơ bản về phép tính vi phân, công thức và các ví dụ về phép tính vi phân.

Khái niệm cơ bản về phép tính vi phân

Trong kiến ​​thức cơ bản về phép tính vi phân, bạn có thể đã học về phương trình vi phân, đạo hàm và các ứng dụng của đạo hàm. Với bất kỳ giá trị nào cho trước, đạo hàm của hàm được định nghĩa là tốc độ thay đổi của hàm đối với các giá trị đã cho. Phân biệt là một quá trình mà chúng ta tìm đạo hàm của một hàm. Hãy để chúng tôi thảo luận về các thuật ngữ quan trọng liên quan đến các khái niệm cơ bản về phép tính vi phân.

Chức năng

Một hàm được định nghĩa là một quan hệ từ một tập hợp các đầu vào đến một tập hợp các đầu ra, trong đó mỗi đầu vào được liên kết chính xác với một đầu ra. Hàm được biểu diễn bằng “f (x)”.

Biến phụ thuộc

Biến phụ thuộc là một biến mà giá trị của nó luôn phụ thuộc và được xác định bằng cách sử dụng biến còn lại được gọi là biến độc lập. Biến phụ thuộc còn được gọi là biến kết quả. Kết quả đang được đánh giá từ biểu thức toán học bằng cách sử dụng một biến độc lập được gọi là một biến phụ thuộc.

Biến độc lập

Các biến độc lập là đầu vào cho các hàm xác định số lượng đang được thao tác trong một thử nghiệm. Chúng ta hãy xem xét một ví dụ y = 3x. Ở đây, x được gọi là biến độc lập và y được gọi là biến phụ thuộc vì giá trị của y hoàn toàn phụ thuộc vào giá trị của x.

Tên miền và phạm vi

Miền của một hàm được định nghĩa đơn giản là các giá trị đầu vào của một hàm và phạm vi được xác định là giá trị đầu ra của một hàm. Lấy ví dụ, nếu f (x) = 3x là một hàm, miền giá trị hoặc giá trị đầu vào là {1, 2, 3} thì phạm vi của một hàm được cho là

f (1) = 3 (1) = 3

f (2) = 3 (2) = 6

f (3) = 3 (3) = 9

Do đó, phạm vi của hàm sẽ là {3, 6, 9}.

Hạn mức

Giới hạn là một điều quan trọng trong giải tích. Giới hạn được sử dụng để xác định tính liên tục, tích phân và đạo hàm trong giải tích. Giới hạn của một hàm được xác định như sau:

Chúng ta hãy coi hàm là “f” được xác định trên một khoảng mở nào đó có chứa một số số, chẳng hạn như “a”, ngoại trừ có thể tại chính “a”, khi đó giới hạn của hàm f (x) được viết là:

, iff   cho  e  > 0, tồn tại  d  > 0 sao cho 0 <| x – a | <  d  ngụ ý rằng | f (x) – L | <  elimx → af( x ) = L

Có nghĩa là giới hạn f (x) khi “x” tiến tới “a” là “L”

Khoảng thời gian

Một khoảng được định nghĩa là phạm vi số tồn tại giữa hai số đã cho. khoảng thời gian có thể được phân thành hai loại cụ thể là:

• Open Interva l – Khoảng mở được định nghĩa là tập hợp tất cả các số thực x sao cho a <x <b. Nó được biểu diễn là (a, b)
• Khoảng đóng – Khoảng đóng được định nghĩa là tập hợp tất cả các số thực x sao cho a ≤ x và x ≤ b, hay ngắn gọn hơn, a ≤ x ≤ b, và nó được biểu diễn bằng [a, b]

Các dẫn xuất

Công cụ cơ bản của phép tính vi phân là đạo hàm. Đạo hàm được sử dụng để hiển thị tỷ lệ thay đổi. Nó giúp hiển thị số tiền mà hàm đang thay đổi cho một điểm nhất định. Đạo hàm được gọi là hệ số góc. Nó đo độ dốc của đồ thị của một hàm số. Nó xác định tỷ lệ giữa sự thay đổi giá trị của một hàm so với sự thay đổi của biến độc lập. Đạo hàm của y đối với x được biểu thị bằng dy / dx.

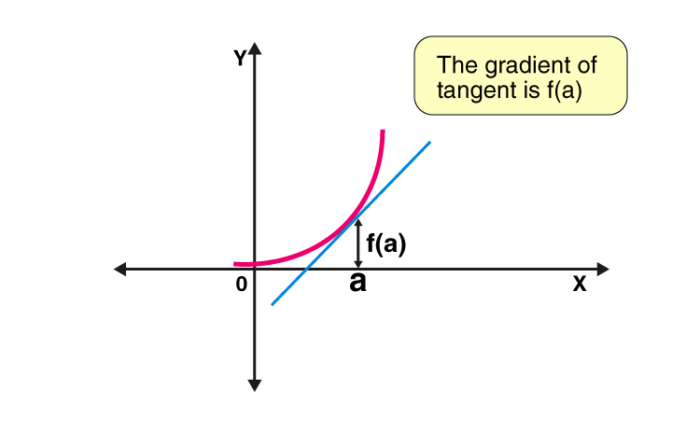
Về mặt hình ảnh, chúng ta định nghĩa đạo hàm là hệ số góc của tiếp tuyến gặp nhau tại một điểm trên đường cong hoặc cho đạo hàm tại điểm mà tiếp tuyến gặp đường cong. Khác biệt hóa có nhiều ứng dụng trong các lĩnh vực khác nhau. Kiểm tra tốc độ thay đổi nhiệt độ của khí quyển hoặc suy ra các phương trình vật lý dựa trên phép đo và đơn vị, v.v., là những ví dụ phổ biến.

Các ví dụ

1. f (x) = 6x ² -2 ⇒ f ‘(x) = 12x
2. f (x) = 2x ⇒ f ‘(x) = 2
3. f (x) = x ³ + 2x ⇒ f ‘(x) = 3x ² + 2