Phương trình của một mặt phẳng: 3 điểm không thẳng hàng là gì? xem xong hiểu luôn.

Các đại lượng vật lý có độ lớn, cũng như gắn trực tiếp với chúng, được gọi là vectơ. Vectơ vị trí chỉ đơn giản biểu thị vị trí hoặc vị trí của một điểm trong hệ Descartes ba chiều liên quan đến một gốc tham chiếu. Trong phần thảo luận sắp tới, chúng ta sẽ nghiên cứu về vectơ và phương trình Descartes của một mặt phẳng trong không gian ba chiều.Trong phần trước, chúng ta đã thảo luận rằng đối với một vectơ đã cho có vô số mặt phẳng vuông góc với nó. Nhưng đối với một điểm cụ thể, tồn tại một và chỉ một mặt phẳng duy nhất vuông góc với nó đi qua điểm đã cho. Phương trình vectơ của một mặt phẳng trong trường hợp này được cho là

[latex] (\ vec {r} – \ vec {a}). \ vec {N} = 0 [/ latex]

Ở đây, [latex] \ vec {r} [/ latex] và [latex] \ vec {a} [/ latex] đại diện cho các vectơ vị trí.

Phương trình Descartes của một mặt phẳng như vậy được biểu diễn bằng:

[latex] A (x- {x} _ {1}) + B (y- {y} _ {1}) + C (z – {z} _ {1}) = 0 [/ latex]

Ở đây, A, B và C là tỷ lệ hướng.

Bây giờ chúng ta hãy thảo luận về phương trình của một mặt phẳng đi qua ba điểm không thẳng hàng.

Phương trình của một mặt phẳng đi qua ba điểm Không thẳng hàng

Chúng ta hãy xem xét ba điểm không thẳng hàng P, Q, R nằm trên một mặt phẳng sao cho vectơ vị trí của chúng được cho bởi [latex] \ vec {a} [/ latex] , [latex] \ vec {b} [/ latex] và [latex] \ vec {c} [/ latex] như trong hình bên dưới.

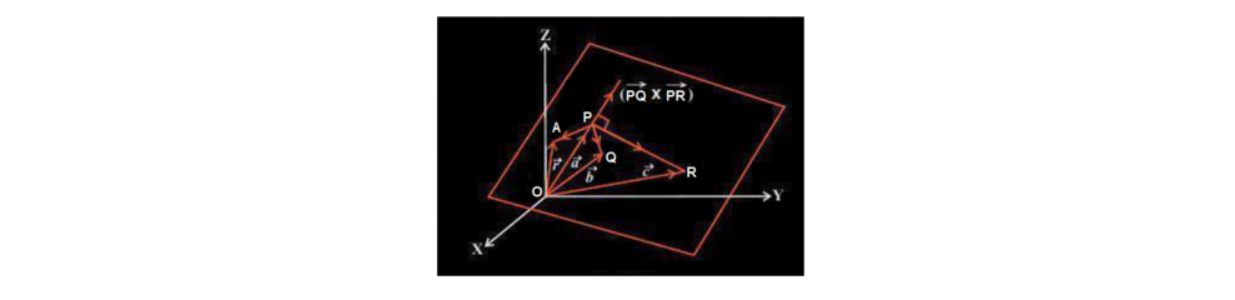
Phương trình của một mặt phẳng: 3 điểm không thẳng hàng

Các vectơ [latex] \ vec {PQ} [/ latex] và [latex] \ vec {PR} [/ latex] nằm trong cùng một mặt phẳng. Vectơ nằm vuông góc với mặt phẳng chứa các điểm P, Q và R được cho bởi [latex] \ vec {PQ} [/ latex] × [latex] \ vec {PR} [/ latex] . Nếu vectơ vị trí của một điểm A bất kỳ nằm trong mặt phẳng chứa P, Q, R thì sử dụng phương trình vectơ của một mặt phẳng như đã nói ở trên, phương trình của mặt phẳng đi qua P và vuông góc với vectơ [latex] \ vec { PQ} [/ latex] × [latex] \ vec {PR} [/ latex] được cung cấp bởi

( [latex] \ vec {r} [/ latex] – [latex] \ vec {a} [/ latex] ). ( [latex] \ vec {PQ} [/ latex] × [latex] \ vec {PR}) = 0 [/ latex]

Ngoài ra, từ hình trên, và. Thay các giá trị này vào phương trình trên, chúng ta có

[latex] (\ vec {r} – \ vec {a}). [(\ vec {b} – \ vec {a}) × (\ vec {c} – \ vec {a})] = 0 [/ mủ cao su]

Điều này biểu diễn phương trình của một mặt phẳng ở dạng vectơ đi qua ba điểm không thẳng hàng.

Để chuyển đổi phương trình này trong hệ Descartes, chúng ta hãy giả sử rằng tọa độ của các điểm P, Q và R được cho là (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) và (x ₃ , y ₃ , z ₃ ) lần lượt. Cũng cho tọa độ của điểm A là x, y và z.