| Các ví dụ | ||||
| 23 | -12 | 6,99 | 5/2 | π (3,14) |
Contents
Định nghĩa số thực
Số thực có thể được định nghĩa là hợp của cả số hữu tỉ và số vô tỉ. Chúng có thể là cả dương hoặc âm và được biểu thị bằng ký hiệu “R”. Tất cả các số tự nhiên, số thập phân và phân số đều thuộc loại này. Xem hình bên dưới, cho thấy sự phân loại các số thực.
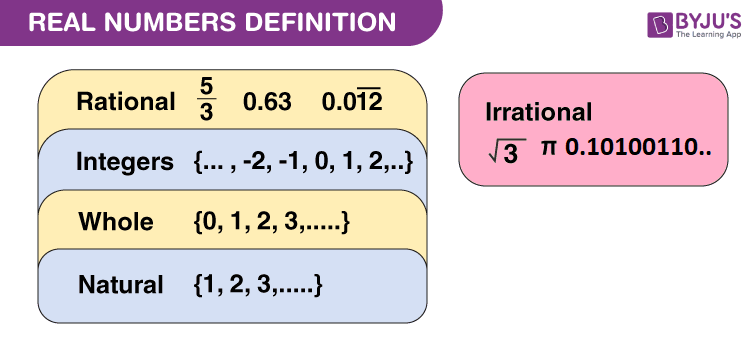

Bộ số thực
Tập hợp các số thực bao gồm các loại khác nhau, chẳng hạn như số tự nhiên và số nguyên, số nguyên, số hữu tỉ và số vô tỉ. Trong bảng dưới đây, tất cả các số này được xác định bằng các ví dụ.
| thể loại | Định nghĩa | Thí dụ |
|---|---|---|
| Số tự nhiên | Chứa tất cả các số đếm bắt đầu từ 1.
N = {1,2,3,4, ……} |
Tất cả các số như 1, 2, 3, 4,5,6,… ..… |
| Số nguyên | Tập hợp số 0 và số tự nhiên.
W = {0,1,2,3,… ..} |
Tất cả các số bao gồm 0 như 0, 1, 2, 3, 4,5,6,… ..… |
| Số nguyên | Kết quả chung của các số nguyên và âm của tất cả các số tự nhiên. | Bao gồm: -infinity (- ∞) , …… ..- 4, -3, -2, -1, 0, 1, 2, 3, 4, …… + infinity (+ ∞) |
| Số hợp lý | Các số có thể viết dưới dạng p / q, trong đó q ≠ 0. | Ví dụ về số hữu tỉ là ½, 5/4 và 12/6, v.v. |
| Số vô tỉ | Tất cả các số không hữu tỉ và không thể viết dưới dạng p / q. | Các số vô tỉ có bản chất không tận cùng và không lặp lại như √2 |
Biểu đồ số thực
Biểu đồ cho tập hợp các số thực bao gồm tất cả các loại được đưa ra dưới đây:
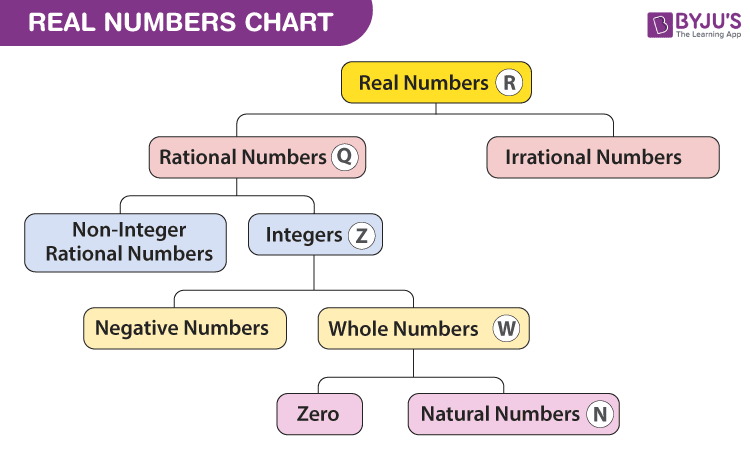

Thuộc tính của số thực
Có bốn thuộc tính chính bao gồm tài sản giao hoán, tài sản liên kết, tài sản phân phối và tài sản nhận dạng. Coi “m, n và r” là ba số thực. Sau đó, các thuộc tính trên có thể được mô tả bằng cách sử dụng m, n và r như hình dưới đây:
Tính chất giao hoán
Nếu m và n là các số thì dạng tổng quát sẽ là m + n = n + m đối với phép cộng và mn = nm đối với phép nhân.
- Phép cộng: m + n = n + m. Ví dụ: 5 + 3 = 3 + 5, 2 + 4 = 4 + 2
- Phép nhân: m × n = n × m. Ví dụ: 5 × 3 = 3 × 5, 2 × 4 = 4 × 2
Bất động sản kết hợp
Nếu m, n và r là các số. Dạng tổng quát sẽ là m + (n + r) = (m + n) + r đối với phép cộng (mn) r = m (nr) đối với phép nhân.
- Phép cộng : Dạng tổng quát sẽ là m + (n + r) = (m + n) + r. Một ví dụ về thuộc tính liên kết cộng là 10 + (3 + 2) = (10 + 3) + 2.
- Phép nhân: (mn) r = m (nr). Một ví dụ về thuộc tính kết hợp nhân là (2 × 3) 4 = 2 (3 × 4).
Thuộc tính phân tán
Đối với ba số m, n và r, có bản chất là thực, thuộc tính phân phối được biểu diễn dưới dạng:
m (n + r) = mn + mr và (m + n) r = mr + nr.
- Ví dụ về thuộc tính phân phối là: 5 (2 + 3) = 5 × 2 + 5 × 3. Ở đây, cả hai bên sẽ mang lại 25.
Thuộc tính nhận dạng
Có tính chất cộng và phép nhân.
- Ngoài ra: m + 0 = m. (0 là danh tính phụ gia)
- Đối với phép nhân: m × 1 = 1 × m = m. (1 là số nhân)
Câu hỏi thực hành
- Hợp số nào nhỏ nhất?
- Chứng minh rằng mọi số nguyên dương lẻ có dạng 6x + 1, 6x + 3 hoặc 6x + 5.
- Đánh giá 2 + 3 × 6 – 5
- Tích của một số hữu tỉ khác 0 và một số vô tỉ là gì?
- Mọi số nguyên dương có thể được biểu diễn dưới dạng 4x + 2 (với x là số nguyên) không?
Số thực Lớp 9 và 10
Trong số thực Lớp 9, các khái niệm phổ biến được giới thiệu bao gồm biểu diễn các số thực trên một trục số, các phép toán trên số thực, các tính chất của số thực và luật số mũ đối với số thực. Trong lớp 10, một số khái niệm nâng cao liên quan đến số thực được đưa vào. Ngoài số thực là gì, học sinh cũng sẽ học về Bổ đề chia của Euclid, Thuật toán chia Euclid và định lý cơ bản của số học ở lớp 10.
Các câu hỏi thường gặp
Số tự nhiên và số thực là gì?
Số tự nhiên là tất cả các số nguyên dương bắt đầu từ 1 đến vô cùng. Tất cả các số tự nhiên đều là số nguyên nhưng không phải tất cả các số nguyên đều là số tự nhiên. Đây là tập hợp tất cả các số đếm như 1, 2, 3, 4, 5, 6, 7, 8, 9, …… .∞.
Số thực là số bao gồm cả số hữu tỉ và số vô tỉ. Các số hữu tỉ như số nguyên (-2, 0, 1), phân số (1/2, 2,5) và số vô tỉ như √3, π (22/7), v.v., đều là số thực.
Số không là số thực hay số ảo?
Số 0 được coi là cả số thực và số ảo. Như chúng ta đã biết, số ảo là căn bậc hai của các số thực không dương. Và vì 0 cũng là một số không dương, do đó nó đáp ứng các tiêu chí của số ảo. Trong khi 0 cũng là một số hữu tỉ, được xác định trong một trục số và do đó là một số thực.
Có những Con số Thực nào không phải là Hợp lý hoặc Phi lý trí?
Không, không có số thực nào là số hữu tỉ và vô tỉ. Bản thân định nghĩa về số thực đã nói lên rằng, nó là sự kết hợp của cả số hữu tỉ và số vô tỉ.
Số thực có phải là tập con của số phức không?
Đúng, bởi vì một số phức là sự kết hợp của một số thực và số ảo. Vì vậy, nếu số phức là một tập hợp thì số thực và số ảo là các tập con của nó.
Xem thêm:







