Tâm đường tròn nội tiếp tam giác rễ học nhất

Đường tròn trong toán hình là một định nghĩa khá khó bao gồm nhiều định nghĩa và công thức khác nhau. Các bài tập về xác định tâm đường tròn nội tiếp tam giác đã gây cho học sinh không ít khó khăn trong giải bài tập. đừng lo điều đó tintuctuyensinh ở đây là để giúp bạn.

Cùng nhau ôn về tâm ĐT nt tam giác ngày nào.

1. định nghĩa về tâm ĐT nt tam giác

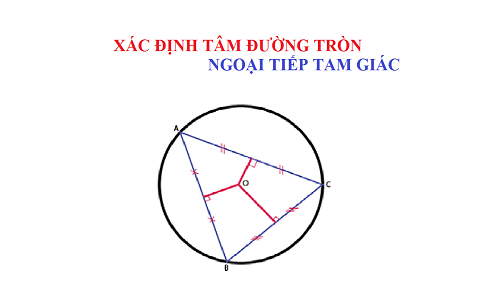
tổng quát tâm ĐT nt tam giác:

Trong hình học, ĐT nt của một tam giác là ĐT lớn nhất nằm trong tam giác; nó tiếp xúc với cả ba cạnh của tam giác. 

Tâm của ĐT nt là giao điểm của ba đường phân giác trong.

Muốn xác định tâm ĐT nội tiếp của tam giác thì các bạn học sinh cần lưu ý phần đã nêu trong lý thuyết như sau: – Tâm đường tròn nội tiếp của tam giác là giao điểm của ba đường phân giác bên trong của tam giác (cũng có thể là giao điểm 2 đường phân giác)

Cách xác định tâm đường tròn nội tiếp tam giác

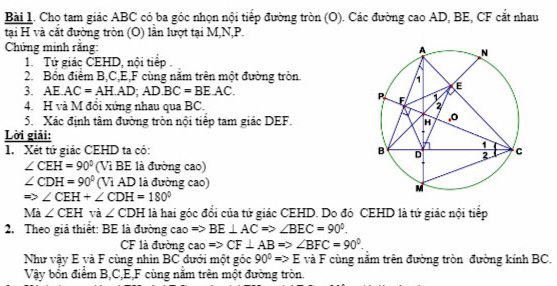
2 cách xác định tâm đường tròn nội tiếp tam giác:

Cách 1: Gọi D,E,F là chân đường PG trong của tam giác ABC kẻ lần lượt từ A,B,C

• Bước 1 :  lần lượt tính độ dài các cạnh tam giác
• Bước 2 : Tính ts k1=ABAC, k2=BABC, k3=CACB
• Bước 3 : Tìm TĐ các điểm D, E, F
• Bước 4: Viết PT đường thẳng AD,BE
• Bước 5: Tâm của ĐT nt tam giác ABC là giao điểm của cạnh AD và cạnh BE

Cách 2: Trong mặt mp Oxy, ta có thể xác định tọa độ  I như sau:

X(I)=BC.x(A)+CA.x(B)+AB.x(CBC)+CA+AB

Y(I)=BC.y(A)+CA.y(B)+AB.y(CBC)+AC+BC

BK ĐT nt tam giác

Phương trình tâm đường tròn nội tiếp tam giác

Cho tam giác ABC có điểm A(xa;ya),

Điểm B(xb;yb)

Điểm C(xC;yC)

Cách 1:

1. Viết PT hai đường phân giác trong góc A và B
2. Tâm I là giao điểm của hai đường PG trên
3. Tính kc từ I đến một cạnh của tam giác ta được BK Viết phương trình ĐT

Cách 2:

1. Viết Phân G đường phân giác trong của đỉnh A
2. Tìm tọa độ chân đường PG trong đỉnh A
3. Gọi I là tâm ĐT, tọa độ điểm I TM hệ thức ID=−BDBA→IA
4. Tính KC từ I đến một cạnh của tam giác
5. Viết PT ĐT

Ví Dụ 1: tìm tâm và BK đường tròn nt tam giác ABC biết

A(11;−7),

  B(23;9) , 

C(−1;2)
ta Dễ dàng viết được PT đoạn  thẳng AB như sau :
4x−3y−65=04x−3y−65=0
ta suy ra PT đoạn AC là:
9x+12y−15=09x+12y−15=0

PT đường phân giác góc A là:

|4x−3y−65|5=|9x+12y−15|15

Từ đó ta rút ra được 2 PT đường phân giác :
3x−21y−180=0
Hoặc 21x+3y−21=0 (Δ2)

Xét (Δ1) : f(x,y)=3x−21y−180
f(xB,yB)=−323
f(xC,yC)=−255

ta suy ra f(xB,yB).f(xC,yC)≥0 

Suy ra B, C nằm cùng phía với đường thẳng (Δ1)

suy ra PT đường phân giác trong góc A là : 

21x+3y−210=021x+3y−210=0 (Δ2)

Hoàn toàn tương tự ta suy ra PT đường phân giác trong góc B là: 27x−39y−270=027x−39y−270=0 (Δ3)(Δ3)

Gọi I là tâm đường tròn NT ΔABC

 hay I là giao điểm 2 đường phân giác trong (Δ2) và (Δ3)
Từ đó tọa độ của điểm I là nghiệm hệ pt:
{21x+3y−210=027x−39y−270=0
suy ra{x=10y=0

vậy tâm I có tọa độ là (10;0)

từ tâm I dùng công thức kc đến các cạnh tam giác ABC 

 suy ra Bán K bằng 5.

Các dạng bài tập khác nhau về tâm đường tròn nội tiếp tam giác.

Dưới đây là một số dạng bài tập cung nhau tham khảo nào

Bài tập 1. Trong mp Oxy cho tam giác ABC với A(–2;3), B(1/4; 0) và C(2;0)

Tìm tâm ĐT nt tam giác ABC.

Bài tập 2.Trong mp Oxy cho tam giác ABC với A(2;6), B(–3;–4) và C(5;0)

1. TG  ABC vuông là tam giác gì?
2. Tìm tâm của ĐT nt tam giác ABC.

Đáp số: kết quả J(2;1)

Bài tập  3. Trong mp Oxy cho tam giác ABC với A(1; 5), B(3;–1) và C(6;0).

Tìm chân ĐC B’ kẻ từ B xuống CA.

Bài tập 4. Trong mp Oxy cho 2 điểm A(2;1) B(–2;4).

 Gọi H là HC của O lên AB. Tìm tọa độ H.

Đáp số:  có kết quả là H(6/5; 8/5).

Bài tập 5. Trong mp Oxy cho tam giác ABC với A(3;–4) B(–4;–2) và C(1;3). Tìm chân ĐC điểm A’ của đường cao kẻ từ A lên BC.

Đáp số:có kết quả là A’(-37/53; -156/53)

Bài tập 6. Trong mp Oxy cho tam giác ABC với A(1;5), B(–4;–5) và C(4;-1). Tìm tâm J của đường tròn nt tam giác ABC.

Đáp Số:có kết quả là J(1;0)

Bài tập 7. Trong mp Oxy cho tam giác ABC với A(-15/2; 2), B(12; 15)và C(0; -3). Tìm tâm J của ĐT nt tam giác ABC.

Đáp số có kết quả là J(-1;2)

Bài tập  8. Trong mp Oxy cho tam giác ABC với A(3;–1), B(1;5) và C(6;0). Gọi A’ là chân Đc kẻ từ A lên BC 

Hãy tìm điểm A’.

Đáp Số: có kết quả là A’(5;1)

Trên đây là khái niệm về đường tròn nội tiếp các cách xác định tâm đường tròn nội tiếp tam giác. Phương pháp giải bài tập về ĐT nội tiếp tam giác mà các học sinh cần nắm chắc và học thuộc để có thể giải được bài tập. 

Tâm đường tròn nội tiếp tam giác là một dạng BT quan trọng trong chương trình học môn toán hình.  Việc Nắm chắc các dạng KT và kĩ năng thực hành làm các BT khác nhau sẽ giúp các bạn học sinh có kết quả cao trong các bài kiểm tra, thi cuối kì.

Cùng đồng hành với tintuctuyensinh để học thật tốt toán hình nhé.

Xem thêm: 

Mở bài kết bài Vợ Nhặt hay nhất 2021

Phân tích hình tượng người lái đò trong tùy bút Người lái đò sông đà hay nhất 2021

Sơ Đồ Tư Duy Ai Đặt Tên Cho Dòng Sông dễ hiểu nhất 2021