Tam giác góc phải là gì? Xem xong 5 phút hiểu luôn.

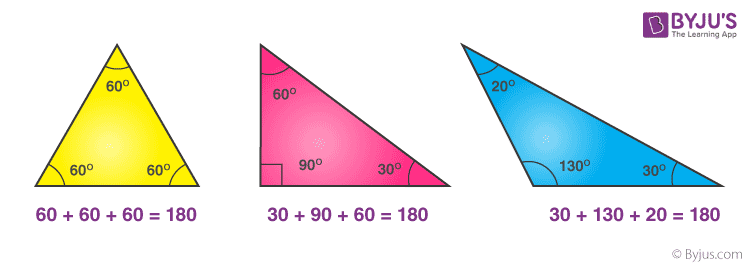
Là một hình khép kín, một hình tam giác có thể có nhiều dạng khác nhau và mỗi hình dạng được mô tả bằng góc tạo bởi hai cạnh bất kỳ.

Phép cộng và phép trừ ma trận là gì? Xem xong 5 phút hiểu luôn.

Các loại hình tam giác

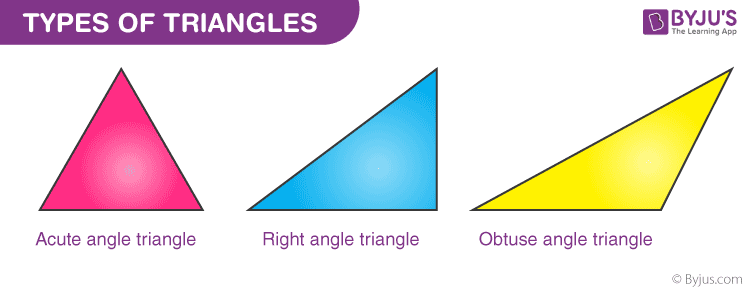
1. Tam giác nhọn:  Khi góc giữa 2 cạnh bất kỳ nhỏ hơn 90 độ thì được gọi là tam giác nhọn.
2. Tam giác vuông:  Khi góc giữa một cặp cạnh bằng 90 độ thì được gọi là tam giác vuông.
3. Tam giác góc tù: Khi góc giữa một cặp cạnh lớn hơn 90 độ thì được gọi là tam giác góc tù.

Ba loại tam giác khác dựa trên các cạnh của tam giác.

• Tam giác vô hướng (Cả ba cạnh đều không bằng nhau)
• Tam giác cân (Hai cạnh bằng nhau)
• Tam giác đều (Cả ba cạnh đều bằng nhau)

Lưu ý: Cả một tam giác vô hướng và một tam giác cân đều có thể là một tam giác vuông. Một tam giác vuông vô hướng sẽ có độ dài cả ba cạnh không bằng nhau và bất kỳ góc nào trong một góc sẽ là góc vuông. Một tam giác vuông cân sẽ có độ dài đáy và các cạnh vuông góc bằng nhau, bao gồm cả góc vuông. Cạnh không bằng thứ ba sẽ là cạnh huyền.

Tam giác góc phải

Tam giác vuông là loại tam giác có một trong các góc của nó bằng 90 độ. Hai góc còn lại tổng bằng 90 độ. Các cạnh bao gồm góc vuông là vuông góc và là đáy của tam giác. Cạnh thứ ba được gọi là cạnh huyền, là cạnh dài nhất trong cả ba cạnh. Cạnh đối diện với góc vuông là cạnh nhỏ nhất.

Ba cạnh của tam giác vuông liên hệ với nhau. Mối quan hệ này được giải thích bằng định lý Pythagoras . Theo định lý này, trong một tam giác vuông,

Hypotenuse ² = Vuông góc ² + Cơ số ²

Xem hình bên dưới để hiểu rõ hơn.

Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông nhỏ khác. Chúng ta có thể tạo ra định lý Pythagoras khi bình phương độ dài của cạnh huyền bằng tổng độ dài bình phương của cơ sở và chiều cao.

Hình dạng của tam giác phải

Tam giác vuông là một hình có ba cạnh, có một cạnh vuông góc.

Thuộc tính tam giác góc phải

Chúng ta hãy thảo luận, các tính chất của một tam giác vuông.

• Một góc luôn là 90 ° hoặc góc vuông.
•  Cạnh đối diện với góc 90 ° là cạnh huyền.
• Cạnh huyền luôn là cạnh dài nhất.
• Tổng của hai góc trong còn lại bằng 90 ° .
• Hai cạnh còn lại kề với góc vuông gọi là cạnh đáy và vuông góc.
• Diện tích của tam giác vuông bằng một nửa tích các cạnh kề của góc vuông, tức là

Diện tích Tam giác Góc vuông = ½ (Cơ sở × Vuông góc)

• Nếu chúng ta thả một góc vuông góc với cạnh huyền, chúng ta sẽ nhận được ba tam giác đồng dạng.
• Nếu ta vẽ một đường tròn ngoại tiếp đi qua cả ba đỉnh thì bán kính của đường tròn này bằng một nửa độ dài cạnh huyền.
• Nếu một trong  hai góc bằng 90 ° và hai góc còn lại mỗi góc bằng 45 °  thì tam giác đó được gọi là Tam giác vuông cân, trong đó các cạnh kề 90 °  có độ dài bằng nhau.

Trên đây là các tính chất chung của tam giác vuông. Việc dựng tam giác vuông cũng rất dễ dàng. Hãy tiếp tục học với BYJU’S để có thêm nhiều tài liệu học tập liên quan đến các chủ đề khác nhau của Hình học và các chủ đề chủ quan khác.

Diện tích tam giác vuông góc

Diện tích nằm trong vùng hai chiều và được đo bằng đơn vị hình vuông. Nó có thể được định nghĩa là lượng không gian được chiếm bởi đối tượng 2 chiều.

Diện tích của một tam giác có thể được tính bằng 2 công thức:

khu vực = a × b2

và

Công thức Heron tức là diện tích =s ( s – a ) ( s – b ) ( s – c )—————–√,

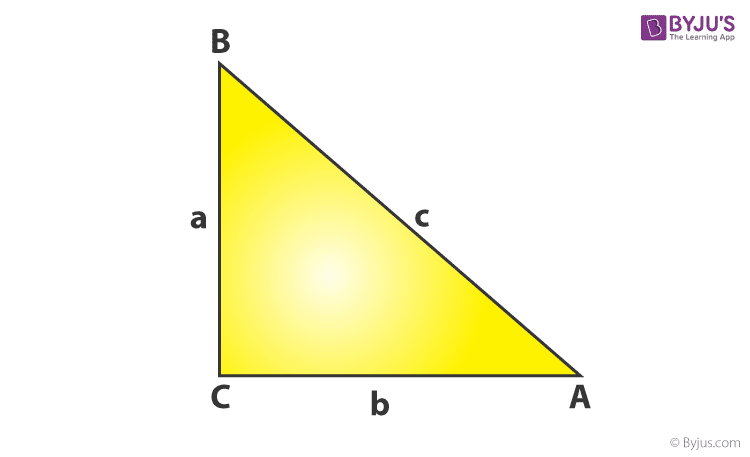
Trong đó, s là nửa chu vi và được tính bằng s =a + b + c2 và a, b, c là các cạnh của một tam giác.

Hãy để chúng tôi tính diện tích của một hình tam giác bằng cách sử dụng hình dưới đây.

Hình 1: Chúng ta hãy thả một vuông góc với cơ sở b trong tam giác đã cho.

Hình 2: Bây giờ chúng ta hãy gắn một hình tam giác khác vào một cạnh của hình tam giác. Nó tạo thành hình dạng của một hình bình hành như thể hiện trong hình.

Hình 3: Chúng ta hãy di chuyển tam giác màu đỏ sang phía bên kia của hình bình hành như trong hình trên.

Hình 4: Bây giờ nó có hình dạng của một hình chữ nhật.

Bây giờ theo tính chất của diện tích, nó được tính bằng phép nhân của hai cạnh bất kỳ

Do đó, diện tích = b × h (đối với hình chữ nhật)

Do đó, diện tích của một tam giác vuông sẽ bằng một nửa tức là

A r e a =b × h2

Cho tam giác vuông cân, đáy luôn vuông góc với chiều cao. Khi không cho trước các cạnh của tam giác và chỉ cho các góc thì diện tích của một tam giác vuông có thể được tính theo công thức:

A r e a =b c × b a2

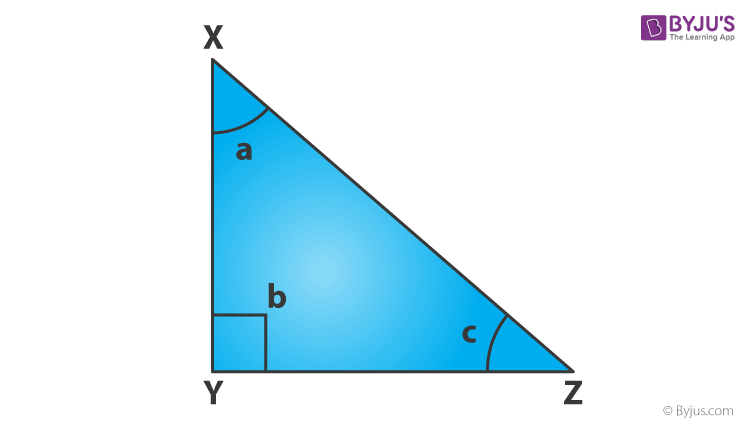
Trong đó a, b, c là các góc tương ứng của tam giác vuông, với ∠b luôn bằng 90 °.

Chu vi

Như chúng ta đã biết, ba cạnh của tam giác vuông là Cơ sở, Vuông góc và Cạnh huyền. Như vậy chu vi của tam giác vuông là tổng của cả ba cạnh của nó.

Chu vi của tam giác vuông = Chiều dài của (Cơ sở + Vuông góc + Hình tam giác)

Ví dụ: Nếu Cơ sở = 4cm, Vuông góc = 3cm và Hạ huyền = 5cm. Chu vi tam giác vuông là bao nhiêu?

Chu vi = 4 + 3 + 5 = 12 cm

Các ví dụ đã giải quyết

H.1: Trong một tam giác vuông, nếu vuông góc = 8 cm và cạnh đáy = 6 cm thì cạnh huyền có giá trị là bao nhiêu?

Giải pháp: Đưa ra,

Vuông góc = 8 cm

Cơ sở = 6cm

Chúng ta cần tìm ra cạnh huyền.

Theo định lý Pythagoras, chúng ta biết rằng;

Hypotenuse = √ (Vuông góc ² + Cơ sở ² )

H = √ (6 ² + 8 ² )

= √36 + 64

= √100

= 10 cm

Do đó cạnh huyền của tam giác vuông là 10 cm.

H.2: Nếu cạnh huyền là 13 cm và cạnh đáy là 12 cm thì tìm độ dài đường trung trực của tam giác vuông?

Giải pháp: Đưa ra,

Hypotenuse = 13 cm

Cơ sở = 12 cm

Vuông góc =?

Theo định lý Pythagoras, chúng ta biết rằng,

Hypotenuse ² = Vuông góc ² + Cơ số ²

Vuông góc ² = Hypotenuse ² – Cơ sở ²

P = √ (13 ² – 12 ² )

P = √ (169 – 144)

P = √25

P = 5 cm

Do đó, giá trị của vuông góc là 5cm.