Thừa số nguyên tố và những cách giải nhanh nhất

Nhân thừa số nguyên tố là một phương pháp tìm tất cả các số nguyên tố nhân với nhau để tạo thành một số. Thừa số là những số được nhân lên để được một số, còn thừa số nguyên tố là những số chỉ có thể chia cho 1 hoặc chính nó.

Làm thế nào để tìm thừa số nguyên tố?

Có hai phương pháp tìm thừa số nguyên tố. Đây là sự phân chia lặp lại và cây nhân tố.

Sự phân chia lặp đi lặp lại

Một số được rút gọn bằng cách chia nó một số cho các số nguyên tố. Các thừa số nguyên tố của số 36 được tìm thấy bằng phép chia lặp lại như được hiển thị:

Do đó, các thừa số nguyên tố của số 36 là 2 và 3. Điều này có thể được viết là: 2 × 2 × 3 × 3. Nên bắt đầu chia một số cho số nguyên tố nhỏ nhất và chuyển sang các thừa số lớn hơn.

ví dụ 1

Các thừa số nguyên tố của 16 là gì?

Giải pháp

Cách tốt nhất để giải loại bài toán này là xác định thừa số nguyên tố nhỏ nhất của một số, đối với trường hợp này là 2.

Số bị chia cho 16;

16 ÷ 2 = 8

Vì 8 không phải là số nguyên tố nên tiến hành chia lại cho thừa số nhỏ nhất;

8 ÷ 2 = 4

4 ÷ 2 = 2

Chúng ta có 16 thừa số nguyên tố được tô màu vàng và chúng bao gồm: 2 x 2 x 2 x 2.

có thể được viết dưới dạng số mũ:

16 = 2 ²

Ví dụ 2

Tìm các thừa số nguyên tố của 12.

Giải pháp

Chia 12 cho 2;

12 ÷ 2 = 6

6 không phải là số nguyên tố, tiến hành;

6 ÷ 2 = 3.

Do đó, 12 = 2 x 2 x 3

12 = 2 ² × 3

Cần lưu ý rằng, tất cả các thừa số nguyên tố của một số đều là số nguyên tố.

Ví dụ 3

Phân tích số 147.

Giải pháp

Bắt đầu bằng cách chia 147 cho số nguyên tố nhỏ nhất.

147 ÷ 2 = 73,5

Câu trả lời của chúng tôi không phải là số nguyên, hãy thử số nguyên tố tiếp theo là 3.

147 ÷ 3 = 49

Đúng, 3 đã thành công, bây giờ hãy chuyển sang số nguyên tố tiếp theo có thể chia 49.

49 ÷ 7 = 7

Do đó, 147 = 3 x 7 x 7,

= 3 x 7 ² .

Ví dụ 4

Số nguyên tố của 19 là bao nhiêu?

19 = 19

Giải pháp

Một phương pháp khác về cách thực hiện phân tích nhân tử là chia nhỏ một số thành hai số nguyên. Bây giờ hãy tìm các thừa số nguyên tố của các số nguyên. Kỹ thuật này rất hữu ích khi xử lý các số lớn hơn.

Ví dụ 5

Tìm các thừa số nguyên tố của 210.

Giải pháp

Chia nhỏ 210 thành:

210 = 21 x 10

Bây giờ hãy tính các thừa số của 21 và 10

21 ÷ 3 = 7

10 ÷ 2 = 5

Kết hợp các yếu tố: 210 = 2 x 3 x 5 x 7

Cây nhân tố

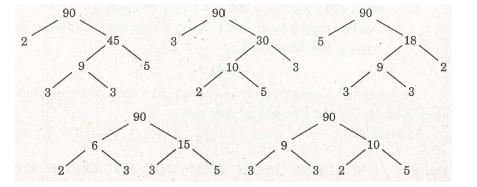
Cây thừa số liên quan đến việc tìm các thừa số nguyên tố của một số bằng cách vẽ các chương trình giống như cây. Cây thừa số là công cụ tốt nhất để tính thừa số nguyên tố. Các thừa số nguyên tố của 36 được lấy bằng cây thừa số như hình dưới đây:

Thực hành các vấn đề

1. Sau đây là các thừa số nguyên tố của một số nhất định. Tính số.

(i) 3 × 5 × 11

(ii) 2 × 5 × 7

(iii) 2 × 3 × 13

(iv) 2 × 3 × 3 × 7

(v) 3 × 7 × 11

(vi) 3 × 5 × 5

(vii) 2 × 3 × 7

(viii) 2 × 2 × 3 × 11

(ix) 3 × 7 × 11 × 11

2. Xác định số nguyên tố của các số này bằng phương pháp chia.

(i) 56

(ii) 38

(iii) 12

(iv) 120

(v) 64

(vi) 49

(vii) 81

(viii) 21

3. Sử dụng phương pháp thừa số, xác định thừa số nguyên tố của:

(i) 70

(ii) 11

(iii) 99

(iv) 44

(v) 62

(vi) 76

(vii) 97

(viii) 63

4. Xác định dữ liệu bằng bất kỳ phương pháp nào.

(i) 9

(ii) 63

(iii) 90

(iv) 48

(v) 34

(vi) 40

(vii) 66

(viii) 88

(ix) 52

(x) 98

(xi) 75

(xii) 100

5. Các thừa số nguyên tố của 19 là gì?
6. 19
   b. 0
   c. 2 x 9,5
   d. Không có cái nào ở trên
7. Các thừa số nguyên tố của 50 là gì?
8. 2 x 2 x 12,5
   b. 2 x 25
   c. 2 x 5x 5
   d. 1 x 2 x 5 x 5
9. Tính các thừa số nguyên tố của 25.
10. 2 x12,5
    b. 5 x 5
    c. 1 x 25
    d. 5 x 5,5

8 . Tìm các thừa số nguyên tố của 81.

1. 3 x 2 7
   b. 3 x 3 x 3 x3
   c. 9 x 9
   d. Không có cái nào ở trên
2. Xác định tất cả các thừa số nguyên tố của 125.
3. 1 x 125
   b. 5 x 5 x 5
   c. 2 x 5 x 12,5
   d. Tất cả những điều trên
4. Tính các thừa số nguyên tố của 132.
5. 2 x 2 x 3 x 11
   b. 2 x 6 x 11
   c.2 x 2 x 2 x 3 x 11
   d. 4 x 3 x11

Câu trả lời

1. (i) 165

(ii) 70

(iii) 78

(iv) 126

(v) 231

(vi) 75

(vii) 42

(viii) 132

(ix) 2541

1. (i) 2 ² × 7

(ii) 2 × 19

(iii) 2 × 2 x 3

(iv) 2 ³ x 3 x 5

(v) 2 ⁶

(vi) 7 x 7

(vii) 3 x 3 x 3 x 3

(viii) 3 × 7

1. (i) 2 × 5 x 7

(ii) 11

(iii) 3 x 3 x 11

(iv) 2 x 2 x 11

(v) 2 × 31

(vi) 2 × 2 × 19

(vii) 97

(viii) 3 x 3 x 7

1. (i) 3 x 3

(ii) 3 x 3 x 7

(iii) 2 x 3 x 3 x 5

(iv) 2 × 2 x 2 x 2 x 3

(v) 2 × 17

(vi) 2 × 2 × 2 x 5

(vii) 2 × 3 × 11

(viii) 2 × 2 × 2 × 11

(ix) 2 x 2 x 13

(x) 2 × 7 x 7

(xi) 3 x 5 x 5

(xii) 2 x 2 x 5 x 5

1. 1. Trả lời 19
   2. Trả lời 2 x 5 x 5
   3. Trả lời. 5 x 5
   4. Trả lời. 3 x 3 x 3 x 3
   5. Trả lời. 5 x 5 x 5
   6. Trả lời . 2 x 2 x 3 x 11

Xem thêm:

Số nguyên tố & tổng hợp – Giải thích với các ví dụ

Thứ tự hoạt động và các nguyên tắc cần nắm