Các tích phân thường được phân thành hai loại, cụ thể là:
- Tích phân xác định
- Không xác định, không thể thiếu
Ở đây, chúng ta hãy thảo luận về một trong những loại tích phân được gọi là “Tích phân không xác định” với định nghĩa và tính chất chi tiết.
Định nghĩa tích phân không xác định
Một tích phân không có bất kỳ giới hạn trên và dưới nào được gọi là một tích phân không xác định.
Về mặt toán học, nếu F (x) là một phản đạo hàm bất kỳ của f (x) thì đạo hàm tổng quát nhất của f (x) được gọi là một tích phân không xác định và được ký hiệu,
∫f (x) dx = F (x) + C
Chúng tôi đề cập bên dưới các ký hiệu / thuật ngữ / cụm từ sau với ý nghĩa của chúng trong bảng để hiểu rõ hơn.
| Ký hiệu / Điều khoản / Cụm từ | Ý nghĩa |
| ∫ f (x) dx | Tích phân của f đối với x |
| f (x) trong ∫ f (x) dx | Tích hợp |
| x trong ∫ f (x) dx | Biến số tích hợp |
| Tích phân của f | Một hàm F sao cho F ′ (x) = f (x) |
| Hội nhập | Quá trình tìm tích phân |
| Liên tục tích hợp | Bất kỳ số thực C nào, được coi là hàm hằng |
Đạo hàm chống hoặc tích phân của các hàm không phải là duy nhất. Tồn tại vô số đạo hàm của mỗi hàm số nhất định, có thể nhận được bằng cách chọn C tùy ý từ tập các số thực. Vì lý do này, C thường được gọi là một hằng số tùy ý. C là tham số mà người ta nhận được các đạo hàm (hoặc tích phân) khác nhau của hàm đã cho.
Thuộc tính vô thời hạn
Bây giờ chúng ta hãy xem xét một số tính chất của tích phân bất định.
Tính chất 1: Quá trình phân hóa và tích hợp là nghịch đảo của nhau theo nghĩa của các kết quả sau:


Và


trong đó C là hằng số bất kỳ.
Bây giờ chúng ta hãy chứng minh tuyên bố này.
Chứng minh: Xét một hàm f sao cho phản đạo hàm của nó được cho bởi F, tức là


Sau đó,
![]()
![]()
Khi phân biệt cả hai bên đối với x, chúng ta có


Như chúng ta đã biết, đạo hàm của bất kỳ hàm hằng số nào đều bằng không. Vì vậy,


Đạo hàm của hàm số f theo x được cho là f ‘(x), do đó ta nhận được;


Vì thế,


Do đó, đã chứng minh.
Tính chất 2: Hai tích phân bất định có cùng đạo hàm dẫn đến cùng một họ đường cong, và do đó chúng tương đương.
Chứng minh: Cho f và g là hai hàm sao cho


Hiện nay,


trong đó C là bất kỳ số thực nào.
Từ phương trình này, chúng ta có thể nói rằng họ các đường cong của [∫ f (x) dx + C 3 , C 3 ∈ R] và [∫ g (x) dx + C 2 , C 2 ∈ R] là như nhau .
Do đó, chúng ta nói rằng, ∫ f (x) dx = ∫ g (x) dx
Tính chất 3: Tích phân của tổng hai hàm số bằng tổng tích phân của các hàm đã cho, tức là


Bằng chứng:
Từ tính chất 1 của tích phân, chúng ta có


Ngoài ra, chúng ta có thể viết;


Từ (1) và (2),


Do đó đã chứng minh.
Tính chất 4: Với bất kỳ giá trị thực nào của p,
![]()
![]()
Chứng minh: Từ tính chất 1, chúng ta có thể nói rằng
![]()
![]()
Cũng thế,
![]()
![]()
Từ thuộc tính 2, chúng ta có thể nói rằng
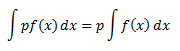
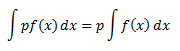
Thuộc tính 5:
Đối với một số hữu hạn các hàm f 1 , f 2 …. f n và các số thực p 1 , p 2 … p n ,
∫ [p 1 f 1 (x) + p 2 f 2 (x)…. + P n f n (x)] dx = p 1 ∫f 1 (x) dx + p 2 ∫f 2 (x) dx + … .. + p n ∫f n (x) dx
Công thức tích phân không xác định
Danh sách các công thức tích phân không xác định là
- ∫ 1 dx = x + C
- ∫ a dx = ax + C
- ∫ x n dx = ((x n + 1 ) / (n + 1)) + C; n ≠ 1
- ∫ sin x dx = – cos x + C
- ∫ cos x dx = sin x + C
- ∫ giây 2 x dx = tan x + C
- ∫ cosec 2 x dx = -cot x + C
- ∫ giây x tan x dx = giây x + C
- ∫ cosec x cot x dx = -cosec x + C
- ∫ (1 / x) dx = ln | x | + C
- ∫ e x dx = e x + C
- ∫ a x dx = (a x / ln a) + C; a> 0, a ≠ 1
Ví dụ về tích phân không xác định
Xem qua các ví dụ và giải pháp tích phân không xác định sau được đưa ra dưới đây:
Ví dụ 1:
Đánh giá bài toán tích phân không xác định đã cho: ∫6x 5 -18x 2 +7 dx
Giải pháp:
Được,
∫6x 5 -18x 2 +7 dx
Tích hợp hàm đã cho, nó trở thành:
∫6x 5 -18x 2 +7 dx = 6 (x 6 /6) – 18 (x 3 /3) + 7x + C
Lưu ý: Đừng quên đặt hằng số tích hợp “C”
Sau khi đơn giản hóa, chúng tôi nhận được giải pháp
Do đó, ∫6x 5 -18x 2 +7 dx = x 6 -6x 3 + 7x + C
Ví dụ 2:
Đánh giá f (x), cho rằng f ‘(x) = 6x 8 -20x 4 + x 2 + 9
Giải pháp:
Được,
f ‘(x) = 6x 8 -20x 4 + x 2 + 9
Chúng ta biết rằng, quá trình nghịch đảo của sự khác biệt là một quá trình tích hợp.
Do đó, f (x) = ∫f ‘(x) dx = ∫ [6x 8 -20x 4 + x 2 + 9] dx
f (x) = (2/3) x 9 – 4x 5 + (1/3) x 3 + 9x + C
Tích phân không xác định so với Tích phân xác định
Một tích phân không xác định là một hàm thực hành lấy đạo hàm của một hàm khác. Nó có thể được biểu diễn một cách trực quan dưới dạng một ký hiệu tích phân, một hàm, và sau đó là một dx ở cuối. Các thể thiếu không xác định là một cách dễ dàng hơn để biểu thị nhận được nguyên hàm. Tích phân không xác định tương tự như tích phân xác định, nhưng cả hai không giống nhau. Hình dưới đây cho thấy sự khác biệt giữa tích phân xác định và tích phân không xác định.


Câu hỏi thường gặp – Câu hỏi thường gặp
Làm thế nào để bạn tìm thấy tích phân bất định?
∫f (x) dx = F (x) + C, trong đó C là số thực bất kỳ.
Thông thường, chúng tôi sử dụng các công thức phù hợp để giúp lấy được hàm khử của hàm đã cho.
Kết quả của tích phân bất định là một hàm.