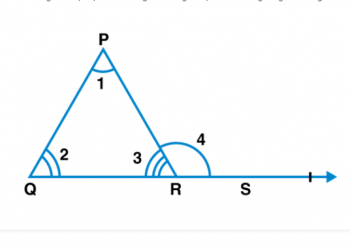
Xem xét miền và phạm vi của các hàm nghịch đảo, cần lưu ý các công thức sau:
- sin (sin −1 x) = x, nếu -1 ≤ x ≤ 1
- cos (cos −1 x) = x, nếu -1 ≤ x ≤ 1
- tan (tan −1 x) = x, nếu -∞ ≤ x ≤∞
- cot (cot −1 x) = x, nếu -∞≤ x ≤∞
- sec (sec −1 x) = x, nếu -∞ ≤ x ≤ -1 hoặc 1 ≤ x ≤ ∞
- cosec (cosec −1 x) = x, nếu -∞ ≤ x ≤ -1 hoặc 1 ≤ x ≤ ∞
Ngoài ra, các công thức sau đây được xác định cho các hàm lượng giác nghịch đảo.
- sin −1 (sin y) = y, nếu -π / 2 ≤ y ≤ π / 2
- cos −1 (cos y) = y, nếu 0 ≤ y ≤ π
- tan −1 (tan y) = y, nếu -π / 2 <y <π / 2
- cot −1 (cot y) = y nếu 0 <y <π
- sec −1 (sec y) = y, nếu 0 ≤ y ≤ π, y ≠ π / 2
- cosec −1 (cosec y) = y nếu -π / 2 ≤ y ≤ π / 2, y ≠ 0
Các tính chất quan trọng của hàm lượng giác nghịch đảo
Dưới đây là một số tính chất quan trọng liên quan đến các hàm lượng giác nghịch đảo:
Bộ thuộc tính 1:
- Sin −1 (x) = cosec −1 (1 / x), x∈ [−1,1] – {0}
- Cos −1 (x) = sec −1 (1 / x), x ∈ [−1,1] – {0}
- Tan −1 (x) = cot −1 (1 / x), nếu x> 0 (hoặc) cot −1 (1 / x) −π, nếu x <0
- Cót −1 (x) = tan −1 (1 / x), nếu x> 0 (hoặc) tan −1 (1 / x) + π, nếu x <0
Bộ thuộc tính 2:
- Sin −1 (−x) = −Sin −1 (x)
- Tan −1 (−x) = −Tan −1 (x)
- Cos −1 (−x) = π – Cos −1 (x)
- Cosec −1 (−x) = – Cosec −1 (x)
- Sec −1 (−x) = π – Sec −1 (x)
- Cot −1 (−x) = π – Cot −1 (x)
Bằng chứng:
1. Sin −1 (−x) = −Sin −1 (x)
Cho sin −1 (−x) = y, tức là, −x = sin y
⇒ x = – sin y
Vì vậy,
x = sin (- y)
Hoặc là,
sin −1 (x) = −y = −sin −1 (−x)
Do đó, sin −1 (−x) = −sin −1 (x)
Tương tự, sử dụng cùng một khái niệm có thể thu được các kết quả sau:
- cosec −1 (−x) = −cosec −1 x, | x | ≥1
- tan −1 (−x) = −tan −1 x, xϵR
2. Cos −1 (−x) = π – Cos −1 (x)
Đặt cos −1 (−x) = y tức là −x = cos y
⇒ x = −cos y = cos (π – y)
Vì vậy,
cos −1 (x) = π – y
Hoặc là,
cos −1 (x) = π – cos −1 (−x)
Do đó, cos −1 (−x) = π – cos −1 (x)
Tương tự, sử dụng cùng một khái niệm có thể thu được các kết quả sau:
- sec −1 (−x) = π – sec −1 x, | x | ≥1
- cot −1 (−x) = π – cot −1 x, xϵR
Bộ thuộc tính 3:
- Sin −1 (1 / x) = cosec −1 x, x≥1 hoặc x≤ − 1
- Cos −1 (1 / x) = sec −1 x, x≥1 hoặc x≤ − 1
- Tan −1 (1 / x) = −π + cot −1 (x)
Chứng minh: Sin −1 (1 / x) = cosec −1 x, x≥1 hoặc x≤ − 1
Cho cosec −1 x = y, tức là x = cosec y
⇒ (1 / x) = sin y
Do đó, sin −1 (1 / x) = y
Hoặc là,
sin −1 (1 / x) = cosec −1 x
Tương tự, sử dụng cùng một khái niệm, các kết quả khác có thể thu được.
Hình ảnh minh họa:
- sin −1 (⅓) = cosec −1 (3)
- cos −1 (¼) = giây −1 (4)
- sin −1 (−¾) = cosec −1 (−4/3) = sin −1 (3/4)
- tan −1 (−3) = cot −1 (−⅓) −π
Bộ thuộc tính 4:
- Sin −1 (cos θ) = π / 2 – θ, nếu θ∈ [0, π]
- Cos −1 (sin θ) = π / 2 – θ, nếu θ∈ [−π / 2, π / 2]
- Tan −1 (cot θ) = π / 2 – θ, θ∈ [0, π]
- Cot −1 (tan θ) = π / 2 – θ, θ∈ [−π / 2, π / 2]
- Sec −1 (cosec θ) = π / 2 – θ, θ∈ [−π / 2, 0] ∪ [0, π / 2]
- Cosec −1 (giây θ) = π / 2 – θ, θ∈ [0, π] – {π / 2}
- Sin −1 (x) = cos −1 [√ (1 − x 2 )], 0≤x≤1
= −cos −1 [√ (1 − x 2 )], −1≤x <0
Hình ảnh minh họa:
1. Cho, cos −1 (−3/4) = π – sin −1 A. Tìm A.
Giải pháp:
Vẽ sơ đồ từ câu hỏi.


Vì thế,
cos −1 (−3/4) = π – sin −1 (√7 / 4)
Do đó, A = √7 / 4
2. cos −1 (¼) = sin −1 √ (1−1 / 16) = sin −1 (√15 / 4)
3. sin −1 (−½) = −cos −1 √ (1 – ¼) = −cos −1 (√3 / 2)
4. sin 2 (tan −1 (¾)) = sin 2 (sin −1 (⅗)) = (⅗) 2 = 9/25.
5. sin −1 (sin 2π / 3) = π / 3
6. cos −1 (cos 4π / 3) = 2π / 3
7. sin −1 (cos 33π / 10) = sin −1 cos (3π + 3π / 10) = sin −1 (insin (π / 2 – 3π / 10)) = – (π / 2 – 3π / 10) = −π / 5
Bộ thuộc tính 5:
- Sin −1 x + Cos −1 x = π / 2
- Tan −1 x + Cot −1 (x) = π / 2
- Sec −1 x + Cosec −1 x = π / 2
Chứng minh: sin −1 (x) + cos −1 (x) = (π / 2), xϵ [−1,1]
Cho sin −1 (x) = y, tức là x = sin y = cos ((π / 2) – y)
⇒ cos −1 (x) = (π / 2) – y = (π / 2) – sin −1 (x)
Vì vậy,
sin −1 (x) + cos −1 (x) = (π / 2)
Tương tự, sử dụng cùng một khái niệm có thể thu được các kết quả sau:
- tan −1 (x) + cot −1 (x) = (π / 2), xϵR
- cosec −1 (x) + sec −1 (x) = (π / 2), | x | ≥1
Hình ảnh minh họa:
1. Sec −1 (4) + Cosec −1 (4) = π / 2
2. Tan −1 (3) + Cot −1 (3) = π / 2
Bộ thuộc tính 6:
(1) Nếu x, y> 0
Tan −1 x + Tan −1 y =⎧⎩⎨⎪⎪rám nắng– 1(x + y1 – x y) xy< 1Số Pi+rám nắng– 1(x + y1 – x y) xy> 1
(2) Nếu x, y <0
Tan −1 x + Tan −1 y =⎧⎩⎨⎪⎪rám nắng– 1(x + y1 – x y) xy< 1– π+rám nắng– 1(x + y1 – x y) xy< 1
(3) Tan −1 x + Tan −1 y =rám nắng– 1(x – y1 + x y) xy =Số Pi+rám nắng– 1(x – y1 + x y)x > 0Y< 0 = – π+rám nắng– 1(x – y1 + x y)x < 0Y> 0
(4) tan −1 (x) – tan −1 (y) = tan −1 [(x – y) / (1 + xy)], xy> −1
(5) 2tan −1 (x) = tan −1 [(2x) / (1 – x 2 )], | x | <1
Chứng minh: Tan −1 (x) + tan −1 (y) = tan −1 [(x + y) / (1 – xy)], xy <1
Cho tan −1 (x) = α và tan −1 (y) = β, tức là, x = tan (α) và y = tan (β)
⇒ tan (α + β) = (tan α + tan β) / (1 – tan α tan β)
Vì vậy,
(α) + (β) = tan −1 [(x + y) / (1 – xy)]
Vì thế,
tan −1 (x) + tan −1 (y) = tan −1 [(x + y) / (1 – xy)]
Tương tự, sử dụng cùng một khái niệm có thể thu được các kết quả sau:
- tan −1 (x) – tan −1 (y) = tan −1 [(x – y) / (1 + xy)], xy> −1
- 2tan −1 (x) = tan −1 [(2x) / (1 – x 2 )], | x | <1
Hình ảnh minh họa:
1. Tan −1 (−½) + Tan −1 (−⅓) = Tan −1 [(−½ – ⅓) / (1− ⅙)]
= tan −1 (−1)
−π / 4
2. Tan −1 (−2) + Tan −1 (−3) = Tan −1 [(−2 + −3) / (1−6)]
= Tan −1 (−5 / −5) = Tan −1 1
= π / 4
3. Tan −1 (−3) + Tan −1 (−⅓) = – (Tan −1 B) + Tan −1 (⅓)
−π / 2
4. Tan −1 (5/3) – Tan −1 (¼) = Tan −1 [ (5/3 – ¼) / (1 + 5/12)]
= Tan −1 (17/17)
= Tan −1 1 = π / 4
5. Tan −1 2x + Tan −1 3x = π / 4
⇒ Tan −1 [(5x) / (1−6x 2 )] = π / 4
⇒ 5x / (1−6x 2 ) = 1
⇒ 6x 2 – 5x + 1 = 0
⇒ x = 1/6 hoặc −1
∴ x = 16 như, x = −1
6. Nếu tan −1 (4) + Tan −1 (5) = Cot −1 (λ). Tìm λ
Đây,
Tan −1 [9 / (1−20)] = Cot −1 λ
⇒ Tan −1 (-9/19) = Cot −1 (λ)
An −Tan −1 (9/19) = Cot −1 (λ)
⇒ −Cot −1 (19/9) = Cot −1 (λ)
Hoặc, λ = −19/9
Bộ thuộc tính 7:
- sin −1 (x) + sin −1 (y) = sin −1 [x√ (1 – y 2 ) + y√ (1 – x 2 )]
- cos −1 x + cos −1 y = cos −1 [xy − √ (1 − x 2 ) √ (1 − y 2 )]
Hình minh họa:
1. sin −1 (⅘) + sin −1 (7/25) = sin −1 (A). Tìm một.
Giải pháp:
= sin −1 (⅘ √ {1− (7/25) 2 } + √ {1− (⅘) 2 } 7/25)
= sin −1 (117/125)
2. Chứng minh rằng sin −1 (⅘) + sin (5/13) + sin −1 (16/65) = π / 2
Giải pháp:
sin −1 (63/65) + sin −1 (16/65)
= cos −1 (16/65) + sin −1 (16/65)
= π / 2
Bộ thuộc tính 8: Đồ thị tương ứng
- sin −1 (sin x) = −π – π, nếu x∈ [−3π / 2, −π / 2]
= x, nếu x∈ [−π / 2, π / 2]
= π – x, nếu x∈ [π / 2, 3π / 2]
= −2π + x, nếu x∈ [3π / 2, 5π / 2] Và như vậy.


- cos −1 (cos x) = 2π + x, nếu x∈ [−2π, −π]
= −x, ∈ [−π, 0]
= x, ∈ [0, π]
= 2π – x, ∈ [π, 2π]
= −2π + x, ∈ [2π, 3π]


- tan −1 (tan x) = π + x, x∈ (−3π / 2, −π / 2)
= x, (−π / 2, π / 2)
= x – π, (π / 2, 3π / 2)
= x − 2π, (3π / 2, 5π / 2)


Hình minh họa:
1. sin −1 (sin 2π / 3) = π – 2π / 3 = π / 3
2. cos −1 (cos (13π / 6)) = π / 6
3. sin −1 sin (4) = π – 4
4. sin −1 sin (6) = 6−2π
5. sin −1 sin (12) = 12−4π
6. cos −1 (cos 3) = 3
7. cos −1 (cos 5) = 2π – 5
8. cos −1 (cos 6) = 2π – 6
9. tan −1 (tan 3) = 3 − π
Bộ thuộc tính 9:
1. 2không có– 1x =không có– 1( 2 x1 –x2—–√)
2. 2cos– 1x =cos– 1( 2x2– 1 )
3. 2rám nắng– 1x =không có– 1(2 x1 +x2)
4. cos– 1(1 –x21 +x2) =2rám nắng– 1x
5. 3không có– 1x =không có– 1( 3 x – 4x3)
6. 3cos– 1x =cos– 1( 4x3– 3 x )
7. 3rám nắng– 1x =rám nắng– 1(3 x –x31 – 3x2)
số 8. 2rám nắng– 1x =rám nắng– 1(2 x1 –x2)
Hình ảnh minh họa:
1. f (x) = không có– 1(2 x1 +x2) +2rám nắng– 1x .
Nếu x> 1 tìm được cos (f (10))
Nhiều năm. f( 10 ) = s tôin– 1(20101) +2rám nắng– 1( 10 ) =rám nắng– 1(2099) +2rám nắng– 1( 10 ) = π+rám nắng– 1(2099) ±rám nắng– 1(2099)
= π
2. Tìm rám nắng(cos– 1(45) +rám nắng– 1(23) ) = tan(rám nắng– 1(34) +rám nắng– 1(23) )
=3/4+2/31 – (34×2/3) =176
Chứng minh: 2tan −1 x = sin −1 [(2x) / (1 + x 2 )], | x | <1
Cho, tan −1 x = y tức là, x = tan y
⇒ sin −1 [(2x) / (1 + x 2 )] = sin −1 [(2tany) / (1 + tan 2 y)]
Vì vậy,
-Sin -1 [(2tany) / (1 + tan 2 y)] = sin -1 (sin2y) = 2y = 2tan -1 x
Tương tự, sử dụng cùng một khái niệm có thể kết luận các kết quả sau:
- 2tan −1 x = cos −1 [(1 – x 2 ) / (1 + x 2 ), x≥0
- 2tan −1 x = tan −1 [(2x) / (1 – x 2 ), −1 <x <1