Phép trừ các số mũ dễ hiểu, giải nhanh nhất 2021

Số mũ là lũy thừa hoặc chỉ số. Một biểu thức mũ bao gồm hai phần, đó là cơ số, được ký hiệu là b và số mũ, được ký hiệu là n. Dạng tổng quát của biểu thức mũ là b ⁿ .

Làm thế nào để Trừ số mũ?

Hoạt động trừ số mũ là khá dễ dàng nếu bạn đã hiểu rõ về số mũ. Trong bài này, bạn sẽ học các quy tắc và cách áp dụng chúng khi bạn cần trừ với số mũ.

Nhưng trước khi bắt tay vào phép trừ với số mũ, chúng ta hãy nhắc nhở bản thân một số thuật ngữ cơ bản về số mũ.

Vâng, một số mũ hoặc lũy thừa biểu thị số lần một số được nhân nhiều lần với chính nó. Ví dụ, khi chúng ta gặp một số được viết là, 5 ³ , nó chỉ đơn giản ngụ ý rằng 5 được nhân với chính nó ba lần. Nói cách khác, 5 ³ = 5 x 5 x 5 = 125

Định dạng viết số mũ tương tự cũng được áp dụng với các biến. Các biến được biểu diễn bằng chữ cái và ký hiệu. Ví dụ, khi x được nhân với chính nó 3 lần, thì chúng ta viết như sau; x ³ . Các biến thường được kèm theo hệ số. Do đó, một hệ số là một số nguyên được nhân với biến.

Ví dụ, trong 2x ³ , hệ số là số 2 và x là biến. Khi một biến không có số trước nó, hệ số luôn là 1. Điều này cũng đúng khi một số không có số mũ. Hệ số 1 thường không đáng kể, và do đó không thể viết bằng một biến.

Phép trừ số mũ thực sự không liên quan đến bất kỳ quy tắc nào. Nếu một số được nâng lên thành lũy thừa. Bạn chỉ cần tính toán kết quả và sau đó thực hiện phép trừ thông thường. Nếu cả số mũ và cơ số đều giống nhau, bạn có thể trừ chúng giống như bất kỳ số nào khác như các số hạng trong đại số. Ví dụ, 3 ^y  – 2x ^y  = x ^y .

Trừ các số mũ cùng cơ số

Hãy giải thích khái niệm này với sự trợ giúp của một vài ví dụ.

ví dụ 1

• 2 ³– 2 ² = 8 – 4 = 4
• 5 ³– 5 ² = 75 – 25 = 50
• Trừ x ³y ^{3 cho} 10 x ³ y ³

Trong trường hợp này, hệ số của số mũ là 10 và 1

Các biến giống như các điều khoản và do đó có thể được trừ

Trừ các hệ số = 10 – 1

= 9

Như vậy, 10x ³ y ³ – x ³ y ³ = 9 (xy) ³

Bạn có thể nhận thấy rằng, phép trừ các số mũ với các số hạng tương tự được thực hiện bằng cách tìm sự khác biệt của các hệ số của chúng.

• Trừ 8x ²– 4x ²

Trong trường hợp này, các biến 4x ² và 8x ² giống như các số hạng và hệ số của chúng tương ứng là 4 và 8.

= 8x ² – 4x ²

= (8-4) x ² .

= 4 x ²

• Tập luyện (-7x) – (-3x)

Ở đây, -7x và -3x giống như các thuật ngữ

= -7x – (-3x)

= -7x + 3x,

= -4x.

• 15x – 4x – 12y – 3y

Trừ các điều khoản like

15x – 4x = 11x

12y – 3y = 9y

Do đó, câu trả lời là 11x – 9y.

• Trừ (4x + 3y + z) – (2x + 3y – z).

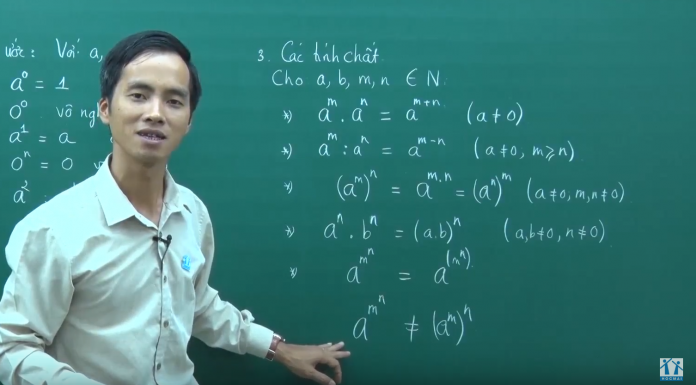
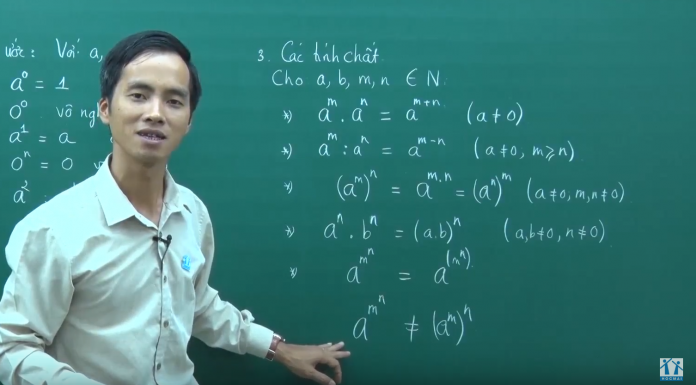
Các biến này giống như các điều khoản

(2x + 3y – z) – (4x + 3y + z)

Mở ngoặc đơn;

= 2x + 3y – z – 4x – 3y – z,

Sắp xếp lại các điều khoản tương tự và thực hiện phép trừ

= 2x – 4x + 3y – 3y – z – z

= -2x + 0 – 2z,

= -2x – 2z

Xem thêm:

Cách tính số mũ phủ định dễ như chưa từng có

Bí quyết thêm số mũ hiệu quả nhanh chóng nhất

Trừ các số mũ với cơ số khác nhau

Số mũ với các cơ số khác nhau được tính toán tách biệt và kết quả bị trừ. Mặt khác, biến có cơ số không giống nhau hoàn toàn không thể bị trừ. Ví dụ, không thể thực hiện phép trừ a và b và kết quả chỉ là a -b.

Để trừ số mũ dương m và số mũ âm n, ta chỉ cần nối cả hai số hạng bằng cách đổi dấu trừ thành dấu dương và viết kết quả dưới dạng m + n.

Do đó, phép trừ dương và âm không giống như số mũ m và -n = m + n.

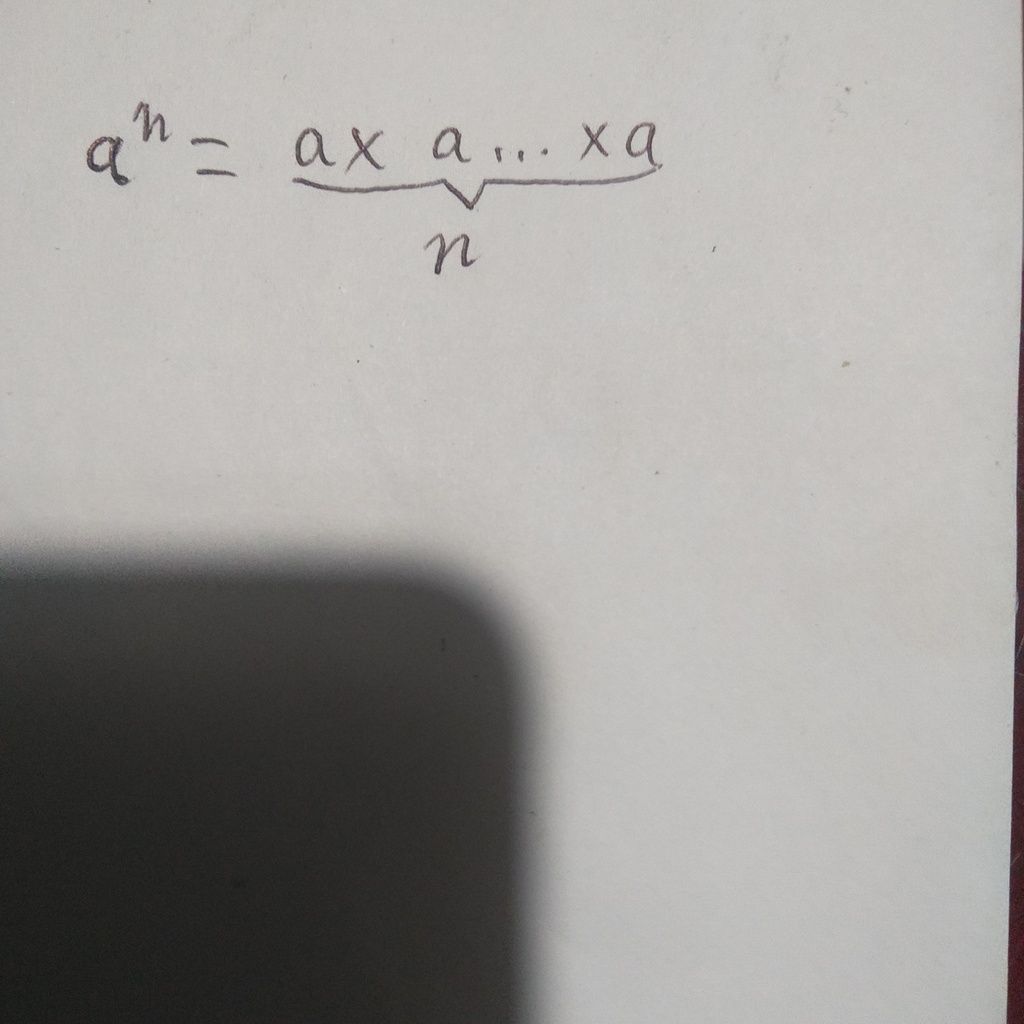
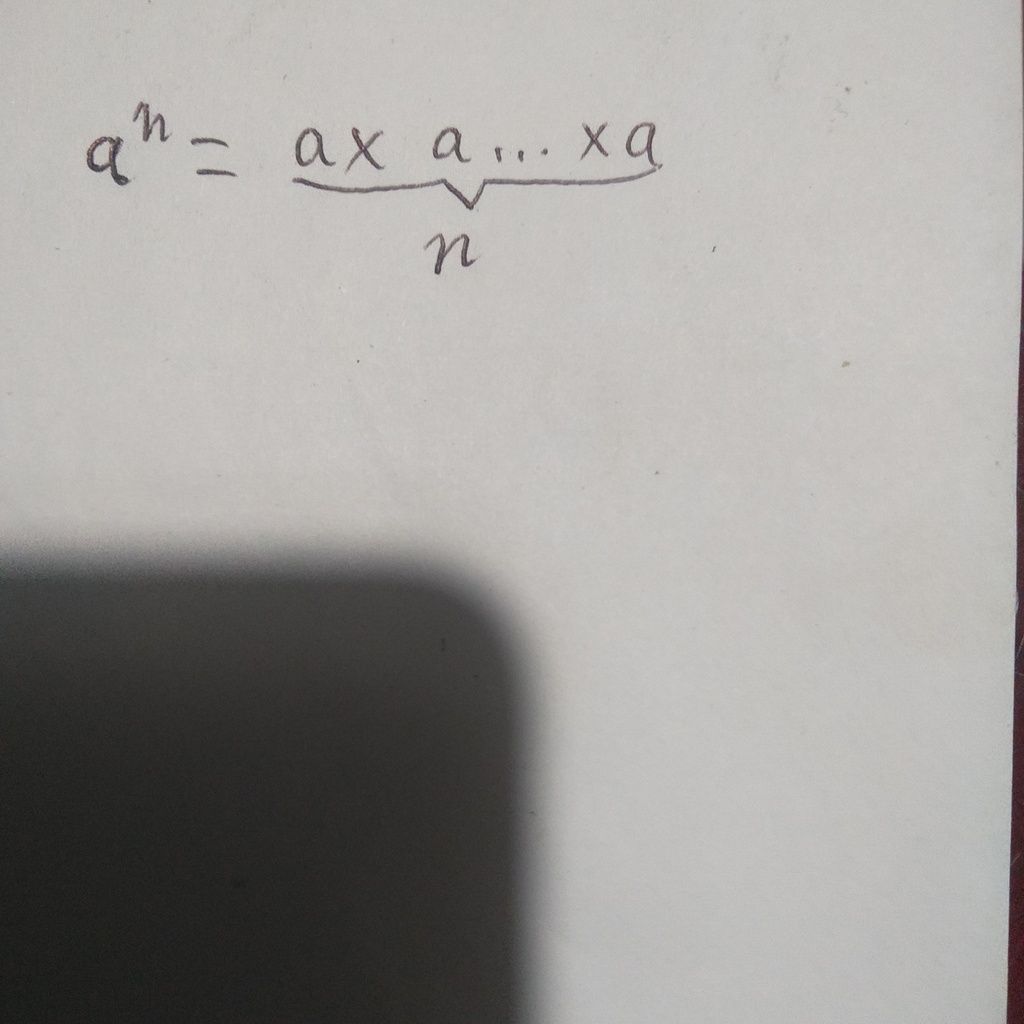
Ví dụ 2

• 4 ²– 3 ² = 16 – 9 = 7
• Trừ: 11x – 7y -2x – 3x.
  = 11x – 2x – 3x – 7y.
  = 6x – 7y
• Đánh giá 3x ²– 7y ²
  Trong trường hợp này, hai số mũ 3x ² và 7y ² không giống số hạng và do đó nó sẽ không đổi.
  Ở đây 3x và 7y cả hai đều không giống như các điều khoản nên nó sẽ vẫn như vậy.
  Do đó, câu trả lời là 3x ² – 7y ²
• Đánh giá 15x – 12y – 11x
  = 15x ⁵– 11x ⁵ – 12y ⁵
  = 4x ⁵ – 12y ⁵