Vị trí tương đối của hai đường thẳng
12 Tháng Mười Một, 2021Vị trí tương đối của hai đường thẳng là gì? Kiến thức nên nắm gồm những gì thì tintuctuyensinh...
Vectơ rất hữu ích trong cuộc sống hàng ngày. Tuy nhiên, trong thế giới thực, mọi thứ diễn ra trong không gian ba chiều. Nói chung, chúng ta học cách giải các vectơ trong không gian hai chiều. Tuy nhiên, để mở rộng và phát triển việc sử dụng vectơ trong các ứng dụng thực tế hơn, điều cần thiết là phải giải thích các vectơ dưới dạng mặt phẳng ba chiều.
Một vector 3-D được định nghĩa là:
“Vectơ ba chiều là một đoạn thẳng được vẽ trong mặt phẳng 3-D có điểm ban đầu được gọi là đuôi và điểm cuối cùng được gọi là đầu. Giống như vectơ pháp tuyến trong mặt phẳng 2-D, vectơ 3-D cũng có độ lớn và hướng ”.
Trong chủ đề này, chúng ta sẽ thảo luận chi tiết các điểm sau:
Contents
Vectơ 3-D là vectơ được biểu diễn trong mặt phẳng 3-D có ba tọa độ; x, y và z.
Như các phần trước, chúng ta đã cùng nhau tìm hiểu và thảo luận về vectơ trong không gian 2 chiều. Để tránh sự phức tạp trong tính toán và đơn giản hóa ý tưởng để chúng ta có thể hiểu khái niệm dễ dàng, đã đến lúc tìm hiểu về vectơ 3-D.
Ví dụ, nếu chúng ta cần chỉ định hướng của bất kỳ vật thể hoặc cơ thể cứng nhắc nào như ô tô, máy bay, rô bốt, v.v., người ta thường nghĩ rằng anh ta cần ba tọa độ để xác định vị trí của các đối tượng x, y và z- trục và điều đó là hoàn toàn chính xác. Vì vậy, để mô tả tác động của tất cả các tính năng, chúng ta cần sử dụng không gian ba chiều.
Tương tự, nếu chúng ta xem xét một bản đồ ở dạng 2-D, nó chỉ hữu ích cho việc điều hướng từ điểm này đến điểm khác. Tuy nhiên, nếu chúng ta cần xác định các cảnh quan và môi trường khác nhau, chỉ mô tả 2-D của bản đồ là không đủ. Đó là lý do tại sao cần phải hiểu khái niệm vectơ 3-D trong hệ tọa độ 3-D và các tính chất của chúng.
Vectơ 3-D giống như vectơ 2-D về mọi mặt, nhưng trong trường hợp của vectơ 3-D, chúng ta cần theo dõi thêm một hướng. Các phép toán vectơ 3-D tương tự như các phép toán 2-D chỉ với một bước tính toán bổ sung. Chúng ta có thể thực hiện các phép tính khác nhau như tìm góc giữa hai vectơ, phép nhân vô hướng, v.v.
Bây giờ, câu hỏi đầu tiên là, “Hệ tọa độ 3-D là gì?” Hệ tọa độ 3-D có 3 chiều hoặc có thể được coi là có 3 trục vuông góc: trục x, y và z. Hệ như vậy được gọi là hệ tọa độ hình chữ nhật 3 chiều.
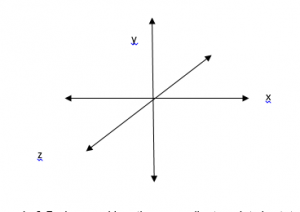

Một vectơ vẽ trong mặt phẳng 3-D và có ba điểm tọa độ được phát biểu là một vectơ 3-D. Bây giờ có ba trục, vì vậy điều này có nghĩa là có ba cặp trục giao nhau. Mỗi cặp tạo thành một mặt phẳng, mặt phẳng xy, mặt phẳng yz và mặt phẳng xz. Vectơ 3-D có thể được biểu diễn dưới dạng u (u x , u y , u z ) hoặc <x, y, z> hoặc u x i + u y j + u z k .
Độ lớn của vectơ 3-D được tính theo cách tương tự với việc bổ sung thêm một tọa độ.
| u | = √ ((u x ) ^ 2 + (u y ) ^ 2 + (u z ) ^ 2 )
Trong đó u x , u y và u z là độ lớn của các trục tọa độ.
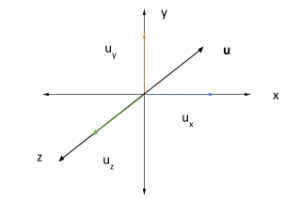

Như chúng ta đã thảo luận, khái niệm vectơ 3-D không khác với vectơ 2-D, ngoại trừ bây giờ có thêm một chiều trong vectơ 3-D. Độ lớn của một vectơ luôn luôn dương, vì sai lầm phổ biến khi tính độ lớn của một vectơ là chúng ta quên dấu tuyệt đối. Chỉ có độ lớn của vectơ null bằng không.
Hãy để chúng tôi hiểu rõ hơn về khái niệm này với sự trợ giúp của một ví dụ.
ví dụ 1
Tính độ lớn của các vectơ 3-D sau đây.
Giải pháp
Đầu tiên chúng ta hãy xem xét phương trình 1:
u = (3,4,5)
| u | = √ ((3) 2 + (4) 2 + (5) 2 )
| u | = √ (9 + 16 + 25)
| u | = 7,07
Bây giờ, hãy xem xét phương trình 2:
v = <2,5,6,>
| v | = √ ((2) 2 + (5) 2 + (6) 2 )
| v | = √ (4 + 25 + 36)
| v | = 8.06
Hãy đánh giá phương trình 3:
| s | = √ ((3) 2 + (0) 2 + (8) 2 )
| s | = √ (9 + 0 + 64)
| s | = 9,05
Vì vậy, trong các ví dụ trên, chúng ta đã tính toán độ lớn của vectơ 3-D.
Vectơ độ dời được định nghĩa là:
“ Một vectơ giải thích về sự thay đổi vị trí của vật thể được gọi là vectơ độ dời.”
Chúng ta hãy xem xét một vectơ AB có điểm đầu là A (x 1 , y 1 , z 1 ) và điểm cuối là B (x 2 , y 2 , z 2 ). Nó có một số độ lớn và hướng, và trong trường hợp này, hướng được xác định là từ A đến B.
Tọa độ của vectơ độ dời là
AB = (x 2 – x 1 , y 2 – y 1 , z 2 – z 1 )
Do đó , độ lớn được cho là:
| AB | = √ ((x 2 – x 1 ) ^ 2 + (y 2 – y 1 ) ^ 2 + (z 2 – z 1 ) ^ 2 )
Hãy tiến hành một số ví dụ.
Ví dụ 2
Cho biết tọa độ của hai điểm là A (4,6,8) và B (7,8,4). Tìm khoảng cách giữa hai điểm.
Giải pháp
Để tìm khoảng cách giữa hai điểm trong mặt phẳng 3 chiều, chúng ta sẽ sử dụng công thức sau:
| AB | = √ ((x 2 – x 1 ) ^ 2 + (y 2 – y 1 ) ^ 2 + (z 2 – z 1 ) ^ 2 )
| AB | = √ ((7 – 4) ^ 2 + (8 – 6) ^ 2 + (4 – 8) ^ 2 )
| AB | = √ ((3) ^ 2 + (2) ^ 2 + (-4) ^ 2 )
| AB | = √ (9 + 4 + 16)
| AB | = √ (29)
| AB | = 5,38
Khoảng cách giữa hai điểm là 5,38 m.
Vectơ đơn vị được định nghĩa là một loại vectơ có độ lớn luôn bằng 1. Vì vậy, vectơ đơn vị mô tả hướng của vectơ v cho rằng độ lớn của vectơ là | v |.
Sau đó, vectơ hướng được cho là,
Û = Ư / | U |
Hãy giải một số ví dụ để bao hàm khái niệm này trên vectơ 3-D.
Ví dụ 3
Tìm phương và độ lớn của vectơ 3-D PQ (3,5,6) đã cho.
Giải pháp
Độ lớn của vectơ đã cho là:
| PQ | = √ ((3) 2 + (5) 2 + (6) 2 )
| PQ | = √ (9 + 25 + 36)
| PQ | = 8,366
Hướng của vectơ 3-D được cho bởi vectơ đơn vị như sau:
U PQ = PQ / | PQ |
U PQ = [3, 5, 6] / 8.366
Ví dụ 4
Tìm phương và độ lớn của vectơ đã cho AB = 5 i + 3 j + 2 k
Giải pháp
Độ lớn của vectơ đã cho là:
| AB | = √ ((5) ^ 2 + (3) ^ 2 + (2) ^ 2 )
| AB | = √ (25 + 9 + 4)
| AB | = 6.166
Hướng của vectơ được cho bởi vectơ đơn vị như sau:
U AB = AB / | AB |
U AB = (5 i + 3 j + 2 k ) / 6.166
Chúng ta hãy xem xét hai vectơ 3-D u và v. Tích vô hướng của hai vectơ trong không gian 3-D được cho là:
uv = | u | | v | .cos θ
ở đâu | u | và | v | là độ lớn của hai vectơ u và v và θ là góc giữa hai vectơ.
Để hiểu khái niệm về góc giữa hai vectơ 3-D, chúng ta cùng xem lại khái niệm tích vô hướng hay tích chấm. Tích vô hướng được định nghĩa là tích của hai vectơ 3-D, mang lại một đại lượng vô hướng.
Vì vậy, góc giữa hai vectơ 3-D được cho là tích số chấm của hai vectơ chia cho tích độ lớn của hai vectơ.
Các bước sau phải được thực hiện để tính góc giữa hai vectơ 3-D:
u . v = | u | | v | .cos θ
cos θ = u . v / | u | | v |
θ = arccos ( u . v / | u | | v |)
Tương tự, góc giữa hai vectơ 3-D cũng có thể được tính bằng cách sử dụng tích chéo theo các bước tương tự như đã thảo luận ở trên, và sự khác biệt duy nhất là nó sẽ có sin thay vì cos và công thức tổng quát của tích chéo theo thứ tự hai tìm ra kết quả.
Hãy để chúng tôi hiểu khái niệm này với sự trợ giúp của một ví dụ.
Ví dụ 5
Cho biết có hai vectơ u = 2 i + 2 j + 3 k và v = 6 i + 3 j + 1 k. sử dụng công thức tích dấu chấm để tính góc giữa hai vectơ.
Giải pháp
Làm theo các bước sau để tính góc giữa hai vectơ.
θ = arccos ( u . v / | u | | v |)
Độ lớn của u được cho là,
| u | = √ ((2) ^ 2 + (2) ^ 2 + (3) ^ 2 )
| u | = √ (4 + 4 + 9)
| u | = √ (17)
Độ lớn của v được cho là,
| v | = √ ((6) ^ 2 + (3) ^ 2 + (1) ^ 2 )
| v | = √ (36 + 9 + 1)
| v | = √ (46)
Bây giờ, tính tích số chấm của hai vectơ,
uv = (2 i + 2 j + 3 k ). (6 i + 3 j + 1 k )
uv = ((2.6) (1) + (2.3) (1) + (3.1) (1))
uv = 12 + 6 +3
uv = 21
Bây giờ, bước cuối cùng, hãy đặt tất cả các giá trị vào công thức để tính giá trị của θ.
θ = arccos ( u . v / | u | | v |)
θ = arccos (21 / √ (17) .√ (46))
θ = arccos (21 / (4,12). (6,78))
θ = arccos (0,75)
θ = 0,7227 rad
Vì vậy, chuyển đổi góc thành độ,
θ = 41,36 º
Để vẽ đồ thị một vectơ 3-D, chúng ta sẽ xem xét sự tương tự sau đây.
Chúng ta hãy xem xét một hệ tọa độ 3-D với 3 trục x, y và x-trục, cũng có thể được biểu thị bằng các vectơ đơn vị tiêu chuẩn như i, j và k . Như thể hiện trong hình, các cạnh được gắn nhãn là trục x dương, trục y dương và trục z dương, và các cạnh không được gắn nhãn được coi là trục âm. Giao điểm của ba trục vuông góc được gọi là gốc tọa độ O. Vì vậy, với các trục này, điểm A bất kỳ trong không gian có thể cho ba tọa độ A = (A1, A2, A3).
Hãy xem xét một người đứng gần góc phòng và nhìn xuống điểm mà các bức tường tiếp giáp với sàn nhà. Vì vậy, giao điểm đó có thể được hình dung như một trục 3-D. Sàn và tường bên trái của người giao nhau trên một đường thẳng có thể được coi là trục x dương. Sàn và tường giao nhau về phía bên phải của người là trục y. Các bức tường giao nhau trên một đường thẳng đứng là trục z dương. Phần đối diện của mỗi trục được coi là phần âm của mỗi trục.
Một vectơ được vẽ màu xanh lam với đuôi của nó được cố định tại điểm gốc và đầu mũi tên chỉ theo hướng trong hình bên dưới. Bây giờ, vẽ hình chiếu của vectơ trên ba trục, được hiển thị bằng màu đỏ, là tọa độ của vectơ đã cho.
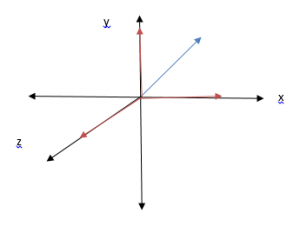

Cũng giống như trong hai chiều, chúng ta cũng có thể biểu thị một vectơ ba chiều dưới dạng vectơ đơn vị i, j và k. Đây là các vectơ đơn vị trong các trục dương trên. Một vectơ 3-D có thể bị lõm là A = A1 i + A2 j + A3 k trong đó A1, A2 và A3 là tọa độ của vectơ 3-D.
Có nhiều phần mềm vẽ và vẽ đồ thị vectơ 3-D khác nhau có thể được sử dụng để trực quan hóa và vẽ vectơ 3-D và hiểu đúng các thông số kỹ thuật của chúng.
Xem thêm:
Cách giải phương trình vectơ chuẩn theo quy định
Khám phá các thành phần Vector quan trọng nhất hiện nay