Vector là gì? Học cách vẽ vector đơn giản nhất

Vectơ truyền tải thông tin về một phần tử toán học hoặc vật lý một cách hiệu quả. Đặc biệt:

Vectơ là đại lượng toán học dùng để biểu diễn các đối tượng có cả độ lớn và hướng.

Bạn đã bao giờ tự hỏi điều gì làm cho tốc độ khác với vận tốc hoặc khối lượng khác với trọng lượng? Gợi ý: Câu trả lời liên quan đến vectơ! Chúng ta sẽ khám phá những câu hỏi này và hơn thế nữa khi chúng ta thảo luận về các chủ đề vectơ sau trong bài viết này:

• Định nghĩa vectơ
• Giới thiệu về Vectơ

Định nghĩa vectơ

Trong vật lý và toán học, một vectơ được định nghĩa là:

QUẢNG CÁO

“Một vật thể hoặc một đại lượng vật lý có thể được biểu thị bằng cả độ lớn và hướng.”

Sử dụng định nghĩa trên, chúng ta có thể thấy rằng biểu diễn của vectơ yêu cầu sự hiện diện của hai thành phần, đó là:

• Độ lớn (hoặc kích thước)
• Phương hướng

Giới thiệu về Vectơ

Trong lịch sử, vectơ được sử dụng trong hình học, vật lý và cơ học. Tuy nhiên, thời gian trôi qua, vectơ đã được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm đại số tuyến tính, kỹ thuật, khoa học máy tính, phân tích cấu trúc và điều hướng.

Vì vectơ thể hiện hai khái niệm, cụ thể là độ lớn và hướng, chúng có thể xây dựng nhiều mô hình toán học cho các vấn đề và tình huống khác nhau.

Trong phần này, chúng ta sẽ tìm hiểu về các khái niệm vectơ quan trọng sau:

• Biểu diễn Hình học và Toán học của Vectơ
• Vô hướng so với Vectơ
• Các loại Vectơ khác nhau

Biểu diễn hình học và toán học của vectơ

Các vectơ có thể được biểu diễn hình học bằng các mũi tên thẳng có độ dài cụ thể trỏ theo một hướng cụ thể với các điểm bắt đầu và kết thúc cụ thể. Chiều dài của vectơ biểu thị độ lớn của nó, trong khi hướng biểu thị hướng của nó liên quan đến một tập hợp các tọa độ. Hình ảnh dưới đây là một ví dụ về biểu diễn hình học của một vectơ.

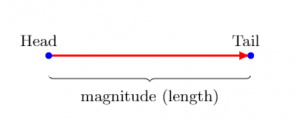
Xét hình sau đây trong đó A là một vectơ. | A | đại diện cho chiều dài (hoặc độ lớn) của nó, và đầu mũi tên chỉ từ điểm a đến điểm b thể hiện hướng của nó. Điểm a được gọi là ban đầu, hoặc bắt đầu, điểm, và điểm b được gọi là điểm đầu cuối hoặc kết thúc của vector Một . Mặc dù ví dụ này hiển thị một vectơ trong hai chiều, nó cũng có thể có ba, bốn hoặc các chiều cao hơn.

Độ lớn của vectơ về cơ bản giống với độ dài của đoạn thẳng ab. Hướng của vectơ về cơ bản giống với hướng của mũi tên.

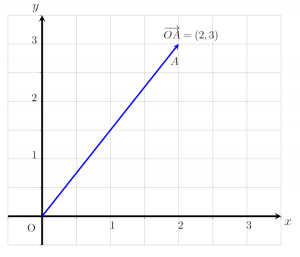
Về mặt đại số, một vectơ có thể được biểu diễn dưới dạng một cặp có thứ tự. Biểu diễn này được gọi là vectơ cột. Trong hình dưới đây, véc tơ OA được biểu diễn dưới dạng véc tơ cột.

OA = (2,3)

Điều này có nghĩa là vectơ được dịch chuyển khỏi điểm gốc bởi hai điểm dọc theo trục hoành (trục x) và bốn điểm dọc theo trục tung (trục y).

Các vectơ thường được biểu diễn bằng các chữ cái in đậm như a hoặc A.  Nếu không thể viết đậm, chẳng hạn như khi viết ghi chú bằng tay, một vectơ được biểu thị bằng một chữ cái có đầu mũi tên phía trên nó.

Vectors so với Scalars

Các đại lượng vật lý và toán học được phân loại là vectơ hoặc đại lượng vô hướng. Mặc dù chúng có liên quan với nhau, vectơ và đại lượng vô hướng được sử dụng trong các trường hợp khác nhau.

Số lượng vô hướng

Một đại lượng vô hướng có độ lớn nhưng không có hướng.

Vô hướng được biểu diễn bằng các chữ cái đơn giản như a hoặc A và chúng thường bao gồm các số thực. Một số ví dụ phổ biến về vô hướng là thời gian, tốc độ, năng lượng, khối lượng, thể tích, diện tích và chiều cao.

Số lượng vectơ

Một đại lượng vectơ vừa có độ lớn vừa có hướng.

Không giống như đại lượng vô hướng chỉ có một thành phần, đại lượng vectơ bao gồm hai thành phần. Một số ví dụ phổ biến về vectơ bao gồm vận tốc, độ dời và gia tốc.

Để hiểu rõ hơn sự khác biệt giữa đại lượng vô hướng và đại lượng vectơ, chúng ta hãy xem xét một vài ví dụ:

Nhận biết đại lượng đã cho là vectơ hay đại lượng vô hướng.

V = 10m, hướng Đông

Để phân loại đại lượng này, chúng ta cần xem xét các định nghĩa của vectơ và đại lượng vô hướng và tìm xem nó có bao nhiêu thành phần. Đầu tiên chúng ta phân tích số lượng đã cho thành các phần của nó. Đại lượng đã cho có thành phần độ lớn là | V | = 10 m. Nó cũng đang hướng về phía Đông. Do đó, chúng ta có thể kết luận rằng đại lượng đã cho là một vectơ vì nó có hai phần thành phần.

A = 5 cm

Trong ví dụ này, chỉ có thành phần độ lớn. Vì không đề cập đến hướng, đại lượng này là một đại lượng vô hướng.

Độ lớn của vô hướng A đã cho là 5 cm.

Các loại Vectơ khác nhau

Các loại vectơ khác nhau được sử dụng trong toán học bao gồm:

• Véc tơ số 0
• Vectơ đơn vị
• Vectơ bằng nhau
• Vectơ dịch chuyển
• Phủ định của một vectơ
• Vectơ vị trí
• Vectơ đồng đầu
• Vectơ Collinear
• Vectơ đồng phẳng

Mỗi loại vectơ này đều rất quan trọng và có nhiều ứng dụng khác nhau. Mô tả của họ có thể được tìm thấy dưới đây.

Véc tơ số 0

Một vectơ được gọi là vectơ không nếu độ lớn của nó bằng không. Một vectơ không bắt đầu và kết thúc tại cùng một điểm, có nghĩa là nó có tọa độ (0,0). Nó cũng không có hướng xác định. Ví dụ:  A = (0,0) và  A = 0 là các cách viết khác nhau của vectơ không.

Đơn vị véc tơ

Vectơ đơn vị là một vectơ có độ dài hoặc độ lớn bằng 1. Tìm một vectơ đơn vị có cùng hướng với một vectơ khác có thể là một công cụ hữu ích và chúng tôi gọi đây là vectơ chuẩn hóa. Một vectơ như vậy được tìm thấy bằng cách chia vectơ đã cho cho độ lớn của nó:

Y hat = Y / | Y |

Lưu ý: Hãy nhớ rằng các vectơ đơn vị chỉ bằng nhau nếu chúng cùng hướng.

Véc tơ bằng

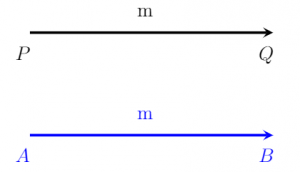
Hai hay nhiều vectơ được cho là bằng nhau nếu chúng có cùng độ lớn và cùng hướng. Hai vectơ A và B trong hình dưới đây bằng nhau vì độ lớn và hướng của chúng giống nhau.

Vector dịch chuyển

Nếu điểm X được dịch chuyển (di chuyển) từ vị trí này sang vị trí khác, Y, thì độ dời giữa hai điểm có thể được biểu diễn dưới dạng vectơ độ dời. Trong trường hợp này, vectơ độ dời sẽ được viết là XY.

Phủ định của một vectơ

Hai vectơ có cùng độ lớn nhưng ngược hướng gọi là âm của nhau. Gọi a , b là hai vectơ có cùng độ lớn. Nếu hướng của b ngược với hướng của a thì a và b là phủ định của nhau. Mối quan hệ giữa hai vectơ này là:

a = -b

Véc tơ vị trí

Vectơ vị trí được sử dụng để chỉ ra vị trí của một đối tượng trong hệ tọa độ Descartes ba chiều liên quan đến một điểm tham chiếu xác định.

Vectơ đồng đầu

Hai hay nhiều vectơ có cùng điểm đầu hoặc điểm xuất phát được gọi là vectơ đồng khởi. Trong hình cho dưới đây các vectơ, AC và AB là các vectơ đồng biến.

Vectơ Collinear

Các vectơ song song với nhau hoặc nằm trên cùng một đường thẳng được gọi là vectơ thẳng hàng.

Vectơ đồng phẳng

Hai hay nhiều vectơ ba chiều nằm trong cùng một mặt phẳng được gọi là vectơ đồng phẳng.

Các ví dụ

Trong phần này, chúng ta sẽ thảo luận về một số bài toán ví dụ vectơ và các giải pháp từng bước của chúng.

ví dụ 1

Biểu thị vectơ AD đã cho như thể hiện trong hình dưới đây dưới dạng vectơ cột.

Giải pháp

Theo định nghĩa, vectơ cột được biểu thị dưới dạng một cặp có thứ tự. Rõ ràng từ hình bên cho thấy AD bắt đầu tại điểm A và kết thúc tại điểm D. Nó được dịch chuyển 3 đơn vị về phía bên phải dọc theo trục x và 4 đơn vị hướng lên theo trục y.

Do đó, vectơ AD đã cho được viết dưới dạng vectơ cột là:

AD = (3,4)

Ví dụ 2

Biểu thị véc tơ UV đã cho như thể hiện trong hình dưới đây dưới dạng véc tơ cột.

Giải pháp

Theo định nghĩa, vectơ cột được biểu thị dưới dạng một cặp có thứ tự. Rõ ràng từ hình bên cho thấy UV bắt đầu tại điểm U và kết thúc tại điểm V. Nó bị dịch chuyển 3 đơn vị sang phải dọc theo trục x và 2 đơn vị xuống dưới dọc theo trục y.

Do đó, vectơ UV đã cho được viết dưới dạng vectơ cột là:

UV = (5, -2)

Lưu ý rằng dấu âm chỉ ra rằng chuyển động của vectơ hướng xuống dọc theo trục y.

Ví dụ 3

Xác định đại lượng đã cho dưới dạng vô hướng hoặc vectơ.

S = 40 phút

Giải pháp

Đại lượng đã cho là đại lượng vô hướng vì nó chỉ có độ lớn và không có hướng. Độ lớn của nó là | S | = 40.

Ví dụ 4

Xác định đại lượng đã cho dưới dạng vô hướng hoặc vectơ.

OW = (2, -3)

Giải pháp

Đại lượng đã cho là một vectơ. Nó được biểu diễn dưới dạng vectơ cột, OW, trong đó O là điểm đầu và W là điểm cuối. Điều này cho thấy rằng phép tịnh tiến từ O đến W là 2 điểm sang phải theo trục hoành và 3 điểm hướng xuống dọc theo trục y.

Ví dụ 5

Xác định đại lượng đã cho dưới dạng vô hướng hoặc vectơ.

V = 0

Giải pháp

Đại lượng đã cho là một vectơ. Độ lớn của vectơ V được cho là | V | = 0, vì vậy đây thực sự là một vectơ không. Do đó, hướng của vectơ này là không xác định vì vectơ 0 không có hướng.

Ví dụ 6

Xác định đại lượng đã cho dưới dạng vô hướng hoặc vectơ.

F = 20N, giảm

Giải pháp

Đại lượng đã cho là một vectơ. Độ lớn của vectơ F là | F | = 20, và hướng được đưa ra là hướng xuống.

Câu hỏi thực hành

Xác định các đại lượng sau đây là vectơ hoặc đại lượng vô hướng và xác định cả độ lớn và hướng của chúng.

1. X = 2m, hướng Bắc
2. X = 250 Kg
3. F = 20N, hướng lên
4. V = 30 m / s, hướng Tây
5. T = 20 giây
6. Y = (3,2)
7. A = 10 m / s ^ 2, theo phương thẳng đứng.
8. S = 20cm ở 60 độ
9. W = (2,5)
10. V = 20 dặm / giờ, hướng Đông Bắc
11. Biểu thị vectơ PQ đã cho như trong hình dưới đây dưới dạng vectơ cột.
12. Biểu diễn véc tơ MN đã cho như trong hình dưới đây dưới dạng véc tơ cột.

Câu trả lời

1. Vectơ: Độ lớn là | X | = 2m và hướng là hướng bắc.
2. Vô hướng: | X | = 250Kg, và chỉ độ lớn đã cho.
3. Vectơ: Độ lớn là | F | = 20N và hướng lên trên.
4. Vectơ: Độ lớn đã cho là | V | = 30 m / s và hướng là Tây.
5. Vô hướng: | T | = 20, và độ lớn duy nhất được đưa ra.
6. Vectơ: Nó là một vectơ cột trong đó 3 biểu thị 3 điểm ở bên phải dọc theo trục x và 2 biểu thị 2 điểm hướng lên dọc theo trục y. Độ lớn được cho là | Y | = sqrt (3 ^ 2 + 2 ^ 2)
7. Vectơ: Độ lớn đã cho là | A | = 10m / s ^ 2 và hướng lên trên.
8. Vectơ: Độ lớn là | S | = 20cm và phương hợp với phương một góc 60o.
9. Vectơ: Vectơ cột này di chuyển 2 điểm sang phải dọc theo trục hoành và 5 điểm lên trên theo trục tung. Độ lớn được cho là | W | = sqrt (2 ^ 2 + 5 ^ 2)
10. Vectơ: Độ lớn là | V | = 20 mph, và hướng được đưa ra là Đông Bắc.
11. Vectơ, PQ, có thể được biểu thị dưới dạng cặp có thứ tự:

PQ = (5,5).

Điều này có nghĩa là vectơ PQ bắt đầu tại điểm P và kết thúc tại điểm Q. Nó được tịnh tiến 5 điểm sang phải dọc theo trục hoành và 5 điểm lên trên.

1. Vectơ, MN, có thể được biểu diễn dưới dạng cặp có thứ tự:

MN = (-2, -4).

Điều này có nghĩa là vectơ MN bắt đầu tại điểm M và kết thúc tại điểm N. Nó được tịnh tiến 2 điểm sang trái dọc theo trục hoành và 4 điểm xuống dưới dọc theo trục y.

Xem thêm:

Cách thực hiện Vectơ trực giao chuẩn không cần chỉnh

Những thông tin cần biết về vectơ vị trí