Lý thuyết Vị trí tương đối của hai đường tròn

Sau đây là kiến thức lý thuyết Vị trí tương đối của hai đường tròn mà tintuctuyensinh đã liệt kê cho các bạn học sinh, sinh viên, các bạn có thể tham khảo dưới đây:

Vị trí tương đối của hai đường tròn

1. Các tri thức cần nhớ

Trường hợp 1: hai đường tròn (O;R)(O;R) và (O′;r)(O′;r) với (R>r)(R>r) cắt nhau

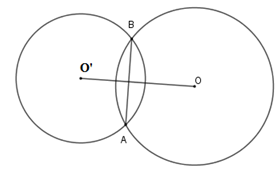
Khi đó (O)(O) và (O′)(O′) có hai điểm phổ biến và đường nối tâm là đường trung trực của đoạn ABAB.

Hệ thức liên hệ R−r<OO′<R+rR−r

Trường hợp 2: hai đường tròn xúc tiếp

+) hai đường tròn (O;R)(O;R) và (O′;r)(O′;r) với (R>r)(R>r) xúc tiếp trong tại AA.

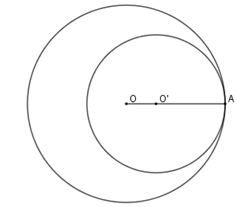
Khi đó AA nằm trên đường nối tâm và OO′=R−rOO′=R−r.

+) hai đường tròn (O;R)(O;R) và (O′;r)(O′;r) với (R>r)(R>r) tiếp xúc ngoài tại AA.

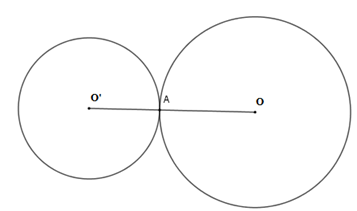
Khi đó AA nằm trên đường nối tâm và OO′=R+rOO′=R+r.

Trường hợp 3: hai đường tròn không giao nhau

+) hai đường tròn (O;R)(O;R) và (O′;r)(O′;r)(R>r)(R>r) ở ngoài nhau.

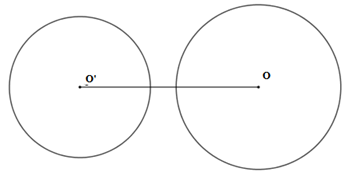
Ta có OO′>R+rOO′>R+r

+) hai đường tròn đựng nhau

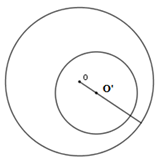
Ta có OO′<R−rOO′

+) hai đường tròn đồng tâm

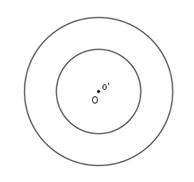
Ta có OO′=0OO′=0.

Ta có bảng sau

Đường nối tâm là trục đối xứng của hình tạo do hai đường tròn. Từ đó suy ra :

– Nếu hai đường tròn xúc tiếp nhau thì tiếp điểm nằm trên đường nối tâm.

– Nếu hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây bình thường.

2. Các dạng toán thường gặp gỡ

Dạng 1: Các bài toán có hai đường tròn xúc tiếp với nhau

Phương pháp:

sử dụng thuộc tính hai đường tròn tiếp xúc:

+ Tiếp điểm nằm trên đường nối tâm

+) Hệ thức d=R+rd=R+r

Khi làm có thể vẽ tiếp tuyến phổ biến của hai đường tròn (nếu cần)

Dạng 2: Các bài toán có hai đường tròn cắt nhau

Phương pháp:

Nối dây phổ biến của hai đường tròn rồi dùng tính chất đường nối tâm của hai đường tròn

Hệ thức hệ trọng : R−r<d<R+rR−r

Dạng 3: Các bài toán tính độ dài, diện tích

Phương pháp:

sử dụng thuộc tính đường nối tâm, thuộc tính tiếp tuyến.

sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông.