Top 7 Các Trường Đại Học Ở Đà Nẵng Uy Tín Và Tốt Nhất
27 Tháng Mười, 2020Top 7 Các Trường Đại Học Ở Đà Nẵng Uy Tín Và Tốt Nhất Con đường đến với thành...
Trong bộ môn toán hình việc nhận biết hình và tính thể tích hình đó là một bài tập rất hay được sử dụng trong các bộ đề kiểm tra. Để có được điểm cao thì đòi hỏi bạn phải tư duy và nắm chắc các công thức rất tốt. Hãy cùng tintuctuyensinh tìm hiểu ngay về HC cụt và Công thức tính thể tích hình chóp cụt qua bài viết dưới đây.
Contents
bạn đang giải bài toán ảnh hưởng tới tính thể tích hình chóp cụt nhưng mà lại chưa biết nên ứng dụng công thức nào để giải toán nhanh nhất. Vậy thì hãy theo dõi bài viết dưới đây của chúng tôi để hiểu hơn về hình chóp cụt và công thức tính thể tích hình chóp cụt.
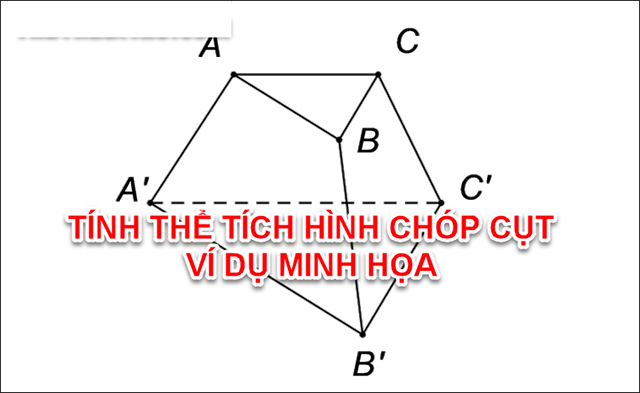
Để có thể tính được thể tích hình chóp cụt người chơi cần phải mường tượng được hình chóp cụt là như thế nào. Trong hình học không gian, hình chóp cụt là hình được tạo bởi tiết diện của một mặt phẳng song song với đáy của hình chóp.
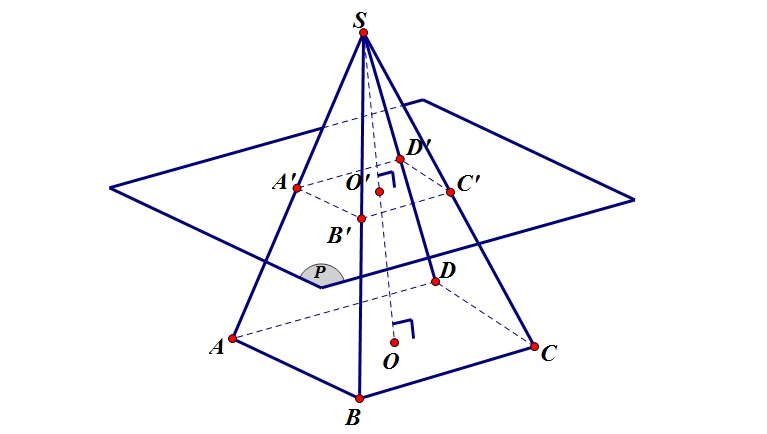

Ảnh 1: Hình chóp cụt là hình được tạo bởi vì thiết diện của một mặt phẳng đồng thời với đáy của hình chóp
Một số tính chất của hình chóp cụt:
Để tính thể tích hình chóp cụt Anh chị có thể áp dụng công thức sau:
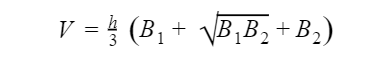
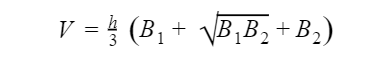
Trong đó:
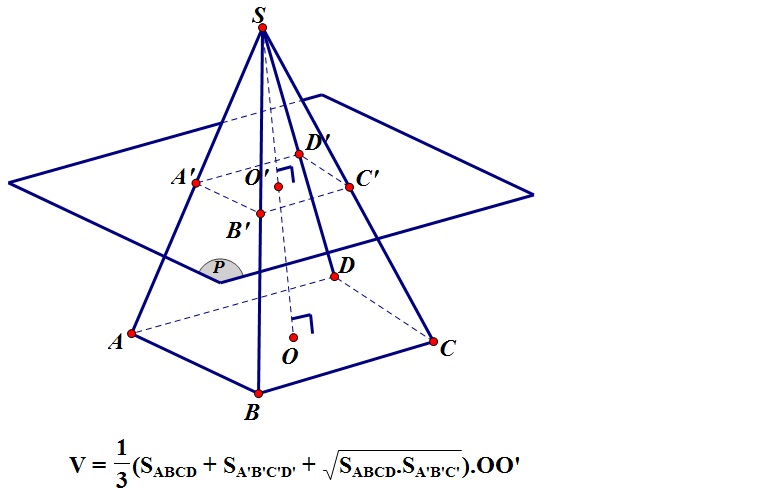

Ảnh 2: Công thức tính thể tích hình chóp cụt được ứng dụng rất phổ biến trong toán học
HC cụt là hình được tạo bởi thiết diện của một mp song song với đáy của hình chóp. Trong một HC cụt quy ước rằng đáy hình chóp chính là đáy lớn(ĐL) còn đáy nhỏ(ĐN) chính là thiết diện, những mặt còn lại chính là các mặt bên.
Đáy hình chóp có thể có nhiều hình dạng khác nhau và đáy lớn hình gì thì ta sẽ gọi đó là tên HC cụt đó.
Ví dụ ĐL hình tam giác thì ta gọi là HC cụt tam giác, đáy hình đa giác thì đó là HC cụt tứ giác,…
Một số tính chất của HC cụt mà các bạn học sinh cần nằm lòng như sau:
Các mặt bên của một HC cụt luôn là hình thang, dù hình chóp đó là HC cụt tam giác hay HC cụt tứ giác, cạnh chung của hai mặt bên kề nhau được gọi là cạnh bên.
HC cụt có một dạng đặc biệt được gọi là là HC cụt đều.
HC cụt đều chính là hình được tạo bởi thiết diện của một mp song song với đáy của hc đều. HC cụt đều là hình có tính chất đặc biệt đó là mỗi mặt bên của HC cụt đều chính là một hình thang cân.
Trên thực tế HC cụt được ứng dụng ở nhiều lĩnh vực khác nhau như:lĩnh vực đồ họa, lĩnh vực xây dựng ….

khi biết được HC cụt là gì và tính chất của nó như thế nào, ta cùng nhau nghiên cứu về CT tính thể tích HC cụt.
V = h /3 (S1+ √S1S2+ S2)
Trong công thức:
Bài tập 1: Cho HC cụt có đáy là 2 hình vuông, đáy lớn có cạnh = 7cm, đáy nhỏ cạnh = 5 cm, chiều cao hình chóp = 6 cm. Tính V của hình chóp đó.
Ta gọi DT đáy lớn HC cụt là SABCD và DTđáy bé HC cụt là SA’B’C’D’
Ta có:
SABCD = 72= 49 cm2
vì ABCD là hv với cạnh = 7 cm
A’B’C’D’ = 52= 25 cm2
vì A’B’C’D’ là hv với cạnh = 5 cm
Áp dụng công thức tính thể tích HC cụt, ta suy ra được:
V = h/3 SABCD (SABCD+ S A’B’C’D’+ S A’B’C’D’)
= 6/3 (49+ √(49 * 25) + 25)= 218 cm3.
Đáp án = 218 cm3.
Bài tập 2: Tính thể tích HC cụt biết có hai đáy là hai tam giác đều có cạnh lần lượt = 4cm và = 2cm, chiều cao của hc = 9 cm.
Giải
Với dạng bài tập này ta cần giải từng bước như sau:
phải tính DT hai đáy là hai tam giác đều.
Công thức tính S của một tam giác đều là: S = a2√3/4
Ta có:
DT đáy nhỏ: S1= 22√3/4= √3
DT đáy lớn: S2 = 423√/4 = 4 √3
Áp dụng CT tính thể tích HC cụt, ta suy ra:
V = h/3( S1+√ (S1S2)+ S2)
= 9/3 (√3+ √ (√3+ 4√3)
= 2 ( 4√3+ √ (4√3√3)+ √3) = 2 √3(4+2+1)
=14√3 cm3.
Đáp số = 14√3 cm3.
Bài tập 3: Tính thể tích của HC cụt đều ABCD.A’B’C’D có đáy lớn là hv ABCD cạnh = 6cm, đáy nhỏ hv A’B’C’D’ cạnh = 3 cm và chiều cao của HC cụt = 4cm.
Giải:
Cách giải bài tập này với các bước như sau:
Trước tiên để tính được V của hình chóp cần phải tính được S đáy lớn, S đáy bé của HC cụt. DT của 2 đáy lần lượt là:
S cuả ABCD = 6.6 = 36(cm3);S của ABCD = 6.6 = 36(cm3)
SA′B′C′D′=3.3=9(cm3)SA′B′C′D′=3.3=9(cm3)
Áp dụng CT tính thể tích HC cụt ta suy ra:
VABCD.A′B′C′D′= 43(36+căn của 36.9 + 9) = 43(36+18+9)= 84(cm3)
Vậy đáp số = 84 cm3
Bài tập 4: Cho một HC cụt đều có chiều cao = 3cm, đáy là lục giác đều, độ dài cạnh đáy = 2cm và độ dài cạnh đáy nhỏ bằng 1 cm.
Tính thể tích HC cụt ban đầu.(Vhc cụt)
Giải:
Cách giải đơn giản nhất
Gọi DT của 2 đáy hc lần lượt là S1S1, S2S2.
Ta có diện tích 2 mặt đáy lần lượt được tính là:
S(1) = 6(22√34)= 6√3 cm3
Suy ra S1= 6(2234)= 63 cm3
S2 = 6(12√34) = 3√32 cm3
Suy ra S2=6(1234)=332 cm3
Áp dụng CT tính thể tích HC cụt ta được:
V = h3 (S1+√S1S2+S2)
=33(6√3+√6√33√32+3√32)
=21√32 cm3
Chúc các bạn học tập thật tốt môn toán hình và đạt nhiều kết quả cao.
Xem thêm:
Mở bài kết bài Vợ Nhặt hay nhất 2021
Phân tích 9 câu thơ đầu bài đất nước của Nguyễn Khoa Điềm chuẩn nhất 2021
Phân tích hình tượng người lái đò trong tùy bút Người lái đò sông đà hay nhất 2021