Định lý cosin đơn giản rễ hiểu nhất 2021

Định lý cosin

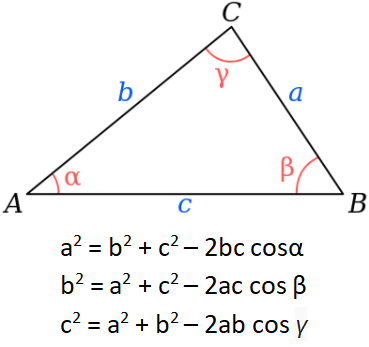
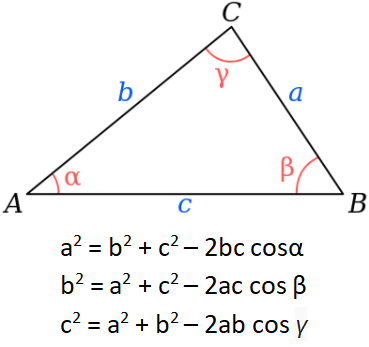
Định luật côsin , định lý cơ bản của hình học phẳng Ơclit . Định luật Cosin là một định lý toán học mô tả mối quan hệ giữa độ dài ba cạnh của một tam giác và giá trị cosin của một góc. Nó là sự tổng quát của Định lý Pitago trong trường hợp tam giác tổng quát. Định lý Pitago là một trường hợp đặc biệt của Định lý Cosine. Định luật côsin là một định lý quan trọng cho thấy mối quan hệ giữa các cạnh và góc của tam giác. Nó có thể được sử dụng trực tiếp để giải các bài toán tìm cạnh thứ ba của một tam giác đã biết với hai cạnh và góc bao gồm hoặc tìm tam giác có ba vế đã biết.Nếu định luật côsin được sửa đổi và phù hợp Việc chuyển sang kiến ​​thức khác giúp cho việc sử dụng thuận tiện và linh hoạt hơn.

Định luật cosin rất hữu ích để giải các tam giác:

Định lý này áp dụng cho bất kỳ tam giác nào:

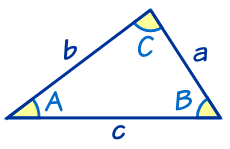một , b, và c là các cạnh của tam giác. C bên c đường chéo

Hãy lấy một ví dụ:

Ví dụ: Chiều dài của “c” là gì?

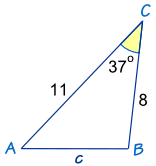
Đã biết: C = 37º, a = 8 và b = 11

Đáp số: c = 6,67

Làm sao để nhớ định lý cosin

Làm thế nào để nhớ công thức này?

Trên thực tế, công thức là Định lý Pitago để trả thêm điểm, làm cho nó phù hợp với tất cả các tam giác:

Nhớ lấy điều này:

• Hãy nghĩ về chữ cái tiếng Anh ” abc “: a ² + b ² = c ² ,
• Một ” abc ” khác: 2ab cos ( C ) ,
• Đặt lại với nhau: a ² + b ² – 2ab cos (C) = c ²

Khi nào sử dụng định lý cosin

Trong các tình huống sau, chúng ta có thể sử dụng định luật cosin:

• Cho góc giữa hai cạnh của tam giác và góc giữa hai cạnh , tìm cạnh thứ ba (như ví dụ trên)
• Biết ba cạnh của một tam giác , tìm góc (như ví dụ sau)

Ví dụ: Góc “C” lớn bao nhiêu?

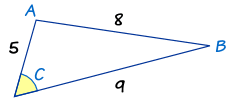
Góc đối diện của cạnh có độ dài “8” là C nên cạnh này là c . Hai vế còn lại là a và b .

Thay giá trị đã biết vào định luật cosin :

Các chứng từ khác định lý cosin

Dạng tìm góc đơn giản định lý cosin

Trên đây chúng ta đã xem cách tìm góc của ba cạnh đã biết. Chúng tôi đã thực hiện một vài bước để làm điều đó, nhưng công thức “trực tiếp” thực tế sẽ đơn giản hơn (công thức chỉ là sự sắp xếp lại của công thức: c ² = a ² + b ² – 2ab cos (C) ). Công thức có thể có ba dạng:

cos (C) = a ² + b ² – c ²2ab

cos (A) = b ² + c ² – a ²2bc

cos (B) = c ² + a ² – b ²2ca

Ví dụ: Sử dụng định luật côsin (dạng góc) để tìm góc “C”

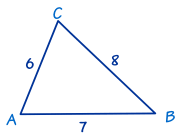
Ba mặt đã biết:

• a = 8,
• b = 6 và
• c = 7.

Sử dụng định luật côsin (dạng góc) để tìm góc C :

dạng của a, b và c

Bạn cũng có thể ghi đè C ² = A ² + B ² – của 2AB COS (C) công thức ” A ² = ” và ” B ² = “.

Sau đây là ba hình thức:

Nhưng cách dễ nhất là nhớ dạng ” c ² =” và sử dụng các chữ cái khác nhau khi áp dụng!

như sau:

Ví dụ: Tìm độ dài “z”

Các chữ cái khác nhau! Ổn mà. Chúng ta có thể thay x cho a, y cho b và z cho c

Đáp số: z = 14,5

Chú ý rằng cos (131º) là âm? Điều này biến dấu hiệu cuối cùng thành dấu + (dương). Tính cosin góc bắt buộc phải âm (xem hình tròn đơn vị ).

Xem thêm bài viết: