TÂM ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC CHUẨN VÀ RỄ HỌC NHẤT

Trong môn Toán 9, người học cần nắm được ĐT, đặc biệt là đường tròn ngoại tiếp tam giác. Từ sự quan trọng của lý thuyết này, Tuvantuyensinh hiểu được điều đó nên đã tổng hợp những kiến ​​thức bổ ích cho người học. đường tròn ngoại tiếp tam giác là gì? Công thức tính bán kính, tìm được tâm đường tròn ngoại tiếp tam giác,… sẽ có trong bài viết dưới đây

1. Khái niệm đường tròn ngoại tiếp tam giác

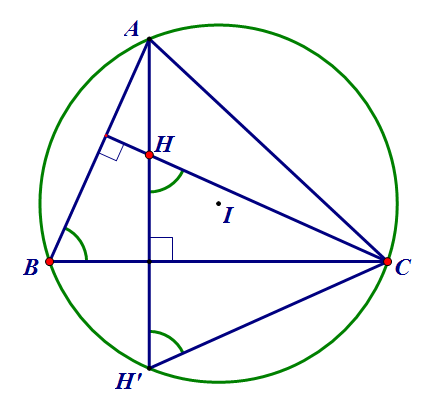
– đường tròn ngoại tiếp tam giác là một ĐT được vẽ mà nó đi qua 3 đỉnh của TG đã cho sẵn. Nói cách khác, TG nằm trong ĐT hay nội tiếp ĐT

– Ví dụ về đường tròn ngoại tiếp tam giác:

Đường phân giác trung trực của đoạn thẳng EG là đường thẳng đi qua trung điểm M của EG, vuông góc với EG. Mọi điểm I trên đoạn thẳng EG đều có IE = IG.

Ba đường phân giác vuông góc đồng quy tại một điểm. Gọi I là giao điểm của ba đường trung trực của TG ABC thì ta có IA = IB = IC, I là tâm ĐT ngoại tiếp TG ABC. ĐT ngoại tiếp TG là ĐT đi qua 3 đỉnh của TG đã cho.

– Cách vẽ ĐT ngoại tiếp TG (xem theo hình vẽ)

Khái niệm và tính chất của tâm đường tròn ngoại tiếp tam giác.

2. Giao điểm của đường tròn ngoại tiếp tam giác là gì?

– Tâm ĐT ngoại tiếp TG là giao điểm của ba đường phân giác của ba cạnh vuông góc (có thể là giao điểm của hai đường phân giác vuông góc).

– Cách xác định tâm ĐT ngoại tiếp TG:

Xác định tâm ĐT ngoại tiếp TG

Xác định tâm ĐT ngoại tiếp TG

+ Phương án 1:

Bước 1: Viết PT các đường trung trực của một TG bất kỳ.

Bước 2: Tìm giao điểm của hai đường phân giác vuông góc với nhau là tâm ĐT ngoại tiếp TG.

+ Cách 2:

Bước 1: Gọi I (x, y) là tâm ĐT ngoại tiếp TG ABC. Ta có YA = YB = YC bằng R.

Bước 2: Tìm tọa độ tâm ĐT ngoại tiếp TG:

 Tọa độ tâm I là nghiệm của PT cần tìm:

Tâm ĐT ngoại tiếp TG cân ABC tại A nằm trên đường cao AH.

Tâm ĐT ngoại tiếp TG vuông là trung điểm của cạnh huyền.

Tâm ĐT ngoại tiếp TG là trọng tâm của TG.

3. Bán kính đường tròn ngoại tiếp tam giác

Ngoài các công thức liên quan đến ĐT, các em cần biết thêm công thức tính bán kính ĐT ngoại tiếp TG.

Bán kính ĐT ngoại tiếp TG

Bán kính ĐT ngoại tiếp TG

Cho TG ABC. Các cạnh BC, AC, AB có thứ tự được đặt là a, b, c.

– Công thức tính bán kính ĐT ngoại tiếp TG

+ Công thức tính diện tích TG (áp dụng công thức heng):

+ Nửa chu vi hình TG:

+ Công thức tính bán kính ĐT nội tiếp TG:

– Công thức tính bán kính ĐT ngoại tiếp góc A:

– Công thức tính bán kính ĐT ngoại tiếp góc B:

– Công thức tính bán kính ĐT ngoại tiếp góc C:

– Công thức tính bán kính ĐT ngoại tiếp TG đều

4. Bài tập tìm tâm đường tròn ngoại tiếp tam giác

Tìm tọa độ tâm đường tròn ngoại tiếp tam giác trong các trường hợp sau:

Tại mp Oxy cho TG DEF với A ( 5 ; 7 ) ; B ( 2 ; 9 ) ; C ( – 2 ; – 1 )

Tại mp Oxy cho 3 điểm với A ( – 5 ; – 7 ) ; B ( 5 ; – 9 ) ; C ( 2 ; 1 )

Cho DT (O) đi qua ba điểm A ; B và C. Lập PT ĐT đi qua 3 điểm:

+ Bước 1: Gọi phương trình của đường tròn là (C): x2 + y2 – 2ax – 2by + c = 0 (*)

(với ĐK a2 + b2 – c > 0).

+ Bước 2: Ta có điểm A; B và C được nằm trên một ĐT nên khi bỏ số liệu c tọa độ điểm A; B, C vào (*) ta được phương trình ba ẩn a; b; c.

+ Bước 3: giải hệ phương trình ba ẩn a; b; c ta được phương trình của đường tròn.

1. Ví dụ minh họa

Ví dụ 1: Tâm đường tròn qua ba điểm A (2; 1); B (2; 5) và C (-2; 1) thuộc đường thẳng có phương trình

3.     x – y + 2 = 3.
4.     x + y – 3 = 0
5.     x – y – 3 = 0
6.     x + y + 3 = 0

Hướng dẫn giải pháp

Phương trình đường tròn (C) có dạng:

x2 + y2 – 2by + c – 2ax = 0 (a2 + b2 – c> 0)

Viết PT ĐT tròn được đi qua 3 điểm (ĐT ngoại tiếp TG) ⇒ I (0; 3)

Vậy tâm của đường tròn là I (0; 3).

Lần lượt thay tọa độ I cho các phương trình tuyến tính, chỉ có đường thẳng

x – y + 3 = 0 thỏa mãn.

Chọn Phương án A.

Ví dụ 2. Tìm tọa độ tâm đường tròn đi qua 3 điểm A (0; 4); B (2; 4) và C (4; 0)

1. (0; 0) B. (1; 0) C. (3; 2) D. (1; 1)

Hướng dẫn giải pháp

Phương trình đường tròn (C) có dạng:

x2 + y2 – 2ax – 2by + c = 0 (a2 + b2 –c> 0)

Do 3 điểm A; B; C thuộc (C) nên Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác) | Tuyển chọn các bài giải bài tập Toán lớp 10 có đáp án

Vì vậy, tâm tôi (1; 1)

Chọn D.

Xem thêm:

GIẢI MÃ: KHỐI C GỒM NHỮNG NGÀNH NÀO?

Những Ai Nên Học Ngành Kỹ Thuật Điện – Reviews Chi Tiết

HỌC CÁC NGÀNH KHỐI C CÓ DỄ XIN VIỆC LÀM KHÔNG?