3 4 5 Hình tam giác vuông là gì và cách giải chi tiết nhất

Hình tam giác vuông rất hữu ích trong cuộc sống hàng ngày của chúng ta. Kích thước của tam giác vuông càng đơn giản thì cách sử dụng của nó càng đơn giản.

Các khả năng nhận tam giác đặc biệt đúng là các phím tắt để giải quyết các vấn đề liên quan đến tam giác vuông. Thay vì sử dụng định lý Pitago, bạn có thể chỉ cần sử dụng các tỷ lệ của một tam giác vuông đặc biệt để tính độ dài còn thiếu.

Chúng có thể có các kích thước khác nhau nhưng phổ biến nhất là tam giác vuông 3-4-5 . Trong bài này, chúng ta sẽ tìm hiểu tam giác vuông 3-4-5 là gì và cách giải các bài toán liên quan đến tam giác vuông 3-4-5.

Trong hình học, tam giác là một đa giác hai chiều có ba góc, ba đỉnh và ba góc ghép với nhau tạo thành một sơ đồ khép kín. Có nhiều loại hình tam giác khác nhau tùy thuộc vào độ dài các cạnh và độ lớn của các góc trong của chúng. Để biết thêm chi tiết về hình tam giác, bạn có thể xem qua các bài viết trước.

Tam giác vuông 3-4-5 là gì?

Tam giác vuông 3-4-5 là tam giác có độ dài các cạnh theo tỷ lệ 3: 4: 5. Nói cách khác, một tam giác 3-4-5 có tỉ số các cạnh là số nguyên được gọi là Tam giác Pitago

Tỷ lệ này có thể được đưa ra là:

Mặt 1: Mặt 2: Hypotenuse = 3n: 4n: 5n = 3: 4: 5

Chúng ta có thể chứng minh điều này bằng cách sử dụng Định lý Pitago như sau:

⇒ a ²  + b ²  = c ²

⇒ 3 ² + 4 ² = 5 ²

⇒ 9 + 16 = 25

25 = 25

Một tam giác vuông 3-4-5 có ba góc trong là 36,87 °, 53,13 ° và 90 °. Do đó, tam giác vuông 3 4 5 có thể được xếp vào loại tam giác vô hướng vì độ dài ba cạnh và góc trong của nó đều khác nhau

Hãy nhớ rằng tam giác 3-4-5 không có nghĩa là tỷ lệ chính xác là 3: 4: 5, mà nó có thể là bất kỳ nhân tố chung nào của những con số này. Ví dụ, một tam giác 3-4-5 cũng có thể có các dạng sau:

• 6-8-10
• 9-12-15
• 12-16-20
• 15-20-25

Cách giải Tam giác 3-4-5

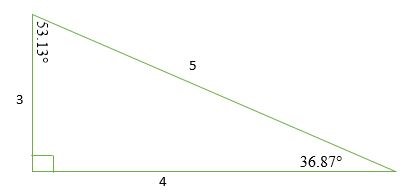
Giải một tam giác vuông 3-4-5 là quá trình tìm độ dài các cạnh còn thiếu của tam giác. Tỷ lệ 3: 4: 5 cho phép chúng ta nhanh chóng tính toán các độ dài khác nhau trong các bài toán hình học mà không cần dùng đến các phương pháp như sử dụng bảng hoặc định lý Pythagoras.

ví dụ 1

Tìm độ dài một cạnh của tam giác vuông trong đó cạnh huyền và cạnh kia lần lượt là 30 cm và 24 cm.

Giải pháp

Kiểm tra tỷ lệ để xem nó có phù hợp với 3n: 4n: 5n không

?: 24: 30 =?: 4 (6): 5 (6)

Đây phải là một tam giác vuông 3-4-5, vì vậy chúng ta có;

n = 6

Do đó chiều dài của cạnh còn lại là;

3n = 3 (6) = 18 cm

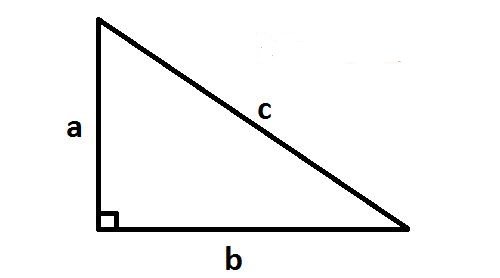
Ví dụ 2

Cạnh dài nhất và cạnh đáy của buồm hình tam giác của thuyền buồm lần lượt là 15 thước và 12 thước. Cánh buồm cao bao nhiêu?

Giải pháp

Kiểm tra tỷ lệ

⇒ ?: 12: 15 =? : 4 (3): 5 (3)

Do đó, giá trị của n = 3

Người thay thế.

⇒ 3n = 3 (3) = 9

Do đó, chiều cao của cánh buồm là 9 thước Anh.

Ví dụ 3

Xác định tam giác vuông 3-4-5 từ danh sách các tam giác sau

1. Tam giác A ⇒ 8, 8, 25
2. Tam giác B ⇒ 9, 12, 15
3. Tam giác C ⇒ 23, 27, 31
4. Tam giác D ⇒ 12, 16, 20
5. Tam giác E ⇒ 6, 8, 10

Giải pháp

Kiểm tra tỉ số của mỗi tam giác.

A ⇒ 8: 8: 25

B ⇒ 9: 12: 15 (chia mỗi số hạng cho 3)

= 3: 4: 5

C ⇒23: 27: 31

D ⇒ 12: 16: 20 (chia mỗi số hạng cho 4)

= 3: 4: 5

E ⇒ 6: 8: 10 (chia hết cho 2)

= 3: 4: 5

Do đó, các tam giác B, D và E là 3-4-5 tam giác vuông.

Xem thêm: 

Tam giác 30-60-90 là gì? Hướng dẫn cách giải hay nhất

Tam giác 45 ° -45 ° -90 ° là gì? Hướng dẫn cách giải đơn giản nhất

Ví dụ 4

Tìm giá trị của x trong hình vẽ bên. Giả sử tam giác là 3-4-5 tam giác vuông.

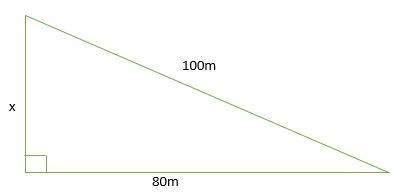
Giải pháp

Tìm thừa số “n” trong tam giác vuông 3-4-5.

?: 80: 100 =?: 4 (20): 5 (20)

Do đó, n = 20

Thay thế trong 3n: 4n: 5n.

3n = 3 (20) = 60

Do đó, x = 60 m

Ví dụ 5

Tính độ dài đường chéo của một tam giác vuông với độ dài các cạnh là 6 inch và 8 inch.

Giải pháp

Kiểm tra tỷ lệ nếu nó phù hợp với tỷ lệ 3n: 4n: 5n.

6: 8 😕 = 3 (2): 4 (2):?

n = 2

Thay n = 2 vào 5n.

5n = 5 (2) = 10.

Do đó, chiều dài của đường chéo là 10 inch.