Tam giác
Hình phẳng đóng, có ba cạnh và ba góc được gọi là hình tam giác.
Các loại tam giác:
Dựa vào các cạnh – a) Bằng nhau b) Cân c) Tính vô hướng
Dựa vào các góc – a) Tam giác vuông cân b) Tam giác vuông c) Tam giác vuông cân
Để biết thêm thông tin về hình tam giác, hãy xem video bên dưới.
Diện tích hình tam giác
A r e a = (1/2) × b a s e × h e i g h t
Trong trường hợp tam giác đều và tam giác cân, nếu độ dài các cạnh của tam giác đã cho thì ta sử dụng định lý Pythagoras để tìm chiều cao của tam giác.
Diện tích tam giác đều
Xét một Δ A B C cạnh đều, với mỗi cạnh là một đơn vị. Gọi AO là tia phân giác BC. Để suy ra công thức về diện tích của một tam giác đều, chúng ta cần tìm chiều cao AO.
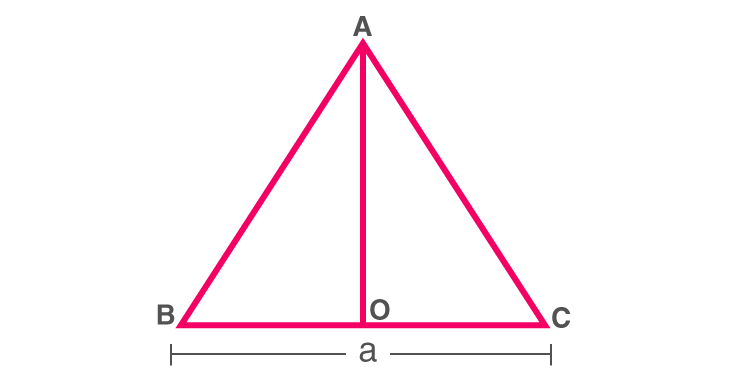

Sử dụng định lý Pythagoras,
A C 2 = O A 2 + O C 2
O A 2 = A C 2 – O C 2
Thay A C = a , O C = a / 2 vào phương trình trên.
O A 2 = một 2 – một 2 /4
O Một = √3a / 2
Ta biết rằng diện tích tam giác là:
A = (1/2) × b a s e × h e i g h t
A = (1/2) × a × (√3a / 2)
∴ Một r e một o f E q u i l một t e r một l t r i một n g l e = √3a 2 /4
Diện tích tam giác cân
Xét một hình cân bằng Δ A B C có các cạnh bằng nhau là một đơn vị và cơ sở là b đơn vị.


Tam giác cân ABC
Chiều cao của tam giác có thể được tìm thấy bằng Định lý Pythagoras:
C D 2 = A C 2 – A D 2
⇒ h 2 = a 2 – (b 2/4 ) = (4 a 2 – b 2 ) / 4
⇒ h = (1/2) √ (4 a 2 – b 2 )
Diện tích tam giác là A = (1/2) b h
∴ A = (1/2) × b × (1/2) √ (4 a 2 – b 2 )
∴ A = (1/4) × b × √ (4 a 2 – b 2 )
Diện tích tam giác – Theo công thức Heron
Diện tích của Δ A B C , các cạnh a, b, c cho trước theo công thức Heron (còn gọi là công thức Hero) là:


Tam giác ABC
Tìm (s) nửa chu vi = (a + b + c) / 2
A r e a = √ [s (s – a) (s – b) (s – c)]
Công thức này rất hữu ích để tìm diện tích của một tam giác vô hướng, với độ dài của tất cả các cạnh của nó.
Để biết thêm về Công thức của Heron, hãy truy cập vào đây .
Diện tích của một đa giác bất kỳ – Theo công thức Heron
Đối với một tứ giác, khi một trong các giá trị đường chéo và các cạnh của nó đã cho, thì diện tích có thể được tính bằng cách tách tứ giác đã cho thành hai tam giác và sử dụng công thức Heron.
Ví dụ : Một công viên có dạng tứ giác ABCD có ∠ C = 90 ∘ , AB = 9 cm, BC = 12 cm, CD = 5 cm và AD = 8 cm. Nó chiếm bao nhiêu diện tích?
⇒ Ta vẽ hình theo thông tin đã cho.
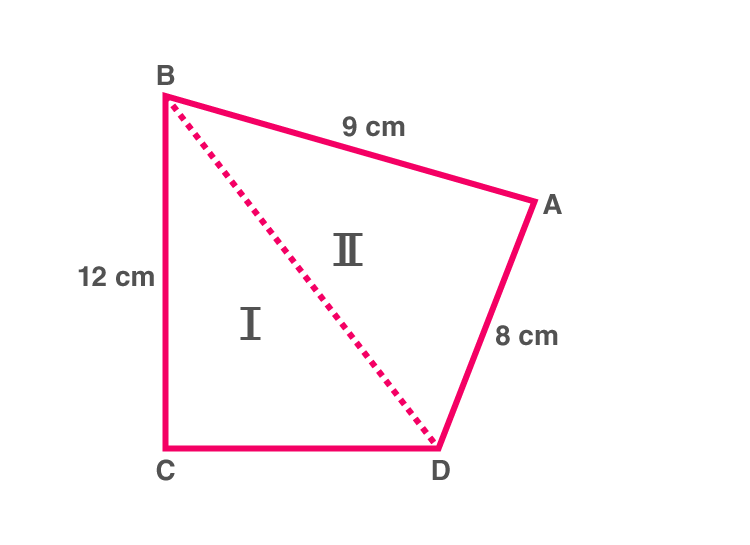

Hình có thể tách thành 2 tam giác Δ B C D a n d Δ A B D
Từ ∆ B C D , ta có thể tìm được BD (Sử dụng định lý Pythagoras)
B D 2 = 12 2 + 5 2 = 169
B D = 13 c m
Bán chu vi cho Δ B C D S 1 = (12 + 5 + 13) / 2 = 15
Nửa chu vi Δ A B D S 2 = (9 + 8 + 13) / 2 = 15
Sử dụng công thức của Heron A 1 a n d A 2 sẽ là:
A 1 = √ [15 (15 – 12) (15 – 5) (15 – 13)]
A 1 = √ (15 × 3 × 10 × 2)
A1 = √900 = 30 cm2
Tương tự,
A 2 sẽ là35,49 c m 2 .
Diện tích tứ giácABCD = A 1 + A 2 = 65,49c m 2
Xem thêm: