Bất đẳng thức tam giác là gì và những ví dụ điển hình nhất

Trong bài này, chúng ta sẽ tìm hiểu định lý bất đẳng thức tam giác là gì, cách sử dụng định lý và cuối cùng, bất đẳng thức tam giác ngược bao gồm những gì. Tại thời điểm này, hầu hết chúng ta đã quen thuộc với thực tế là một tam giác có ba cạnh.

Các ba mặt của một hình tam giác được hình thành khi ba đoạn thẳng khác nhau tham gia vào các đỉnh của một tam giác. Trong một tam giác, w e sử dụng các chữ cái nhỏ a, b và c để biểu thị các cạnh của một tam giác .

Trong hầu hết các trường hợp, chữ a và b được dùng để biểu thị hai cạnh ngắn đầu tiên của tam giác, trong khi chữ c được dùng để biểu thị cạnh dài nhất .

Định lý Bất đẳng thức Tam giác là gì?

Như tên cho thấy, định lý bất đẳng thức tam giác là một phát biểu mô tả mối quan hệ giữa ba cạnh của một tam giác. Theo định lý bất đẳng thức tam giác, tổng hai cạnh bất kỳ của tam giác lớn hơn hoặc bằng cạnh thứ ba của tam giác.

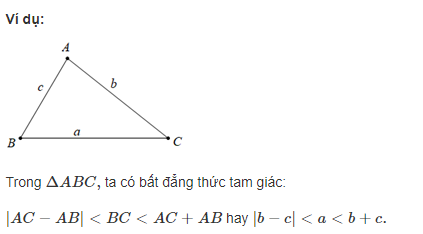
Câu lệnh này có thể được biểu thị bằng;

• a + b> c
• a + c> b
• b + c> a

Do đó, định lý bất đẳng thức tam giác là một công cụ hữu ích để kiểm tra xem một bộ ba kích thước đã cho có tạo thành một tam giác hay không . Nói một cách dễ hiểu, một tam giác sẽ không được tạo thành nếu 3 điều kiện bất đẳng thức tam giác trên là sai.

Hãy xem các ví dụ sau:

ví dụ 1

Kiểm tra xem có thể tạo thành một tam giác hay không bằng các biện pháp sau:

4 mm, 7 mm và 5 mm.

Giải pháp

Cho a = 4 mm. b = 7 mm và c = 5 mm. Bây giờ áp dụng định lý bất đẳng thức tam giác.

a + b> c

⇒ 4 + 7> 5

⇒ 11> 5 ……. (thật)

a + c> b

⇒ 4 + 5> 7

⇒ 9> 7 …………. (thật)

b + c> a

⇒7 + 5> 4

⇒ 12> 4 ……. (thật)

Vì cả ba điều kiện đều đúng nên có thể tạo thành một tam giác với các số đo đã cho.

Ví dụ 2

Đưa ra các số đo; 6 cm, 10 cm, 17 cm. Kiểm tra xem ba số đo có thể tạo thành một tam giác không.

Giải pháp

Cho a = 6 cm, b = 10 cm và c = 17 cm

Theo định lý bất đẳng thức tam giác, ta có;

a + b> c

⇒ 6 + 10> 17

⇒ 16> 17 ………. (sai, 17 không nhỏ hơn 16)

a + c> b

⇒ 6 + 17> 10

⇒ 23> 10 …………. (thật)

b + c> a

10 + 17> 6

17> 6 ………. (thật)

Vì một trong các điều kiện là sai, do đó, ba số đo không thể tạo thành một tam giác.

Ví dụ 3

Tìm các giá trị có thể có của x đối với tam giác dưới đây.

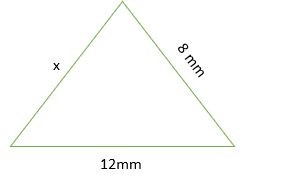
Giải pháp

Sử dụng định lý bất đẳng thức tam giác, ta được;

⇒ x + 8> 12

⇒ x> 4

⇒ x + 12> 8

⇒ x> –4 ……… (không hợp lệ, độ dài không bao giờ được là số âm)

12 + 8> x

⇒ x <20 Kết hợp các câu lệnh hợp lệ x> 4 và x <20.

4 <x <20

Do đó, các giá trị có thể có của x là; 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 và 19.

Ví dụ 4

Kích thước của một tam giác là (x + 2) cm, (2x + 7) cm và (4x + 1). Tìm các giá trị có thể có của x là số nguyên.

Giải pháp

Bằng định lý bất đẳng thức tam giác; cho a = (x + 2) cm, b = (2x + 7) cm và c = (4x + 1).

(x + 2) + (2x + 7)> (4x + 1)

3x + 9> 4x + 1

3x – 4x> 1 – 9

– x> – 8

Chia cả hai vế cho – 1 và đảo ngược hướng của biểu tượng bất đẳng thức.

x <8 (x + 2) + (4x +1)> (2x + 7)

5x + 3> 2x + 7

5x – 2x> 7 – 3

3x> 4

Chia cả hai vế cho 3 để được;

x> 4/3

x> 1,3333.

(2x + 7) + (4x + 1)> (x + 2)

6x + 8> x + 2

6x – x> 2 – 8

5x> – 6

x> – 6/5 …………… (không thể)

Kết hợp các bất đẳng thức hợp lệ.

1,333 <x <8

Do đó, các giá trị nguyên có thể có của x là 2, 3, 4, 5, 6 và 7.

Ví dụ 5:

Tìm các giá trị có thể có của x để tam giác có độ dài các cạnh là 10, 7, x

Giải pháp:

Độ dài đã cho là 10 và 7.

Chênh lệch độ dài = 10 – 7 = 3

Tổng chiều dài = 10 + 7 = 17

Do đó, các giá trị có thể có của x nằm trong khoảng;

3 <x <17

Xem thêm:

Tam giác 30-60-90 là gì? Hướng dẫn cách giải hay nhất

Tam giác 45 ° -45 ° -90 ° là gì? Hướng dẫn cách giải đơn giản nhất

Bất đẳng thức tam giác ngược

Theo bất đẳng thức tam giác ngược, hiệu số giữa độ dài hai cạnh bất kỳ của tam giác nhỏ hơn độ dài cạnh thứ ba . Nói cách khác, bất kỳ cạnh nào của tam giác đều lớn hơn số trừ thu được khi trừ hai cạnh còn lại của tam giác.

Xét tam giác PQR dưới đây;

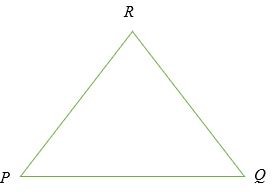
Định lý bất đẳng thức tam giác ngược được cho bởi;

| PQ |> || PR | – | RQ ||, | PR |> || PQ | – | RQ || và | QR |> || PQ | – | PR ||

Bằng chứng:

• | PQ | + | PR | > | RQ | // Định lý bất đẳng thức tam giác
• | PQ | + | PR | – | PR | > | RQ | – | PR | // (i) Trừ một lượng giống nhau cho cả hai vế duy trì sự bất bình đẳng
• | PQ | > | RQ | – | PR | = || PR | – | RQ || // (ii), các thuộc tính của giá trị tuyệt đối
• | PQ | + | PR | – | PQ | > | RQ | – | PQ | // (ii) Trừ một lượng giống nhau cho cả hai vế duy trì bất đẳng thức
• | PR | > | RQ | – | PQ | = || PQ | – | RQ || // (iv), các thuộc tính của giá trị tuyệt đối
• | PR | + | QR | > | PQ | // Định lý bất đẳng thức tam giác
• | PR | + | QR | – | PR | > | PQ | – | PR | // (vi) Trừ một lượng giống nhau cho cả hai vế duy trì bất đẳng thức
• | QR | > | PQ | – | PR | = || PQ | – | PR || // (vii), thuộc tính có giá trị tuyệt đối.

Vấn đề thực hành:

1. Phát biểu nếu các số cho dưới đây có thể là số đo ba cạnh của một tam giác.

7, 13 và 4

2. Hai cạnh của một tam giác có số đo là 10 và 11. Xác định các giá trị có thể có của cạnh còn lại của tam giác đó.
3. Tìm dãy các số đo có thể có của x trong các cạnh cho trước của tam giác:

11, 10, x

4. Phát biểu nếu ba số cho dưới đây có thể là số đo các cạnh của một tam giác.

6, 12 và 3

5. Hai cạnh của một tam giác có số đo là 9 và 10. Tính các giá trị có thể có của cạnh còn lại của tam giác đó.