Cách lập bảng biến thiên của hàm số

Đây cũng là dạng bài tập vững chắc sẽ gặp gỡ trong các bài kiểm tra, bài thi cần thiết của môn Toán. Các học sinh không chỉ nên nắm vững lý thuyết mà còn cần chắc phần thực hành, ứng dụng vào các bài tập một cách thuần thục. Bài viết sau đây sẽ nêu lên thí dụ bài tập khảo sát hàm số bất kì qua các bước chi tiết. Hãy cùng tò mò và khám phá.

Khảo sát hàm số

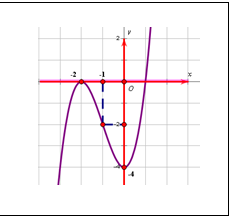
thí dụ 1: Khảo sát hàm số y = x³ + 3x² – 4.

Tìm tập xác định

Tập xác định: D=R

Tìm nghiệm của hàm số

1. Cách giải phương trình bậc nhị

Để tìm nghiệm của hàm số, cần nắm cách giải phương trình bậc nhị như sau:

• Phương trình bậc nhì là phương trình có dạng ax² + bx + c = 0

• Với a ≠0
• a,b,c là các hằng số
• x là ẩn số

• Cách giải phương trình bậc hai:

• Định lý Vi-et thuận về nghiệm của phương trình bậc 2

nhị số x¹, x² là nghiệm của phương trình ax² + bx = c = 0 khi và chỉ khi

x1 + x2 =-bax1.x2 =ca

• Định lý Viet đảo về nghiệm của phương trình bậc 2

Nếu có 2 số u, v có u + v = S và u.v = P thì u và v là nghiệm của phương trình:

X² – SX + P = 0.

1. Tìm nghiệm của hàm số theo hệ trục tọa độ: trục Ox, Oy

y’ = 3x² + 6x

y’ = 0

⬄ 3x² + 6x = 0

⬄ x(3x + 6) = 0

⬄ x = 0 và x = -2

Giao điểm với Ox: y = 0 => x = -2; x = 1

Giao điểm với Oy: x = 0 => y = -4

Giới hạn : lim y x→+∞= +∞ ; lim y x→-∞= -∞

Bảng biến thiên

1. Lý thuyết về bảng biến thiên

• Định nghĩa: Kí hiệu K là một khoảng, nửa khoảng hoặc một đoạn
  • Hàm số f(x) được gọi là đồng biến trên K, nếu với mọi cặp x₁, x₂ ϵ K nhưng mà x₁ < x₂ thì f(x₁) < f(x₂)
  • Hàm số f(x) được gọi là nghịch biến trên K, nếu với mọi cặp x1, x2 ϵ K mà x1 < x2 thì f(x1) > f(x2)
  • Hàm số f(x) đồng biến (nghịch biến) trên K còn gọi là tăng (hay giảm ) trên K. Hàm số đồng biến hoặc nghịch biến trên K còn gọi chung là hàm số đơn điệu trên K.
• Định lý

Cho hàm số y = f(x) xác định và có đạo hàm trên K

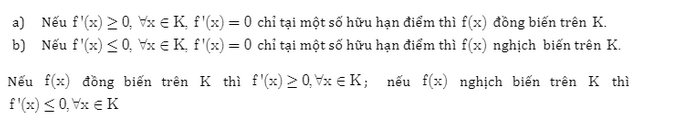
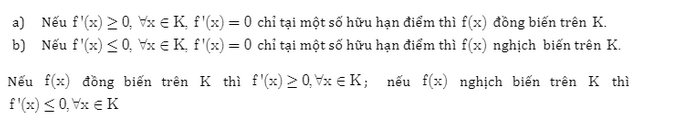
Định lý về dấu tam thức bậc hai

1. Vẽ bảng biến thiên để tìm các điểm của đồ thị hàm số

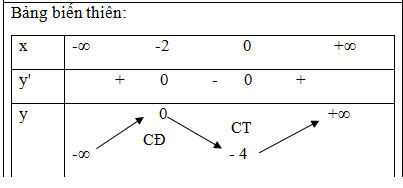
Điểm cực đại: x = -2, y = 0

Điểm cực tiểu: x = 0, y = -4

Đạo hàm cấp 2: y’’ = 6x + 6

y’’ = 0 ⬄ 6x + 6 = 0 ⬄ x=1

Điểm uốn I (1;-2)

Vẽ đồ thị

Trên đây là những bước giải bài tập khảo sát và vẽ đồ thị hàm số cụ thể nhất. chờ đợi bài viết đã cung ứng cho game thủ những tri thức hữu ích. game thủ có thể khám phá về các kiến thức học tập khác trên VOH.